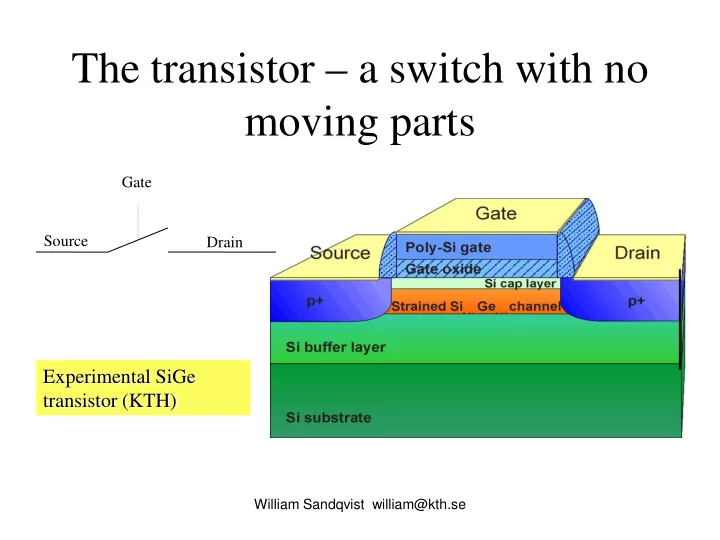
The transistor a switch with no moving parts Gate Source Drain - PowerPoint PPT Presentation

The transistor – a switch with no moving parts Gate Source Drain Experimental SiGe transistor (KTH) William Sandqvist william@kth.se

Why CMOS? • CMOS-Transistors are easy to manifacture • CMOS-Transistors are made of ordinary sand => cheap raw materials • A transistor is easy to get to work as a switch William Sandqvist william@kth.se

P and N MOS-transistors ”Pull Up” ”Pull Down” 1 0 William Sandqvist william@kth.se

The structure of a CMOS-circuit Two different circuits: PMOS makes the output ”1” NMOS makes the output ”0” William Sandqvist william@kth.se

Inverter V DD A CMOS-circuit consists of both PMOS and NMOS circuits. The acronym CMOS stands for T 1 (Complementary MOS). V V x f T 1 T x f 2 T 2 0 on off 1 1 off on 0 (a) Circuit (b) Truth table and transistor states Area: A inverter = 2 Transistors William Sandqvist william@kth.se

CMOS-inverter voltage levels Uotput voltage V f V DD ”1” T 1 V V x f T 2 ”0” ”0” ”1” Input voltage V x William Sandqvist william@kth.se

Typical signal-levels for CMOS Utput voltages V O and input voltges V I fits together like "hand in a glove", and with a margin to! V Hmax V OHmin V IHmin V ILmax V OLmax V Lmin Margins! William Sandqvist william@kth.se

One point is unstable ! • CMOS-circuit has a very stable transfer function V out • At V in =V DD /2 there is an unstable unstable point, when both T 1 and T 2 is VDD conducting. • If a circuit temporarily stuck in this mode, it enters a state called metastability. V in • If this condition lasts for a long time VDD then the transistors in the circuit can be damaged by the high current. Unstable point We will return to metastability ... William Sandqvist william@kth.se

CMOS - Dynamic losses ! Classical CMOS has only losses exactly at the vid switching point . The Powerdissipation P F is proportional to the clock- frequency! f ”1” → ”0” C ”1” ← ”0” ⋅ 2 f C ∝ ⋅ 2 ”1” ”0” P f V F C DD P Power losses F f Clockfrequ ency C V Supply Voltage DD William Sandqvist william@kth.se

NAND-gate V DD V A V B V OH V OH V SS (0) V SS (0) V DD (1) V A V SS (0) V DD (1) V DD (1) V DD (1) V SS (0) V DD (1) V DD (1) V DD (1) V SS (0) V B V SS Area: A NAND = 4 Transistors William Sandqvist william@kth.se

NOR-gate V DD V A V B V OH V A V SS (0) V SS (0) V DD (1) V OH V SS (0) V DD (1) V SS (0) V DD (1) V SS (0) V SS (0) V DD (1) V DD (1) V SS (0) V B V SS Area: A NOR = 4 Transistors William Sandqvist william@kth.se

Negativ logic ? • We can also turn the concepts and let L (low voltage) represent a logic 1 and let H (high voltage) represent a logic 0. – This is called negative logic. • An AND-function then becomes an OR-function and vice versa. – Negative logic or positive logic is really unimportant, but traditionally one uses positive logic. William Sandqvist william@kth.se

Three-state ? A CMOS-gate in addition to "1" or "0" is also provided with a third output state - the three-state ”Z”. ( = unconnected output). If many outputs are connected to the same line ("bus"), you can use one of the out-puts at a time . The other outputs are held in the Three-state condition. William Sandqvist william@kth.se

Three state ’Z’ Y = Y = ' Z ' A William Sandqvist william@kth.se

Transmissiongate Pass gate E A E Q A Q E Without going into the circuit details a Pass gate is composed of a PMOS transistor in parallel with an NMOS transistor. The gate is controlled by E (and E'). The pass gate could be compared to "regular" mechanical switch. A signal can go from A to Q, but also backwards from Q to A. Pass gates uses fewer transitors than ordinary gates, but have less drive capability. Area: A TG = 2 Transistors William Sandqvist william@kth.se

( Transmission gate pass gate ) E E A Q A Q E E V V E V OH A L L Z L H L H L Z H H H William Sandqvist william@kth.se

What is a multiplexor, MUX ? A multiplexor is a dataselector. Q=XS+YS X 1 X Q Q Y Y 0 S S William Sandqvist william@kth.se

Simplified drawing Example: MUX X Q Y X 1 S Q Q=XS+YS Y 0 X Q Y S S Of the inverter only the ring is left. Wires between the gates are presupposed. William Sandqvist william@kth.se

MUX with pass gates 2 MOS X 2 MOS Sel 2 MOS Y Q Area: A mux = 6 Transistors William Sandqvist william@kth.se

XOR with pass gates A 2 MOS B 2 MOS 2 MOS 2 MOS F = A ⊕ B Hardly obvious? Area: A XOR = 8 Transistors William Sandqvist william@kth.se

( XOR with pass gate ) A B F 0 0 0 = F B 0 1 1 1 0 1 = F B 1 1 0 William Sandqvist william@kth.se

William Sandqvist william@kth.se

Delays in circuits All wires in electronic circuits has capacitance. It takes a while for the voltage to reach the final value. These delays in circuits and between circuits restricts the speed. William Sandqvist william@kth.se

Typical delays NAND, NOR, NOT T NAND = standard T NOT ½ T, 1 T (if NAND-gate) NAND-NAND 2T (2 NAND in serial) AND-OR 4T, 3T (NAND-NOT+NOR-NOT) XOR, XNOR, MUX 3…5T XOR, MUX (with TG) 2T William Sandqvist william@kth.se

Optimized structures for MUX DeMorgan AND-OR NAND-NAND Area: A MUX = 2+6+6+6=20 Area: A MUX = 6 Transistors Transistors Delay: T MUX = ~2T NAND Delay: T MUX = 5T NAND Area: A MUX =2+4+4 = Best! = 10 Transistors Delay: T MUX = 3T NAND William Sandqvist william@kth.se

Optimized structures for XOR DeMorgan Area: A XOR =2+2+4+4=12 Area: A XOR =2+2+6+6+6=22 Transistors Transistors Delay: T XOR =3T NAND Delay: T XOR =5T NAND Nand only Area: A XOR =8 Transistorer Area: A XOR =4+4+4+4=16 Delay: T XOR =~2T NAND Transistors Delay: T XOR =3T NAND Best! William Sandqvist william@kth.se

Fan-out and Fan-in • Fan-out - one output drives many inputs. The output is loaded down by the sum of the inputs capacitances => delay T is load-dependent. • Fan-in - a gate has many inputs. This means that it has more internal capacitance => the internal delay time T i (also called the intrinsic delay) becomes larger. William Sandqvist william@kth.se

Gates with multiple inputs V DD One rarely use gates with more than four V Q inputs. V A A long line of series- T i V B connected transistors give slow action! V C V SS 3-input NAND William Sandqvist william@kth.se

High Fan-in is solved with tree structures ⋅ ⋅ = ⋅ ⋅ a b c a ( b c ) DeMorgan ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ + ⋅ = ⋅ ⋅ ⋅ a b c d ( a b ) ( c d ) ( a b ) ( c d ) a b c d For the price of increased gate-depth (delay) William Sandqvist william@kth.se

Moore tree structures For the price of increased gate- + + + = + + + a b c d ( a b ) ( c d ) depth (delay), but the effect of internal capacitances had ⊕ ⊕ ⊕ = ⊕ ⊕ ⊕ a b c d ( a b ) ( c d ) been worse. Can you prove these equivalents? ⊕ ⊕ ⊕ = ⊕ ⊕ ⊕ ( ) ( ) a b c d a b c d William Sandqvist william@kth.se

Fan-out • The number of Gate-inputs as a gate drives is referred to as fan-out • All gate inputs that are driven increases the capacitive load N 1 V f f To inputs of To inputs of x x n other inverters n other inverters C n = n ⋅ C (a) Inverter that drives n other inverters (b) Equivalent circuit for timing purposes William Sandqvist william@kth.se

Fan-out • Delays from different fan-outs V for n = 1 f V DD V for n = 4 f Gnd 0 Time William Sandqvist william@kth.se

Buffer • A buffer is a circuit that implements the function f ( x ) = x ( out = in ) • The idea of the buffer is to increase the drive capability of capacitive loads - To increase the driving ability one uses larger transistors - Buffers can be sized so that they can drive larger currents William Sandqvist william@kth.se

High Fan-out – use buffer x En f 3W En W 0 0 Z x f 0 1 0 1 0 Z 1 1 1 En x f Non-inverting Buffer Tri-state Buffer High-Fan-Out Buffer William Sandqvist william@kth.se

Critical path = + + f x x x x x x x 2 0 2 1 2 0 1 x 0 x 1 x 2 f Which way to the output takes the longest time? x 0 x 1 x 2 ? William Sandqvist william@kth.se

”Critical path” = + + f x x x x x x x 2 0 2 1 2 0 1 x 0 x 1 x 2 f x 0 x 1 x 2 all pass NOT , AND, and OR, On their way to the output f , but x 2 has the load of three inputs, x 0 and x 1 only two . ”Critical path” becomes x 2 ! William Sandqvist william@kth.se

William Sandqvist william@kth.se

Look-up-tables (LUT) A LUT with n inputs can realize all combinational Programmable 0/1 1 functions with n inputs cells The usual size in an 0/1 0 FPGA is n =4 1 f 0 0/1 1 0/1 0 x 2 x 1 Two-input LUT William Sandqvist william@kth.se

Ex. XOR-function Programmed 0 1 values Multiplexer 1 0 x x f 1 1 2 f 0 0 0 0 1 1 0 1 1 0 0 1 0 1 x 2 x 1 1 1 0 Two-input LUT William Sandqvist william@kth.se

William Sandqvist william@kth.se

7400-series standard chips William Sandqvist william@kth.se