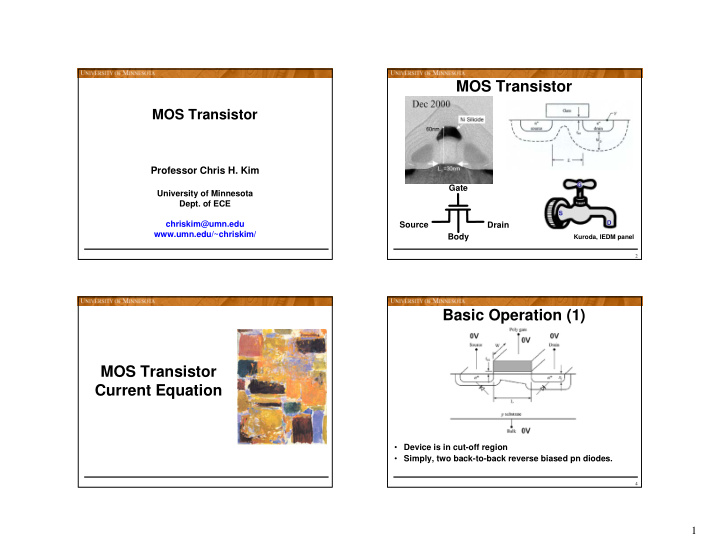
MOS Transistor MOS Transistor Professor Chris H. Kim Gate - PowerPoint PPT Presentation

MOS Transistor MOS Transistor Professor Chris H. Kim Gate University of Minnesota Dept. of ECE chriskim@umn.edu Source Drain www.umn.edu/~chriskim/ Body Kuroda, IEDM panel 2 Basic Operation (1) MOS Transistor Current Equation • Device is in cut-off region • Simply, two back-to-back reverse biased pn diodes. 4 1

Basic Operation (2) Basic Operation (3) • With a positive gate bias, electrons are pulled toward the positive gate electrode • Current flows from drain to source with a positive drain • Given a large enough bias, the electrons start to “invert” voltage the surface (p � n type), a conductive channel forms • What is current in terms of V gs , V ds , V bs ? • Threshold voltage V t 5 6 Channel Length Modulation MOS Current I ds = 0 V gs < V t : cut-off • Pinch-off depletion layer width increases as the drain I ds = μ e C ox W/L ((V gs -V t ) V ds -0.5V ds2 ) voltage increases 0 < V ds < V gs - V t : triode (linear) mode • Extreme case of this is punch-through I ds = μ e C ox W/(2L) (V gs -V t ) 2 L = − ζ = × = × + λ o L L V I I I ( 1 V ) − ζ o ds ds dsat dsat ds 0 < V gs - V t < V ds : saturation mode L V o ds 7 8 2

Simulation versus Model (NMOS) Simulation versus Model (PMOS) • Not as bad as the NMOS device • The square-law model doesn’t match well with simulations • Still large discrepancies at high E-field conditions • Only fits for low V gs , low V ds (low E-field) conditions 9 10 Velocity Saturation Simulation versus Model (I ds vs. V gs ) • E-fields have gone up as dimensions scale • Unfortunately, carrier velocity in silicon is limited • Saturation current does not increase quadratically • Electron velocity saturates at a lower E-field than holes • Mobility ( μ e =v/E) degrades at higher E-fields • The simulated curves looks like a straight line • Main reason for discrepancy: velocity saturation • Simple piecewise linear model can be used 11 12 3

Velocity Saturation Velocity Saturation • Plug it into the original current equation μ E 2 v = < ⎧ = ⎛ ⎞ e 2 v for E E sat E W V 1 ⎜ ⎟ μ − − × < c 1 ⎪ ds c μ C ( V V ) V ( V V ) ⎜ ⎟ ⎛ ⎞ n n ⎛ ⎞ ⎪ e ox gs t ds ds dsat V ⎝ ⎠ L 2 ⎜ ⎟ + + E e ⎜ ⎟ ∴ = ds ⎨ 1 1 ⎜ ⎟ I ⎝ ⎠ E ds E L ⎝ ⎠ ⎪ c c ⎪ − − > ⎩ C Wv ( V V V ) ( V V ) = > [Toh, Ko, Meyer, v for E E ox sat gs t dsat ds dsat JSSC, 8/1988] sat c Equate the two expressions to get − ( ) V V E L = • Modeled through a variable mobility gs t c V − + dsat ( V V ) E L • n=1 for PMOS, n=2 for NMOS gs t c • To get an analytical expression, let’s assume n=1 13 14 Simulation versus Model Unified MOS Model unified model simulation 700 1.2V 600 500 1.0V linear I DS [V] 400 vel. saturation 0.8V 300 200 0.6V saturation 100 0.4V 0 V dsat • Model incorporating velocity saturation matches fairly 0 0.2 0.4 0.6 0.8 1 1.2 well with simulation V DS [V] 15 16 4

Alpha Power Law Unified MOS Model Equations • Simple empirical model for short channel MOS W [Sakurai and Newton, α = μ − I C ( V V ) JSSC 1990] ds e ox gs t 2 L • Parameter α is between 1 and 2 • α =1-1.2 for short channel γ - body effect parameter devices • Parameters α and V t are fitted • Model presented is compact and suitable for hand analysis. to measured data for minimum square error � fitted V t can be • Still have to keep in mind the main approximation: that different from physical V t V DSat is constant. • But the model still works fairly well. 17 18 5