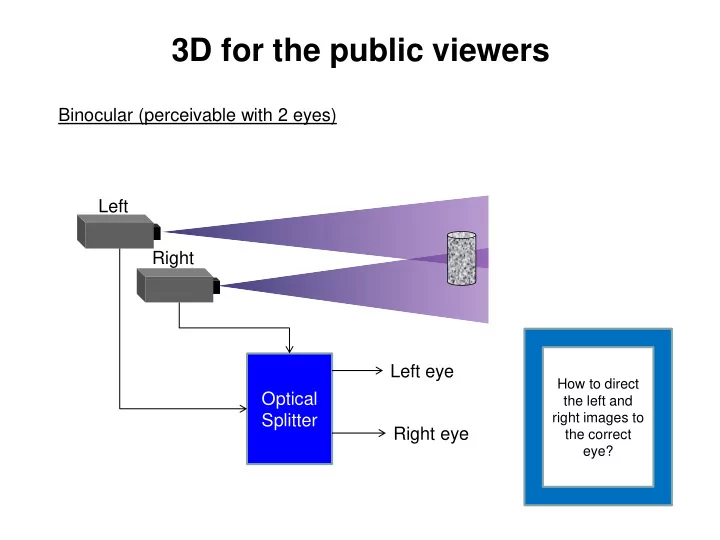

3D for the public viewers Binocular (perceivable with 2 eyes) Left Right Left eye How to direct Optical the left and right images to Splitter Right eye the correct eye?
Anaglyph Blue filter Red filter Transmission 475nm 650nm 475nm Wavelength Right picture Red component only Left picture Blue component only Projection Red filter Blue filter
Polarized glasses based Stereoscopic 3D Usual approach: Display left and right eyes images on the same screen, and utilizes polarized glasses to direct each image to the corresponding eye. Malus’s law: Intensity is attenuated by the square of the cosine of the angle between the polarization directions of the light and the polarizing filter, as I = cos 2 Hence, the viewing level must be strictly horizontal to avoid ghosting. I . o Right picture polarized at 90 degree Left picture polarized at 0 degree Projection 90 degree polarizer 0 degree polarizer
Circular Polarizing filter Circular Polarizing filter: polarization rotates clockwise or anticlockwise after passing through it. Anticlockwise polarizer 90 o 0 o Polarizing angle Unpolarized light 90 o 0 o Unpolarized light Clockwise polarizer http://upload.wikimedia.org/wikipedia/commons/d/d1/Circular.Polarization.Circularly.Polarized.Light_Left.H and.Animation.305x190.255Colors.gif
Circular Polarizing filter Circular Polarizing filter: polarization rotates clockwise or anticlockwise after passing through it. Anticlockwise polarizer 90 o 0 o Unpolarized light 90 o Block 0 o Anticlockwise polarized light Clockwise polarizer
Circular Polarized glasses based Stereoscopic 3D Using circular polarized images and glasses avoid the constraint on level viewing. Adopted in modern 3D movies and TV signals. Right picture Anticlockwise polarized Left picture Clockwise polarized Projection Anticlockwise polarizer Clockwise polarizer
Stereoscopic 3D on TV Time division multiplexing Left and right images are shown in the odd and even ( or even and odd) frames, respectively. Active shutter glass L R L R L R Synchronized to respective field Left image Right image Lower brightness as glasses are only conducted at 50% of time. Expensive and bulky active shutter glasses.
Stereoscopic 3D on TV Film-type Patterned Retarder: LG Checker sampling technology Left eye picture (cw-cp) Right eye picture (acw-cp) A film with circular polarizing element is placed on each pixel. Left and right pixels have different direction of polarization (cw- cp and acw-cp). No flickering, brighter image. Low cost glasses. Anticlockwise Clockwise circular polarizer circular polarizer Picture resolution is lowered by a factor of 2.
Glass free (naked eye) 3D viewing Origin: Classic lenticular 3D photographs. Basic concept: Interleave 2 or more views on the screen. Overlay a lenticular lens array, or a parallax barrier. The lens array or barrier deflects each view to its respective direction. Interlaced image Lenticular lens array Left image pixel Right image pixel Left Eye Right Eye Interleaving and viewing of a pair of stereoscopic images
Glass free (naked eye) 3D viewing Interleaving left and right images on the screen can be described as a decimation and interpolation process. 1. Each image is decimated into a new image that is half of its original width. 2. The decimated images are interpolated and interleave on the screen. A Interpolation A Blank strip filled by the second image Decimation Decimation leads to distortion which cannot be fully recovered with interpolation. Decimation, interpolation, and Interleaving of a pair of stereoscopic images
Decimation x ( n ) y ( n ) M M is the decimation factor x’ ( n ) x ( n ) e.g. M = 2 -4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4 y ( n ) Something is lost!
Decimation in 2 steps: 1 st step x’ ( n ) x ( n ) x ( n ) n = 0 , + M , +2 M , + 3M , +4 M , ... x’ ( n ) = 0 otherwise = = − x n '( ) i n x n ( ) ( ) ( n rM ) x n ( ) (1) =− r
Decimation: 1 st step = = − x n '( ) i n x n ( ) ( ) ( n rM ) x n ( ) (1) =− r i ( n ) 0 -2M -M M 2M i ( n ) is a periodic impulse train that can be expressed as − 2 M 1 1 j M nk = − = (2) i n ( ) ( n rM ) e M =− = r k 0
Decimation: 1 st step = = − x n '( ) i n x n ( ) ( ) ( n rM ) x n ( ) (1) =− r − 2 M 1 1 j M nk = − = i n ( ) ( n rM ) e (2) M =− = r k 0 − − 2 2 M 1 M 1 x n ( ) 1 j M nk j M nk = = (3) x n '( ) e x n e ( ) M M = = k 0 k 0
Decimation: 2 nd step x’ ( n ) x ( n ) y ( n ) y ( n ) = x ’( Mn ) (4) According to equation (3) − − 2 2 M 1 M 1 x n ( ) 1 j M nk j M nk = = x n '( ) e x n e ( ) M M = = k 0 k 0 − M 1 1 = = (5) x nM e j 2 nk y n ( ) x Mn '( ) ( ) M = k 0
Decimation: 2 nd step is 𝑌 𝑓 𝑘𝜕 . The frequency spectrum of x 𝑜 Converting the decimated signal y 𝑜 to frequency space with discrete Fourier transform: − 2 k − M 1 1 j = j M Y e ( ) X e M = k 0 1. The frequency spectrum is scaled by a factor M . Frequency axis is lengthened. 2. There are M copies (replicas) of the original base-band (scale in width). 3. The replicas are located at 2𝜌𝑙 𝑁 | 0≤𝑙<𝑁 . 4. If the bandwidth of the signal exceeds 2𝜌 𝑁 , the replicas overlap with each other, leading to aliasing error.
Decimation: illustration x’ ( n ) x ( n ) y ( n ) X e j ( ) − /4 /4 /2 /4 /4 /2 /4 /4 /2 /4 0 e j X '( ) M= 4 − /4 /4 /2 /4 /4 /2 /4 /4 /2 /4 0 Y e j ( ) − /4 /4 /2 /4 /4 /2 /4 /4 /2 /4 0
Interpolation x ( n ) y ( n ) M e.g. M = 2 x ( n ) y ( n ) -4 -3 -2 -1 0 1 2 3 4 -2 -1 0 1 2
Interpolation x ( n ) y ( n ) M x ( n/M ) n = 0 , +M , +2M , +3M , ... y ( n ) = (6) 0 otherwise 𝑍 𝑓 𝑘𝜕 = 𝑌 𝑓 𝑘𝜕𝑁 The frequency spectrum is scaled by a factor M . The frequency scale is compressed.
Interpolation X e j ( ) − /4 /4 /2 /4 /4 /2 /4 /4 /2 /4 0 j Y e ( ) ( ) = j M X e M= 4 − /4 /4 /2 /4 /4 /2 /4 /4 /2 /4 0 No change other than a scaling of the frequency axis.
Glass free (naked eye) 3D viewing Does it works on monitor? A pixel on the screen Intuitively, we can simply interleave the pixels on the monitor in alternating left and right manner.
Glass free (naked eye) 3D viewing Early product by Sharp: Stereoscopic (2 views) with rainbow moiré pattern Left pixel Right pixel Usual pixel arrangement Interleaving and viewing multi-view images Slight difference in viewing positions capture incomplete pixel components
Glass free (naked eye) 3D viewing Avoiding rainbow moiré patterns: Rotate screen by 90 degree. Left pixel Right pixel Rotated pixel arrangement Interlaced images Lenticular lens array Slight difference in viewing positions capture same pixel components. Very Left Eye Right Eye poor resolution for large number of Interleaving and viewing multi-view images views.
Glass free (naked eye) 3D viewing with Auto-stereoscopic monitor 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 1 2 3 4 5 6 7 Lenticular lens array Magnified view of one lens column Very poor horizontal resolution
Glass free (naked eye) 3D viewing with Auto-stereoscopic monitor Rotating the lenticular lens array by certain degree
Glass free 3D viewing Slant Lenticular technology Philips patent: US6,064,424 (May 2000) Distribute resolution degradation to horizontal and vertical directions View 4 View 2 View 3 2 6 2 6 2 6 2 4 6 2 4 6 2 4 6 2 4 6 2 4 6 2 4 6 4 4 4 1 5 1 3 5 1 3 1 5 1 3 5 1 3 5 1 3 5 1 3 5 1 3 5 3 5 3 6 4 6 4 6 2 2 4 6 2 4 6 2 4 6 2 2 4 6 2 4 6 2 4 6 2 2 4 2 2 5 3 5 3 5 1 3 5 1 3 5 1 3 5 1 3 5 1 3 5 1 3 5 1 3 1 1 4 2 4 2 4 6 2 4 6 2 4 6 2 4 6 2 4 6 2 4 6 2 4 6 2 6 6
Packaging and distribution of muti-view signals An early attempt to compress 3D stereoscopic sequences has been made by the MPEG with the incorporation of the Multiview Profile (MVP) [1][2] into the existing MPEG II standard. The approach is largely an extension of the temporal scalability, but so far the MVP has not been adopted as a commercially available service. [1] M. Tanimoto and T. Fuji, “Utilization of inter-view correlation for multiple view video coding”, ISO/IEC JTC1/SC29/WG11 M11014, July 2004. “Using [2] H. Wang, et al, inter-view prediction for multi-view video compression”, ISO/IEC JTC1/SC29/WG11 M10512, Mar. 2004.
Recommend
More recommend