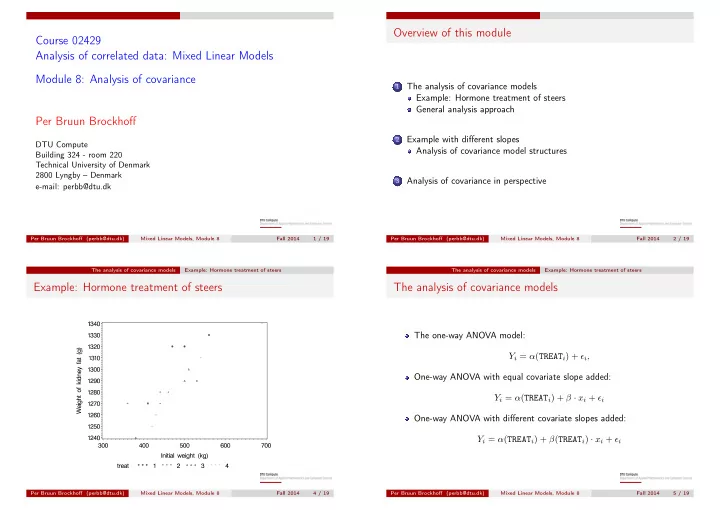

Overview of this module Course 02429 Analysis of correlated data: Mixed Linear Models Module 8: Analysis of covariance The analysis of covariance models 1 Example: Hormone treatment of steers General analysis approach Per Bruun Brockhoff Example with different slopes 2 DTU Compute Analysis of covariance model structures Building 324 - room 220 Technical University of Denmark 2800 Lyngby – Denmark Analysis of covariance in perspective 3 e-mail: perbb@dtu.dk Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 1 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 2 / 19 The analysis of covariance models Example: Hormone treatment of steers The analysis of covariance models Example: Hormone treatment of steers Example: Hormone treatment of steers The analysis of covariance models The one-way ANOVA model: Y i = α ( TREAT i ) + ǫ i , One-way ANOVA with equal covariate slope added: Y i = α ( TREAT i ) + β · x i + ǫ i One-way ANOVA with different covariate slopes added: Y i = α ( TREAT i ) + β ( TREAT i ) · x i + ǫ i Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 4 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 5 / 19
The analysis of covariance models General analysis approach The analysis of covariance models General analysis approach General analysis approach Example: Hormone treatment of steers. Randomized Block experiment: Hormone treatment 1 2 3 4 1 Test equal slopes model versus different slopes model (Interaction) Weight Y Weight Y Weight Y Weight Y 2 If significant interaction: Block 1 560 1330 440 1280 530 1290 690 1340 Block 2 470 1320 440 1270 510 1300 420 1250 YES, there is a significant treatment effect! Block 3 410 1270 360 1270 380 1240 430 1260 Summarize information within the different slopes setting. Block 4 500 1320 460 1280 500 1290 540 1310 3 If NOT significant interaction: Different slopes model: Test the treatment effect in the equal slopes model. Y i = d ( BLOCK i ) + α ( HORMONE i ) + β ( HORMONE i ) · WEIGHT i + ǫ i (Remove the covariate again if not significant) Summarize information within the equal slopes setting. Equal slopes model: Y i = d ( BLOCK i ) + α ( HORMONE i ) + β · WEIGHT i + ǫ i Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 6 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 7 / 19 The analysis of covariance models General analysis approach The analysis of covariance models General analysis approach Steers example: Results An analysis ignoring the covariate. Source of Numerator Denominator F P-value variation degrees degrees Randomized Block model: of freedom of freedom weight 1 3.69 (28.09) (0.0076) Y i = d ( BLOCK i ) + α ( HORMONE i ) + ǫ i treat 3 6.5 (1.59) (0.2821) weight*treat 3 6.61 1.44 0.3147 Results: Source of Numerator degrees Denominator degrees F P variation of freedom of freedom treat 3 9 2.04 0.1786 Source of Numerator degrees Denominator degrees F P The treatment difference is NOT detected! variation of freedom of freedom weight 1 11 67.5 < 0.0001 treat 3 11 6.38 0.0092 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 8 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 9 / 19
The analysis of covariance models General analysis approach The analysis of covariance models General analysis approach Summary and post hoc analysis. Summary and post hoc analysis, cont. The final equal slopes model: Y i = d ( BLOCK i ) + α ( HORMONE i ) + β · WEIGHT i + ǫ i Better with LSMEANS: where α ( HORMONE i ) + ˆ ˆ β · WEIGHT d ( BLOCK i ) ∼ N (0 , σ 2 B ) , ǫ i ∼ N (0 , σ 2 ) Parameter LSMEAN LOWER UPPER σ 2 = 126 . 1 σ 2 Hormone 1 α (1) + β · 477 . 5 1308 1295 1320 ˆ B = 0 , ˆ Hormone 2 α (2) + β · 477 . 5 1292 1279 1305 Parameter Estimate Hormone 3 α (3) + β · 477 . 5 1279 1267 1292 Hormone 1 α (1) 1150.6 Hormone 4 α (4) + β · 477 . 5 1276 1263 1289 Hormone 2 α (2) 1135.3 Hormone 3 α (3) 1122.2 Hormone 4 α (4) 1119.1 Slope β 0.3287 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 10 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 11 / 19 Example with different slopes Example with different slopes Example with different slopes Summary and post hoc analysis σ 2 = 1 . 20 σ 2 ˆ B = 18 . 25 , ˆ 3 4 1 4 40 The regression parameters: 2 3 Parameter Estimate 3 35 Treat 1 α (1) 26.8 y 2 3 1 4 2 1 4 Treat 2 α (2) 21.9 4 3 2 1 1 Treat 3 α (3) 28.6 30 2 4 1 Treat 4 α (4) 22.4 3 2 Slope 1 β (1) 0.219 10 15 20 25 30 35 40 x Slope 2 β (2) 0.496 Slope 3 β (3) 0.263 Source of Numerator degrees Denominator degrees F P-value Slope 4 β (4) 0.443 variation of freedom of freedom X*treat 3 9.34 5.12 0.0233 Tell the story for different values of the covariate: ˆ α ( k ) + ˆ E Y i = ˆ β ( k ) · x 0 Choose Small, medium and large x 0 value! Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 13 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 14 / 19
Example with different slopes Analysis of covariance model structures Example with different slopes Analysis of covariance model structures Analysis of covariance model structures Summary and post hoc analysis, cont. 7 3 ● 4 1 4 6 ● ● 5 40 ● y ● + β x 4 Treat 1 α 1 2 ● 3 + β x ● 3 α Treat 2 2 ● 3 + β x 2 α Treat 3 3 ● x LOW x HIGH x 35 2 3 1 y 2 4 6 8 10 4 2 x Equal slopes model 1 4 4 3 2 1 1 5 ● 30 + β x α 1 4 1 2 4 1 ● 3 3 ● α 2 + β 2 x 2 ● y ● ● 2 10 15 20 25 30 35 40 ● x ● α + β 1 3 x 3 ● x LOW x x HIGH 0 2 4 6 8 10 x Different slopes model Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 15 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 16 / 19 Analysis of covariance in perspective Analysis of covariance in perspective Analysis of covariance in perspective Overview of this module Covariate measurements The analysis of covariance models 1 can occur in any type of experiment (Split-plot etc.) Example: Hormone treatment of steers can be on different levels (observational unit and/or other factors) General analysis approach can occur on several variables The general approach: Example with different slopes Add the covariate term to the model including interactions. 2 1 Simplify the interactions with the covariate as much as possible Analysis of covariance model structures 2 Do the testing, summary and post hoc analysis in the resulting model. 3 If more than one: find the best(s)! 4 Analysis of covariance in perspective 3 Baseline measurements: ANCOVA better than analyzing differences! Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 18 / 19 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 8 Fall 2014 19 / 19
Recommend
More recommend