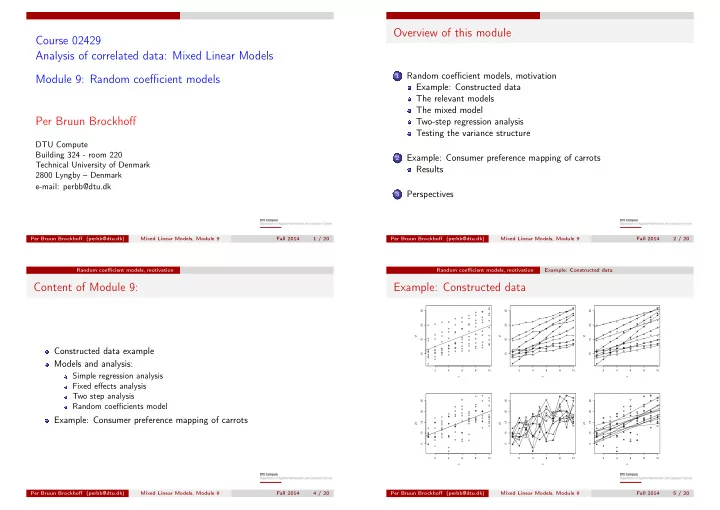
Overview of this module Course 02429 Analysis of correlated data: - PowerPoint PPT Presentation

Overview of this module Course 02429 Analysis of correlated data: Mixed Linear Models Random coefficient models, motivation 1 Module 9: Random coefficient models Example: Constructed data The relevant models The mixed model Per Bruun Brockhoff Two-step regression analysis Testing the variance structure DTU Compute Building 324 - room 220 Example: Consumer preference mapping of carrots 2 Technical University of Denmark Results 2800 Lyngby – Denmark e-mail: perbb@dtu.dk Perspectives 3 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 1 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 2 / 20 Random coefficient models, motivation Random coefficient models, motivation Example: Constructed data Content of Module 9: Example: Constructed data 25 25 25 20 20 20 y1 y1 y1 15 15 15 Constructed data example 10 10 10 Models and analysis: 2 4 6 8 10 2 4 6 8 10 2 4 6 8 10 Simple regression analysis x x x Fixed effects analysis Two step analysis 25 25 25 Random coefficients model 20 20 20 Example: Consumer preference mapping of carrots 15 15 15 y2 y2 y2 10 10 10 5 5 5 2 4 6 8 10 2 4 6 8 10 2 4 6 8 10 x x x Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 4 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 5 / 20

Random coefficient models, motivation The relevant models Random coefficient models, motivation The mixed model Models A mixed model The simple regression model: Splitting the mean and variance structure: y j = α + βx j + ǫ j y i = α + βx i + a ( subject i ) + b ( subject i ) x i + ǫ i Different FIXED regression lines: a ( k ) ∼ N (0 , σ 2 a ) , b ( k ) ∼ N (0 , σ 2 b ) , ǫ i ∼ N (0 , σ 2 ) y i = α ( subject i ) + β ( subject i ) x i + ǫ i Or slightly more general: Different RANDOM regression lines: � σ 2 � σ ab a ) , ǫ i ∼ N (0 , σ 2 ) ( a ( k ) , b ( k )) ∼ N (0 , y i = a ( subject i ) + b ( subject i ) x i + ǫ i σ 2 σ ab b where Allowing for correlation between between intercepts and slopes. a ( k ) ∼ N ( α, σ 2 a ) , b ( k ) ∼ N ( β, σ 2 b ) , ǫ i ∼ N (0 , σ 2 ) Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 6 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 7 / 20 Random coefficient models, motivation Two-step regression analysis Random coefficient models, motivation Two-step regression analysis Two-step regression analysis – constructed data Constructed data, cont. For “nice“ data sets (like the constructed data): Observed variances for slopes (two-step): Random coefficient regression corresponds to two-step analysis: Carry out a regression analysis for each subject. Data set 1: s 2 1 β = 0 . 2465 ˆ Do subsequent calculations on the parameter estimates from these 2 regression analyzes to obtain the average slope (and intercept) and Data set 2: s 2 β = 0 . 2130 their standard errors. ˆ Results: Estimated variance components (Random coefficient model): Data set 1 Data set 2 σ 2 = 0 . 0732 α β α β σ 2 Data set 1: ˆ b = 0 . 2456 , ˆ Average 10.7279 0.9046 7.8356 1.2152 SE 1.2759 0.1570 0.9255 0.1460 and for data set 2: Lower 7.8416 0.5495 5.7419 0.8850 Upper 13.6142 1.2597 9.9293 1.5454 σ 2 = 17 . 07 σ 2 Data set 2: ˆ b = 0 . 021 , ˆ NB: These are the (fixed effects) results from the random coefficient model. Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 8 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 9 / 20

Random coefficient models, motivation Two-step regression analysis Random coefficient models, motivation Testing the variance structure Example: Constructed data Notes Random coefficent models tells the proper story about the data 25 25 25 Two-step procedure only strictly valid in certain nice cases 20 20 20 y1 y1 y1 It is possible to test the equal slopes hypothesis: 15 15 15 10 10 10 H 0 : σ 2 b = 0 2 4 6 8 10 2 4 6 8 10 2 4 6 8 10 By the REML likelihood test: x x x G = − 2 l REML, 1 − ( − 2 l REML, 2 ) 25 25 25 20 20 20 Data set 2, NON-significant: 15 15 15 y2 y2 y2 G = − 2 l REML, 1 − ( − 2 l REML, 2 ) = 0 . 65 10 10 10 5 5 5 Data set 1, EXTREMELY significant: 2 4 6 8 10 2 4 6 8 10 2 4 6 8 10 x x x G = − 2 l REML, 1 − ( − 2 l REML, 2 ) = 249 . 9 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 10 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 11 / 20 Example: Consumer preference mapping of carrots Example: Consumer preference mapping of carrots Results Example: Consumer preference mapping of carrots Significance testing approach Factors: 103 consumers in 2 groups (Homesize) 12 1 Simplify the variance part of the model prod 11 12 carrot products 1236 1 [I] 1122 0 1 (G statistics) 103 2 Y-data: Preference scores [cons] 102 size 1 2 Then simplify the fixed/systematic structure X-data: Sensory measurements on the products. (Table of F-tests of fixed effects) Aim: Study average relationships between preference and 2 sensory Results, final model: score variables . Starting model, FIXED part: = α ( size i ) + β 2 · sens2 i + a ( cons i ) y i Homesize, average intercepts and slopes depending on homesize. + b 2 ( cons i ) · sens2 i + d ( prod i ) + ǫ i Starting model, RANDOM part: Random regression coefficients on the two sensory variables. where a ( k ) ∼ N (0 , σ 2 a ) , b 2 ( k ) ∼ N (0 , σ 2 b 2 ) , k = 1 , . . . 103 . Random product effect and d ( prod i ) ∼ N (0 , σ 2 P ) , ǫ i ∼ N (0 , σ 2 ) Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 13 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 14 / 20

Example: Consumer preference mapping of carrots Results Example: Consumer preference mapping of carrots Results Results Results The variance part: No significant variation in sens1 coefficients. Confidence intervals: Significant variation in sens2 coefficients. 2.5 % 97.5 % Significant (additional) product variation. No significant correlation between sens2 intercepts and slopes. .sig01 0.03 0.08 .sig02 0.36 0.53 Estimates - all parameters: .sig03 0.09 0.29 ˆ 0.0545 σ b 2 .sigma 0.98 1.07 σ a ˆ 0.442 Homesize1 4.74 5.08 ˆ 0.1774 σ P Homesize3-Homesize1 -0.45 -0.03 ˆ σ 1.0194 sens2 0.04 0.10 α ( Homesize1 ) ˆ 4.91 α ( Homesize3 ) ˆ 4.67 ˆ 0.071 β 2 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 15 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 16 / 20 Example: Consumer preference mapping of carrots Results Perspectives Results, fixed part Random coefficient models in perspective No relation of preference to sens1. Significant relation to sens2 (sweetness): Random extensions of regression and/or ANCOVA models. ˆ β 2 = 0 . 071 , [0 . 04 , 0 . 10] Relevant for hierarchical/clustered data. Also relevant for repeated measures data. The homesize story: Can be directly extended to polynomial structures. α (1) + ˆ ˆ β 2 · sens2 = 4 . 91 , [4 . 73 , 5 . 09] Can extend with residual correlation structures. α (2) + ˆ ˆ = 4 . 67 , [4 . 47 , 4 . 85] β 2 · sens2 May enter as components of any kind of analysis. α (1) − ˆ ˆ α (2) = 0 . 25 , [0 . 04 , 0 . 46] Homes with more persons tend to have a slightly lower preference in general for such carrot products. Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 17 / 20 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 19 / 20

Perspectives Overview of this module Random coefficient models, motivation 1 Example: Constructed data The relevant models The mixed model Two-step regression analysis Testing the variance structure Example: Consumer preference mapping of carrots 2 Results Perspectives 3 Per Bruun Brockhoff (perbb@dtu.dk) Mixed Linear Models, Module 9 Fall 2014 20 / 20