Lecture 4: Problem solving as search: Solution = a finite sequence - PowerPoint PPT Presentation


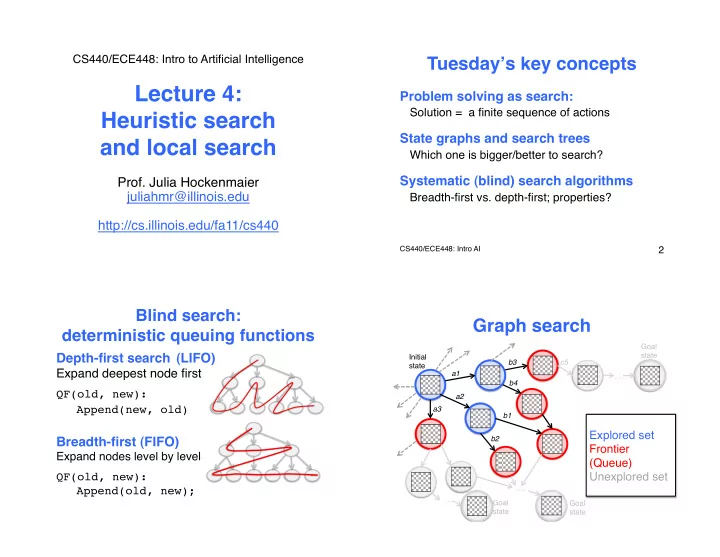
 CS440/ECE448: Intro to Artificial Intelligence � Tuesday ʼ s key concepts � Lecture 4: 
 Problem solving as search: � Solution = a finite sequence of actions 
 Heuristic search 
 � State graphs and search trees � and local search � Which one is bigger/better to search? 
 � Systematic (blind) search algorithms � Prof. Julia Hockenmaier � juliahmr@illinois.edu � Breadth-first vs. depth-first; properties? 
 � � http://cs.illinois.edu/fa11/cs440 � � � � CS440/ECE448: Intro AI � 2 � � Blind search: 
 Graph search � deterministic queuing functions � Goal � Depth-first search � (LIFO) �� state � Initial � A b3 � c5 � state � ! Expand deepest node first � a1 � …. "! ! ! ! B C D b4 � ! "! "! "! QF(old, new): 
 "! a2 � ! � Append(new, old) 
 E F G H I � J a3 � "! b1 � ! � A "! Explored set � ! Breadth-first (FIFO) � b2 � "! ! Frontier B C D Expand nodes level by level � "! (Queue) � ! "! QF(old, new): 
 Unexplored set � E F G H I � J ! ! "! …. � Append(old, new); � "! …. � Goal � Goal � ! ! state � state � "! "!


 
 
 Today ʼ s key questions � How can we find the optimal solution? � We need to assign values to solutions 
 Informed 
 How can we find a better solution if we (heuristic) search � can only foresee the effect (=value) of the next action? � This is local search. � � CS440/ECE448: Intro AI � 5 � Considering the cost of solutions � Heuristic search: priority queue � We may not just want to find any solution, 
 Heuristic search algorithms sort the nodes but the cheapest solution, if: � on the queue according to a cost function : 
 � – Each action has a (positive, finite) cost � QF(a,b): 
 – Some solutions may be cheaper than others 
 � sort (append(a,b), CostFunction) 
 � � The cost function is an estimate of the true cost. � Nodes with the lowest estimated cost have 
 � the highest priority. � CS440/ECE448: Intro AI � 7 � 8 �

Heuristic graph search � Cost from root to node: g(n) � SEARCH(Problem P, Queuing Function QF): 
 local: n, q, e; 
 g*(n): Minimum cost from root to n � q ! new List(Initial_State(P)); 
 Loop: 
 g*(n) is the sum of the costs for each action 
 � if q == () return failure; 
 from the root to node n. � � n ! Pop(q); 
 This requires a cost function for actions � � if n solves P return n; 
 add n.STATE to e 
 g(n): Computable approximation to g*(n) 
 for m in Expand(n): 
 if m is not in e or q: 
 For trees: g(n) == g*(n) � q ! QF(q,{m}); � /*NEW: we want to find the cheapest goal!*/ 
 � else if m.STATE in q with higher cost : 
 � � � q ! replace(q, m.STATE, m); 
 end � 9 � CS440/ECE448: Intro AI � 10 � Uniform-cost search � Uniform-cost search illustrated � 1 3 99 � S � F � Sort the queue by path cost g(n): � g = 0 � g = 99 � 211 � First expand the node with lowest g(n) � 80 � 2 R � � 5 g=80 � 4 QF(a,b): sort(Append(a,b), g) � P � 101 � B � 97 � g = 177 � g = 278 � S:0 � [R:80, F:99] � R:80 � [F:99, P:177] � F:99 � [P:177, B:310] � P:177 � [B:278, B:310] � B:278 [B:310] � CS440/ECE448: Intro AI � 11 � CS440/ECE448: Intro AI � 12 �


 Properties of 
 How close are we to the goal? � uniform-cost search � Initial state � I � Complete if b is finite, and each action has positive (non-zero) cost 
 } (gets stuck in loops of zero-cost actions) 
 g*(n) � Optimal. � � n � Node n � Time and space complexity similar to } ??? � breadth-first search if costs are uniform � (possibly much worse otherwise) � G � Goal state � CS440/ECE448: Intro AI � 13 � 14 � Cost from node to goal: h(n) � Greedy best-first search � h*(n): the minimum cost from n to any goal 
 Sort the queue by heuristic function h(n): � h*(n) is generally unknown � First expand the node with lowest h(n) � � h(n): computable approximation to h* 
 QF(a,b): sort(Append(a,b), h ) � h(n) is called the heuristic function � n � � � } h*(n) � Problem: This ignores g(n) � G CS440/ECE448: Intro AI � 15 � CS440/ECE448: Intro AI � 16 �

Properties of 
 Total cost: f*(n) � greedy best-first search � Initial state � I � Similar to DFS: � Tree-search version is incomplete. � } f*(n) = g*(n) + h*(n) � Graph-search version is complete 
 g*(n) � in finite state spaces. Both are not optimal. � f*(n) is the lowest cost � solution from the n � Node n � Worst-case time and space complexity initial state to a goal } h*(n) � similar to DFS 
 constrained through n � (actual complexity depends on h) � G � Goal state � CS440/ECE448: Intro AI � 17 � 18 � Total estimated cost: f(n) � A* search � Initial state � I � Sort the queue by total estimated cost f(n): � f(n) = g(n) + h(n) � First expand the node with lowest f(n) � } f(n) approximates � g(n) � the lowest cost QF(a,b): sort(Append(a,b), f ) � solution from the � n � Node n � initial state to a � } h(n) � goal constrained through n � G � Goal state � 19 � CS440/ECE448: Intro AI � 20 �


 Properties of A* search � Tree-search A* is optimal if… � A* is complete if b is finite, and each action …h(n) is an admissible heuristic � has positive (non-zero) cost 
 Admissible heuristics never overestimate 
 � the future cost. 
 Its complexity depends on the heuristic � function h(n) � Definition � h(n) is admissible: ! n " nodes: h(n) # h*(n) Is A* optimal? � CS440/ECE448: Intro AI � 21 � 22 � � Tree-search A* is optimal 
 Graph-search A* is optimal if… � if h(n) is admissible � Confused? � Confused? � This is optional This is In tree-search: g(n) = g*(n) � optional …h(n) is monotonic (=consistent) � material � material � If n is a goal : f(n) = f*(n) � Monotonic heuristics obey the triangle inequality : � The goal that is returned is the cheapest on the queue! � Going from n to the goal via n ʼ is at least as If n is not a goal : f(n) ≤ f*(n) � expensive as going from n to the goal. � g(n) + h(n) ≤ g*(n) + h*(n) � � n � cost(n, a, n ʼ ) � f*(n): true cost of cheapest goal that can be reached from n. 
 ! n ! n’ " nodes, n ʼ � h(n) � � ! a " actions with a(n) $ n’ If g no is a non-optimal goal, and n opt is an ancestor h(n ʼ ) � h(n) # cost(n, a, n’) + h(n’) 
 G � of the optimal goal g opt : f(n opt ) ≤ f(g opt ) < f(g no ) � � � n opt will be explored first! � NB.: every monotonic heuristic is also admissible � � � 23 � 24 � �

Possible Heuristic Functions � Graph-search A* is optimal if… � …h(n) is monotonic (=consistent) � Often simplify by relaxing some constraint � h(n) # cost(n, a, n’) + h(n’) � Confused? � This is optional � � h 1 : 3 � material � Proof sketch: � � h 2 (8-puzzle): 
 1. If h is monotonic, the values of f(n) along any count # tiles out of place � path are non-decreasing. (true by definition) � � h 3 (route-finding): 
 2. When n is expanded, g(n) = g*(n) � sum Manhattan metric distances � [we have found the cheapest path to n. ] � � Thus, sorting by f finds the cheapest goal first � Uniform-cost: h uniform-cost = 0 � 25 � 26 � Informed heuristics � Given: � A 1 * with heuristic function h 1 
 and � A 2 * with heuristic function h 2 � � � Both A 1 * and A 2 * are admissible � Local search � � A 1 * is more informed than A 2 * iff 
 for all non-goal nodes n h 1 (n) > h 2 (n) � � “More informed”: “guaranteed not to search more” � � 27 �

Motivation for local search � Local search algorithms: � How can we find the goal when: 
 Consider only the current node 
 � and the next action � - we can ʼ t keep a queue? 
 � (because we don ʼ t have the memory) 
 Also useful for optimization: � � - we don ʼ t want to keep a queue? 
 finding the best state according to 
 (because we just need to find the goal state, ) � an objective function � � - we can ʼ t enumerate the next actions? 
 (because there ʼ s an infinite number) 
 � � � CS440/ECE448: Intro AI � 30 � 8-queens � 8-queens by local search � Initial state: � A board with 8 queens, one in each column. � (we use a complete-state formulation ). � � Action: Move one queen to another square in its column. � � Heuristic function (score): 
 How many queens attack each other? � � CS440/ECE448: Intro AI � 31 � CS440/ECE448: Intro AI � 32 �

The state space landscape: 
 Possible successor states � minimizing cost… � cost � If queen in 14 14 18 12 14 13 13 12 The best first column 14 16 13 15 12 14 12 16 next moves here, current states � score = 15 � state � 14 12 18 13 15 12 14 14 15 14 14 13 16 13 16 14 17 15 14 16 16 goal state � 17 16 18 15 15 18 14 15 15 14 16 14 14 13 17 12 14 12 18 state space � CS440/ECE448: Intro AI � 33 � CS440/ECE448: Intro AI � 34 � …or maximizing 
 The state space landscape � an objective function � objective � objective � global goal state � function � function � maximum � = − cost � current current plateau � state � state � local maximum � state space � state space � CS440/ECE448: Intro AI � 35 � CS440/ECE448: Intro AI � 36 �