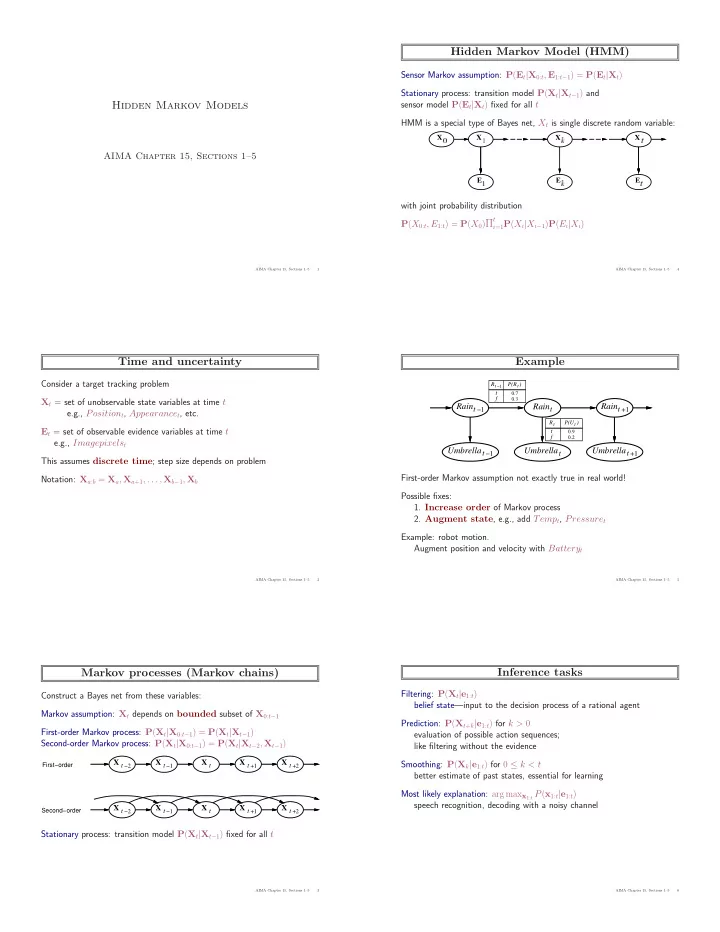
hidden markov model hmm
play

Hidden Markov Model (HMM) Sensor Markov assumption: P ( E t | X 0: t - PDF document

Oct 15, 2023 •287 likes •324 views

Hidden Markov Model (HMM) Sensor Markov assumption: P ( E t | X 0: t , E 1: t 1 ) = P ( E t | X t ) Stationary process: transition model P ( X t | X t 1 ) and Hidden Markov Models sensor model P ( E t | X t ) fixed for all t HMM is a

  1. Hidden Markov Model (HMM) Sensor Markov assumption: P ( E t | X 0: t , E 1: t − 1 ) = P ( E t | X t ) Stationary process: transition model P ( X t | X t − 1 ) and Hidden Markov Models sensor model P ( E t | X t ) fixed for all t HMM is a special type of Bayes net, X t is single discrete random variable: AIMA Chapter 15, Sections 1–5 with joint probability distribution P ( X 0: t , E 1: t ) = P ( X 0 ) Π t i =1 P ( X i | X i − 1 ) P ( E i | X i ) AIMA Chapter 15, Sections 1–5 1 AIMA Chapter 15, Sections 1–5 4 Time and uncertainty Example Consider a target tracking problem R t −1 P(R ) t t 0.7 f 0.3 X t = set of unobservable state variables at time t Rain t −1 Rain Rain t +1 t e.g., Position t , Appearance t , etc. R P(U ) t t E t = set of observable evidence variables at time t t 0.9 f 0.2 e.g., Imagepixels t Umbrella t −1 Umbrella Umbrella t +1 t This assumes discrete time ; step size depends on problem First-order Markov assumption not exactly true in real world! Notation: X a : b = X a , X a +1 , . . . , X b − 1 , X b Possible fixes: 1. Increase order of Markov process 2. Augment state , e.g., add Temp t , Pressure t Example: robot motion. Augment position and velocity with Battery t AIMA Chapter 15, Sections 1–5 2 AIMA Chapter 15, Sections 1–5 5 Markov processes (Markov chains) Inference tasks Filtering: P ( X t | e 1: t ) Construct a Bayes net from these variables: belief state—input to the decision process of a rational agent Markov assumption: X t depends on bounded subset of X 0: t − 1 Prediction: P ( X t + k | e 1: t ) for k > 0 First-order Markov process: P ( X t | X 0: t − 1 ) = P ( X t | X t − 1 ) evaluation of possible action sequences; Second-order Markov process: P ( X t | X 0: t − 1 ) = P ( X t | X t − 2 , X t − 1 ) like filtering without the evidence X t −2 X t −1 X t X t +1 X t +2 Smoothing: P ( X k | e 1: t ) for 0 ≤ k < t First−order better estimate of past states, essential for learning Most likely explanation: arg max x 1: t P ( x 1: t | e 1: t ) speech recognition, decoding with a noisy channel X t −2 X t −1 X t X t +1 X t +2 Second−order Stationary process: transition model P ( X t | X t − 1 ) fixed for all t AIMA Chapter 15, Sections 1–5 3 AIMA Chapter 15, Sections 1–5 6

  2. Filtering Filtering Aim: devise a recursive state estimation algorithm: Aim: devise a recursive state estimation algorithm: P ( X t +1 | e 1: t +1 ) = f ( e t +1 , P ( X t | e 1: t )) P ( X t +1 | e 1: t +1 ) = f ( e t +1 , P ( X t | e 1: t )) P ( X t +1 | e 1: t +1 ) = P ( X t +1 | e 1: t , e t +1 ) = α P ( e t +1 | X t +1 , e 1: t ) P ( X t +1 | e 1: t ) = α P ( e t +1 | X t +1 ) P ( X t +1 | e 1: t ) I.e., prediction + estimation. Prediction by summing out X t : P ( X t +1 | e 1: t +1 ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 , x t | e 1: t ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 | x t , e 1: t ) P ( x t | e 1: t ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 | x t ) P ( x t | e 1: t ) f 1: t +1 = Forward ( f 1: t , e t +1 ) where f 1: t = P ( X t | e 1: t ) Time and space constant (independent of t ) AIMA Chapter 15, Sections 1–5 7 AIMA Chapter 15, Sections 1–5 10 Filtering Filtering example Aim: devise a recursive state estimation algorithm: 0.500 0.627 0.500 0.373 P ( X t +1 | e 1: t +1 ) = f ( e t +1 , P ( X t | e 1: t )) True 0.500 0.818 0.883 False 0.500 0.182 0.117 Rain 0 Rain 1 Rain 2 P ( X t +1 | e 1: t +1 ) = P ( X t +1 | e 1: t , e t +1 ) = α P ( e t +1 | X t +1 , e 1: t ) P ( X t +1 | e 1: t ) = α P ( e t +1 | X t +1 ) P ( X t +1 | e 1: t ) Umbrella 1 Umbrella 2 P ( X t +1 | e 1: t +1 ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 | x t ) P ( x t | e 1: t ) P ( R t ) P ( U t ) R t − 1 R t t 0.7 t 0.9 f 0.3 f 0.2 AIMA Chapter 15, Sections 1–5 8 AIMA Chapter 15, Sections 1–5 11 Filtering Smoothing X 0 X 1 X k X t Aim: devise a recursive state estimation algorithm: P ( X t +1 | e 1: t +1 ) = f ( e t +1 , P ( X t | e 1: t )) E E k E t 1 Divide evidence e 1: t into e 1: k , e k +1: t : P ( X t +1 | e 1: t +1 ) = P ( X t +1 | e 1: t , e t +1 ) P ( X k | e 1: t ) = P ( X k | e 1: k , e k +1: t ) = α P ( e t +1 | X t +1 , e 1: t ) P ( X t +1 | e 1: t ) = α P ( X k | e 1: k ) P ( e k +1: t | X k , e 1: k ) = α P ( e t +1 | X t +1 ) P ( X t +1 | e 1: t ) = α P ( X k | e 1: k ) P ( e k +1: t | X k ) I.e., prediction + estimation. Prediction by summing out X t : = α f 1: k b k +1: t P ( X t +1 | e 1: t +1 ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 , x t | e 1: t ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 | x t , e 1: t ) P ( x t | e 1: t ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 | x t ) P ( x t | e 1: t ) AIMA Chapter 15, Sections 1–5 9 AIMA Chapter 15, Sections 1–5 12

  3. Smoothing Most likely explanation X 0 X 1 X k X t Most likely sequence � = sequence of most likely states!!!! Most likely path to each x t +1 E E k E t 1 = most likely path to some x t plus one more step Divide evidence e 1: t into e 1: k , e k +1: t : x 1 ... x t P ( x 1 , . . . , x t , X t +1 | e 1: t +1 ) max P ( X k | e 1: t ) = P ( X k | e 1: k , e k +1: t )   = P ( e t +1 | X t +1 ) max  P ( X t +1 | x t ) max x 1 ... x t − 1 P ( x 1 , . . . , x t − 1 , x t | e 1: t )  x t = α P ( X k | e 1: k ) P ( e k +1: t | X k , e 1: k ) Identical to filtering, except f 1: t replaced by = α P ( X k | e 1: k ) P ( e k +1: t | X k ) = α f 1: k b k +1: t m 1: t = x 1 ... x t − 1 P ( x 1 , . . . , x t − 1 , X t | e 1: t ) , max Backward message computed by a backwards recursion: I.e., m 1: t ( i ) gives the probability of the most likely path to state i . P ( e k +1: t | X k ) = Σ x k +1 P ( e k +1: t | X k , x k +1 ) P ( x k +1 | X k ) Update has sum replaced by max, giving the Viterbi algorithm: = Σ x k +1 P ( e k +1: t | x k +1 ) P ( x k +1 | X k ) m 1: t +1 = P ( e t +1 | X t +1 ) max x t ( P ( X t +1 | x t ) m 1: t ) = Σ x k +1 P ( e k +1 | x k +1 ) P ( e k +2: t | x k +1 ) P ( x k +1 | X k ) AIMA Chapter 15, Sections 1–5 13 AIMA Chapter 15, Sections 1–5 16 Smoothing example Viterbi example 0.500 0.627 0.500 0.373 Rain 1 Rain 2 Rain 3 Rain 4 Rain 5 True 0.500 0.818 0.883 forward False 0.500 0.182 0.117 true true true true true state space 0.883 0.883 smoothed paths 0.117 0.117 false false false false false true true false true true 0.690 1.000 umbrella backward 0.410 1.000 .8182 .5155 .0361 .0334 .0210 Rain 0 Rain 1 Rain 2 most likely paths .1818 .0491 .1237 .0173 .0024 m 1:1 m 1:2 m 1:3 m 1:4 m 1:5 Umbrella 1 Umbrella 2 Forward–backward algorithm: cache forward messages along the way Time linear in t (polytree inference), space O ( t | f | ) AIMA Chapter 15, Sections 1–5 14 AIMA Chapter 15, Sections 1–5 17 Most likely explanation Example Umbrella Problems Filtering: P ( X t +1 | e 1: t +1 ) = α P ( e t +1 | X t +1 ) Σ x t P ( X t +1 | x t ) P ( x t | e 1: t ) =: f 1: t +1 Smoothing: P ( X k | e 1: t ) = α f 1: k b k +1: t P ( e k +1: t | X k ) = Σ x k +1 P ( e k +1 | x k +1 ) P ( e k +2: t | x k +1 ) P ( x k +1 | X k ) =: b k +1: t R t − 1 P ( R t ) R t P ( U t ) t 0.7 t 0.9 f 0.3 f 0.2 P ( R 3 |¬ u 1 , u 2 , ¬ u 3 ) = ? arg max R 1:3 P ( R 1:3 |¬ u 1 , u 2 , ¬ u 3 ) = ? P ( R 2 |¬ u 1 , u 2 , ¬ u 3 ) = ? AIMA Chapter 15, Sections 1–5 15 AIMA Chapter 15, Sections 1–5 18

Download Presentation
Download Policy: The content available on the website is offered to you 'AS IS' for your personal information and use only. It cannot be commercialized, licensed, or distributed on other websites without prior consent from the author. To download a presentation, simply click this link. If you encounter any difficulties during the download process, it's possible that the publisher has removed the file from their server.

Recommend

Hidden Markov Models Pratik Lahiri Introduction A hidden Markov model (HMM) is a

Hidden Markov Models Pratik Lahiri Introduction A hidden Markov model (HMM) is a

Hidden Markov Models Pratik Lahiri Introduction A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved (hidden) states. We call the observed event

741 views • 13 slides
Multivariate Hidden Markov model An application to study correlations among cryptocurrency

Multivariate Hidden Markov model An application to study correlations among cryptocurrency

Introduction Proposed Hidden Markov Model (HMM) Data Results Conclusions References Multivariate Hidden Markov model An application to study correlations among cryptocurrency log-returns Fulvia Pennoni Bartolucci F. , Forte G.

440 views • 28 slides
A C Standard model has 1-1 correspondence between symbols and states, P(A | T) thus P ( x i

A C Standard model has 1-1 correspondence between symbols and states, P(A | T) thus P ( x i

Outline Markov chains CSCE 471/871 Lecture 3: Markov Chains and Hidden Markov Models Hidden Markov models (HMMs) Formal definition Finding most probable state path (Viterbi algorithm) Stephen D. Scott Forward and backward

640 views • 5 slides
The Hidden Markov The Hidden Markov Model (HMM) Model (HMM) 1 Lecture Outline Lecture Outline

The Hidden Markov The Hidden Markov Model (HMM) Model (HMM) 1 Lecture Outline Lecture Outline

Digital Speech Processing Digital Speech Processing Lecture 20 Lecture 20 The Hidden Markov The Hidden Markov Model (HMM) Model (HMM) 1 Lecture Outline Lecture Outline Theory of Markov Models discrete Markov processes

991 views • 87 slides
Hidden Markov Models Markov Model (Finite State Machine with Probs) Modeling a sequence of

Hidden Markov Models Markov Model (Finite State Machine with Probs) Modeling a sequence of

Hidden Markov Models Markov Model (Finite State Machine with Probs) Modeling a sequence of weather observations Hidden Markov Models Assume the states in the machine are not observed and we can observe some output at certain states. Hidden

692 views • 26 slides
Hidden Markov Models Training Selecting model parameters What we know The terminology and

Hidden Markov Models Training Selecting model parameters What we know The terminology and

Hidden Markov Models Training Selecting model parameters What we know The terminology and notation of hidden Markov models ( HMMs ) The forward- and backward-algorithms for determining the likelihood p ( X ) of a sequence of

1.02k views • 60 slides
Lecture 9: Hidden Markov Model Kai-Wei Chang CS @ University of Virginia kw@kwchang.net Couse

Lecture 9: Hidden Markov Model Kai-Wei Chang CS @ University of Virginia kw@kwchang.net Couse

Lecture 9: Hidden Markov Model Kai-Wei Chang CS @ University of Virginia kw@kwchang.net Couse webpage: http://kwchang.net/teaching/NLP16 CS6501 Natural Language Processing 1 This lecture v Hidden Markov Model v Different views of HMM v HMM

579 views • 34 slides
Markov Models Kunsch, H.R., State Space and Hidden Markov Models . ETH- Zurich, Zurich;

Markov Models Kunsch, H.R., State Space and Hidden Markov Models . ETH- Zurich, Zurich;

State Space and Hidden Markov Models Kunsch, H.R., State Space and Hidden Markov Models . ETH- Zurich, Zurich; Aliaksandr Hubin Oslo 2014 Contents 1. Introduction 2. Markov Chains 3. Hidden Markov and State Space Model 4. Filtering and

853 views • 37 slides
1 X 1 X 2 X 3 Ghostbusters HMM Chain Rule and HMMs E 1 E 2 E 3 P(X 1 ) = uniform 1/9 1/9

1 X 1 X 2 X 3 Ghostbusters HMM Chain Rule and HMMs E 1 E 2 E 3 P(X 1 ) = uniform 1/9 1/9

Hidden Markov Models 1 Hidden Markov Models Markov chains not so useful for most agents Need observations to update your beliefs Hidden Markov models (HMMs) Underlying Markov chain over states X You observe outputs (effects) at

617 views • 7 slides
Hidden Markov Models (HMM) Many slides from Michael Collins and HMMs Overview I The Tagging

Hidden Markov Models (HMM) Many slides from Michael Collins and HMMs Overview I The Tagging

Hidden Markov Models (HMM) Many slides from Michael Collins and HMMs Overview I The Tagging Problem I Generative models, and the noisy-channel model, for supervised learning I Hidden Markov Model (HMM) taggers I Basic definitions I Parameter

968 views • 37 slides
Hidden Markov Model, Kalman Filter and A Unifying View Mu Li April 16, 2013 Outline Hidden

Hidden Markov Model, Kalman Filter and A Unifying View Mu Li April 16, 2013 Outline Hidden

Recitations for 10-701: Hidden Markov Model, Kalman Filter and A Unifying View Mu Li April 16, 2013 Outline Hidden Markov Model Kalman Filter A Unifying View of Linear Gaussian Models based on slides from Simma &amp; Batzoglou Outline

770 views • 37 slides
Markov chains and Hidden Markov Models 9000 Markov chains and HMMs We will discuss: Markov

Markov chains and Hidden Markov Models 9000 Markov chains and HMMs We will discuss: Markov

Markov chains and Hidden Markov Models 9000 Markov chains and HMMs We will discuss: Markov chains Hidden Markov Models (HMMs) Algorithms: Viterbi, forward, backward, posterior decoding Profile HMMs Baum-Welch algorithm 9001

1.16k views • 87 slides
Tagging Problems, and Hidden Markov Models Michael Collins, Columbia University Overview The

Tagging Problems, and Hidden Markov Models Michael Collins, Columbia University Overview The

Tagging Problems, and Hidden Markov Models Michael Collins, Columbia University Overview The Tagging Problem Generative models, and the noisy-channel model, for supervised learning Hidden Markov Model (HMM) taggers Basic

778 views • 38 slides
1 Real HMM Examples Real HMM Examples Speech recognition HMMs: Machine translation HMMs:

1 Real HMM Examples Real HMM Examples Speech recognition HMMs: Machine translation HMMs:

Hidden Markov Models CSE 473: Artificial Intelligence Markov chains not so useful for most agents Hidden Markov Models Eventually you dont know anything anymore Need observations to update your beliefs Hidden Markov models

567 views • 9 slides
CSE P 590 A Markov Models and Hidden Markov Models

CSE P 590 A Markov Models and Hidden Markov Models

CSE P 590 A Markov Models and Hidden Markov Models http://upload.wikimedia.org/wikipedia/commons/b/ba/Calico_cat Dosage Compensation Reminder: Proteins Read DNA and X-Inactivation E.g.: 2 copies (mom/dad) of each

1.28k views • 21 slides
1 Real HMM Examples Real HMM Examples Speech recognition HMMs: Machine translation HMMs:

1 Real HMM Examples Real HMM Examples Speech recognition HMMs: Machine translation HMMs:

Hidden Markov Models CSE 473: Artificial Intelligence Hidden Markov Models Markov chains not so useful for most agents Eventually you dont know anything anymore Need observations to update your beliefs Hidden Markov models (HMMs)

253 views • 7 slides
Prob obab abil ilit ity y an and d Tim Time: H Hid idde den Ma Marko kov v Mo Mode

Prob obab abil ilit ity y an and d Tim Time: H Hid idde den Ma Marko kov v Mo Mode

Prob obab abil ilit ity y an and d Tim Time: H Hid idde den Ma Marko kov v Mo Mode dels ls (H (HMM MMs) s) Com omputer Science c cpsc sc322, Lecture 3 32 (Te Text xtboo ook k Chpt 6.5.2) June, 2 20, 2 2017 CPSC

405 views • 24 slides
Poverty and Inequality Dynamics. Ira N. Gang, Rutgers University Ksenia Gatskova, IOS-Regensburg

Poverty and Inequality Dynamics. Ira N. Gang, Rutgers University Ksenia Gatskova, IOS-Regensburg

Poverty and Inequality Dynamics. Ira N. Gang, Rutgers University Ksenia Gatskova, IOS-Regensburg John Landon-Lane, Rutgers University Myeong-Su Yun, Tulane University Paper prepared for the UNU-WIDER Conference: Inequality Measurement,

753 views • 29 slides
Randomized Algorithms Lecture 3: Occupancy, Moments and deviations, Randomized selection

Randomized Algorithms Lecture 3: Occupancy, Moments and deviations, Randomized selection

Randomized Algorithms Lecture 3: Occupancy, Moments and deviations, Randomized selection Sotiris Nikoletseas Associate Professor CEID - ETY Course 2013 - 2014 Sotiris Nikoletseas, Associate Professor Randomized Algorithms - Lecture 3

603 views • 34 slides
Ground state expansion and the spectral gap of local Hamiltonians Elizabeth Crosson California

Ground state expansion and the spectral gap of local Hamiltonians Elizabeth Crosson California

ICTP Workshop on Adiabatic Quantum Computers, 2016 Ground state expansion and the spectral gap of local Hamiltonians Elizabeth Crosson California Institute of Technology H 2( H E 0 ) 2 ( S ) 2 ( S ) Isoperimetric

351 views • 17 slides
The simplex method is strongly polynomial for deterministic Markov decision processes Ian Post

The simplex method is strongly polynomial for deterministic Markov decision processes Ian Post

The simplex method is strongly polynomial for deterministic Markov decision processes Ian Post Yinyu Ye Fields Institute November 29, 2013 Post, Ye Simplex on MDPs Fields, Nov 29, 2013 1 / 18 Markov Decision Processes A Markov decision

496 views • 32 slides
Markov Chains and Hidden Markov Models COMP 571 - Spring 2015 Luay Nakhleh, Rice University

Markov Chains and Hidden Markov Models COMP 571 - Spring 2015 Luay Nakhleh, Rice University

Markov Chains and Hidden Markov Models COMP 571 - Spring 2015 Luay Nakhleh, Rice University Markov Chains and Hidden Markov Models Modeling the statistical properties of biological sequences and distinguishing regions based on these models

873 views • 58 slides
18.175: Lecture 32 More Markov chains Scott Sheffield MIT 1 18.175 Lecture 32 Outline General

18.175: Lecture 32 More Markov chains Scott Sheffield MIT 1 18.175 Lecture 32 Outline General

18.175: Lecture 32 More Markov chains Scott Sheffield MIT 1 18.175 Lecture 32 Outline General setup and basic properties Recurrence and transience 2 18.175 Lecture 32 Outline General setup and basic properties Recurrence and transience 3 18.175

479 views • 14 slides
Markov Chains Toolbox Search: uninformed/heuristic Adversarial search Probability

Markov Chains Toolbox Search: uninformed/heuristic Adversarial search Probability

Markov Chains Toolbox Search: uninformed/heuristic Adversarial search Probability Bayes nets Naive Bayes classifiers Reasoning over time In a Bayes net, each random variable (node) takes on one specific value. Good for

408 views • 37 slides

More recommend