Cell implementation HMM (HMM hidden Markov model) Authors: Jakub - PowerPoint PPT Presentation

IBM ČVUT Student Research Project 2006 Cell – implementation HMM (HMM – hidden Markov model) Authors: Jakub Horák Jiří Hošna

HMM Project specification • Implement one of algorithm used for HMM on Cell architecture • In our case we choose Viterbi algorithm IBM ČVUT Student Research Project 2006 (2 z 16)

HMM Applications of hidden Markov models • speech recognition • optical character recognition • bioinformatics (DNA analysis) • machine translation • and many more... • generally is used for time lines analysis Why hidden Markov models Because is an algorithm which can be solved in polynomial • time. IBM ČVUT Student Research Project 2006 (3 z 16)

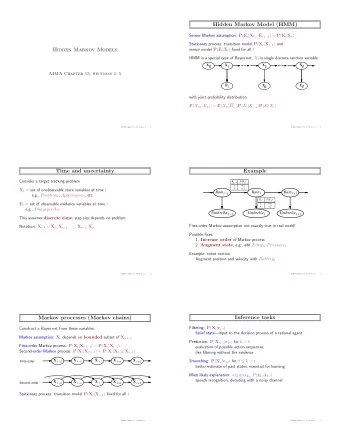
HMM Andrey Andreyevich Markov • 1856 – 1922 • Russian mathematician • Best known for his work on theory of stochastic processes. His research later became known • as Markov chains. • A Markov chain is a sequence of random variables where the value of next variable, depends only upon the value of past variable. IBM ČVUT Student Research Project 2006 (4 z 16)

HMM • Markov's models (including hidden) are special type of finite stochastic automaton. • Enable represent statistical dependencies of observation (states) over time. • A Markov model is a automaton which moves from state to state depending (only) on the previous n states. The model is called an order n model where n is the number of states affecting the choice of next state. IBM ČVUT Student Research Project 2006 (5 z 16)

HMM First order Markov model: • Is a simplest model which can be described as a automaton, where the choice of state is made only on the basis of the previous state. • Can be defined as a pair (K,A), where K ... finite set of states A ... transition matrix IBM ČVUT Student Research Project 2006 (6 z 16)

HMM Example: first order Markov model states: k 1 : snowy or rainy k 2 : cloudy k 3 : sunny transition probability matrix: A = ∣ 0.8 ∣ 0.4 0.3 0.3 0.2 0.6 0.2 0.1 0.1 IBM ČVUT Student Research Project 2006 (7 z 16)

HMM Hidden Markov Model • In a regular Markov model, the state is directly visible to the observer. • In a hidden Markov model, the state is not directly visible, but variables influenced by the state are visible. Each state has a probability distribution over the possible output tokens. Thus the sequence of tokens generated by an HMM gives some information about the sequence of states . IBM ČVUT Student Research Project 2006 (8 z 16)

HMM Hidden Markov Model • First state hidden Markov model can be defined as a triple (K, A, B), where K ... finite set of states A ... transition matrix B ... confusion matrix IBM ČVUT Student Research Project 2006 (9 z 16)

HMM Example: first order hidden Markov model IBM ČVUT Student Research Project 2006 (10 z 16)

HMM T here are 3 canonical problems to solve with HMMs • Given the model parameters, compute the probability of a particular output sequence. Solved by the forward algorithm. • Given the model parameters, find the most likely sequence of (hidden) states which could have generated a given output sequence. Solved by the Viterbi algorithm. • Given an output sequence, find the most likely set of state transition and output probabilities. Solved by the Baum- Welch algorithm or the Reversed Viterbi algorithm. IBM ČVUT Student Research Project 2006 (11 z 16)

HMM Viterbi Algorithm For i, i=1...n let  1 =   i ∗ b ik 1  For t, t=2...T and i, i=1...n let  t  i  = max   t − 1  j ∗ a ji ∗ b ik t  j  t  i  = argmax j   t − 1  j ∗ a ji  let i t = argmax i   T  i   For t, t=(T-1)...2 let i t =  t  1  i t  1  IBM ČVUT Student Research Project 2006 (12 z 16)

Implementation • Data types: double • Operations: array multiplivation, max value and index of max value of result array => seqentional algorithm (no SIMD ops) so we used RPC for CBE • Documentation says: ! (simple) realization IBM ČVUT Student Research Project 2006 (13 z 16)

IDL interface interface array_mul { import "../stub.h"; [async_b] idl_id_t do_array_mul ([in] int array_size, [in] int one, [in, size_is(array_size)] double delta_vec_prev[], [in, size_is(array_size)] double a_mat_col[], [in, size_is(one)] double e_prob[], [out, size_is(one)] double max[], [out, size_is(one)] int max_i[]); } IBM ČVUT Student Research Project 2006 (14 z 16)

Algorithm in C for (i = 0; i < N; ++i) { delta_vec[i] = init[i] * e_mat[i][obs[0]]; } for (i = 1; i < T; ++i) { for (j = 0; j < N; ++j) { delta_vec_prev[j] = delta_vec[j]; delta_vec[j] = 0; } for (j = 0; j < N; ++j) do_array_mul(N, 1, delta_vec_prev, a_mat[j], &e_mat[j][obs[i]], &delta_vec[j], &phi_mat[i][j]); } idl_join_all_do_array_mul(); } IBM ČVUT Student Research Project 2006 (15 z 16)

Implementation probles • Ferora virus on our PCs • A lot of documentation, but the most important things missig there • Simulator is too slow and some functions are unusable with screen resolution 1024x768 • And others ... IBM ČVUT Student Research Project 2006 (16 z 16)