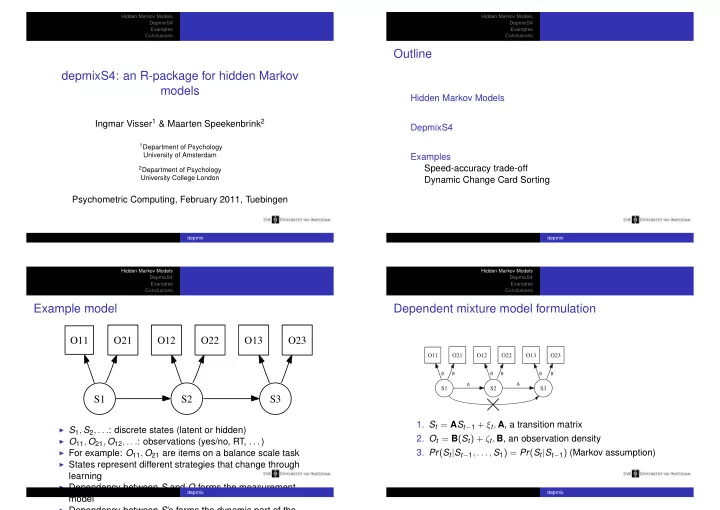

Hidden Markov Models Hidden Markov Models DepmixS4 DepmixS4 Examples Examples Conclusions Conclusions Outline depmixS4: an R-package for hidden Markov models Hidden Markov Models Ingmar Visser 1 & Maarten Speekenbrink 2 DepmixS4 1 Department of Psychology University of Amsterdam Examples Speed-accuracy trade-off 2 Department of Psychology University College London Dynamic Change Card Sorting Psychometric Computing, February 2011, Tuebingen depmix depmix Hidden Markov Models Hidden Markov Models DepmixS4 DepmixS4 Examples Examples Conclusions Conclusions Example model Dependent mixture model formulation O11 O21 O12 O22 O13 O23 O11 O21 O12 O22 O13 O23 B B B B B B A A S1 S2 S3 S1 S2 S3 1. S t = A S t − 1 + ξ t , A , a transition matrix ◮ S 1 , S 2 , . . . : discrete states (latent or hidden) 2. O t = B ( S t ) + ζ t , B , an observation density ◮ O 11 , O 21 , O 12 , . . . : observations (yes/no, RT, . . . ) ◮ For example: O 11 , O 21 are items on a balance scale task 3. Pr ( S t | S t − 1 , . . . , S 1 ) = Pr ( S t | S t − 1 ) (Markov assumption) ◮ States represent different strategies that change through learning ◮ Dependency between S and O forms the measurement depmix depmix model ◮ Dependency between S ’s forms the dynamic part of the
Hidden Markov Models Hidden Markov Models DepmixS4 DepmixS4 Examples Examples Conclusions Conclusions Likelihood Relationship to other models 1. Latent Markov model T 2. Dependent Mixture model � � Pr ( O 1 , . . . , O T ) = Pr ( O t | S t , A , B ) , 3. Bayesian network (with latent variables) q t = 1 4. State-space model (discrete) q an arbitrary hidden state sequence 5. Symbolic dynamic model 6. Regime switching models ◮ q : an enumeration of all possible state sequences ( n T ) 7. . . . ◮ Leave out the sum over q ( S t known): complete data likelihood O11 O21 O12 O22 O13 O23 ◮ Note: likelihood is not computed directly (impractical for large T ) S1 S2 S3 depmix depmix Hidden Markov Models Hidden Markov Models DepmixS4 DepmixS4 Examples Examples Conclusions Conclusions Why do we need them? DepmixS4 1. Piagetian development, ◮ R -package conservation, balance scale ◮ depmixS4 fits dep endent mix ture models 2. Concept identification learning [Jansen and Van der Maas, 2002] ◮ mixture components are generalized linear models (and 3. Strategy switching: Backwards learning curve others . . . ) Speed-accuracy trade-off 1.0 ◮ Markov dependency between components 0.8 4. Iowa Gambling task proportion errors 0.6 In short: depmixS4 fits hidden Markov models of generalized 5. Weather Prediction task 0.4 0.2 linear models in both large N, small T as well as N=1, T large 6. Climate change 0.0 samples. 5 10 15 20 [Visser and Speekenbrink, 2010] trials [Schmittmann et al., 2006] speed 7.0 depmix depmix 6.5 rt 6.0 5.5
Hidden Markov Models Hidden Markov Models DepmixS4 DepmixS4 Examples Examples Conclusions Conclusions Transition & initial model Response models Each row of the transition matrix and the initial state Current options for the response models are models from the probabilities: generalized linear modeling framework, and some additional distributions. ◮ is modeled as a multinomial distribution From glm : ◮ uses the logistic link function to include covariates ◮ normal distribution; continuous, gaussian data ◮ can have time-dependent covariates ◮ binomial (logit, probit); binary data Transition probability ◮ Poisson (log); count data 1.0 ◮ gamma distribution 0.8 Additional distributions: 0.6 probability ◮ multinomial (logistic or identity link); multiple choice data 0.4 ◮ multivariate normal 0.2 ◮ exgaus distribution (from the gamlss package); response 0.0 time data -1.0 -0.5 0.0 0.5 1.0 ◮ it is easy to add new response distributions covariate depmix depmix Hidden Markov Models Hidden Markov Models DepmixS4 DepmixS4 Speed-accuracy trade-off Examples Examples Dynamic Change Card Sorting Conclusions Conclusions Optimization Speed-accuracy: data speed 7.0 6.5 rt 6.0 5.5 5.0 0.8 depmixS4 uses: corr 0.4 0.0 ◮ EM algorithm (interface to glm functions in R) 0.8 0.6 Pacc 0.4 ◮ Direct optimization of the raw data log likelihood for fitting 0.2 0.0 contrained models (using Rsolnp ) 0 50 100 150 Time ◮ Three blocks with N=168,134,137 trials (first block shown) ◮ Speeded reaction time task ◮ Speed and accuracy manipulated by reward variable ◮ Question: is there a single (linear) relationship between responses and covariate or switching between regimes? More data in: [Dutilh et al., 2011] depmix depmix
Hidden Markov Models Hidden Markov Models DepmixS4 Speed-accuracy trade-off DepmixS4 Speed-accuracy trade-off Examples Dynamic Change Card Sorting Examples Dynamic Change Card Sorting Conclusions Conclusions Speed-accuracy: linear model predictions Speed-accuracy: two-state model Model predicted RTs 7.0 6.5 RT ◮ FG=fast guessing 6.0 ◮ SC=stimulus controlled 5.5 ◮ Response times also modeled 5.0 ◮ Pay-off for accuracy as covariate on the transition 0 50 100 150 trial probabilities depmix depmix Hidden Markov Models Hidden Markov Models DepmixS4 Speed-accuracy trade-off DepmixS4 Speed-accuracy trade-off Examples Dynamic Change Card Sorting Examples Dynamic Change Card Sorting Conclusions Conclusions Speed-accuracy: two-state model Speed-accuracy: switching model Model predicted RTs 7.0 6.5 RT Fitting this in depmixS4 : 6.0 mod1 <- depmix(list(rt~1,corr~1), 5.5 + data=speed, transition=~Pacc, nstates=2, + family=list(gaussian(), multinomial("identity")), 5.0 + ntimes=c(168,134,137)) 0 50 100 150 trial fm1 <- fit(mod1) depmix depmix
Hidden Markov Models Hidden Markov Models DepmixS4 Speed-accuracy trade-off DepmixS4 Speed-accuracy trade-off Examples Dynamic Change Card Sorting Examples Dynamic Change Card Sorting Conclusions Conclusions Speed-accuracy: transition probabilities What is DCCS? Transition probability functions 6.5 1.0 ◮ task 1: sort by color RT P ◮ task 2: sort by shape 6.0 0.5 P(switch from FG to SC) ◮ measures: ability to P(stay in SC) RTs on increasing Pacc RTs on decreasing Pacc switch/flexibility 5.5 0.0 0.0 0.5 1.0 Pacc ◮ transition probabilities as function of covariate ◮ hysteresis: asymmetry between switching from FG to SC and vice versa depmix depmix Hidden Markov Models Hidden Markov Models DepmixS4 Speed-accuracy trade-off DepmixS4 Speed-accuracy trade-off Examples Dynamic Change Card Sorting Examples Dynamic Change Card Sorting Conclusions Conclusions DCCS: data DCCS: research questions ◮ data consists of 6 trials ◮ can we characterize the (task 2) remaining group? ◮ traditional analyses: ◮ are there children in 1. 0/1 correct: transition, shifting from perseveration one strategy to 2. 5/6 correct: switching another? ◮ alternative: are they simply guessing? depmix depmix
Hidden Markov Models Hidden Markov Models DepmixS4 Speed-accuracy trade-off DepmixS4 Speed-accuracy trade-off Examples Dynamic Change Card Sorting Examples Dynamic Change Card Sorting Conclusions Conclusions DCCS: theory DCCS: results ◮ cusp model predicts ◮ P: perseveration state instability in the ◮ S: switch state transitional phase ◮ transition P->S much ◮ shifting back and forth larger than transition between ‘strategies’ S->P ◮ hysteresis: assymetry ◮ this model better than a in transition model without probabilities transitions depmix depmix Hidden Markov Models Hidden Markov Models DepmixS4 Speed-accuracy trade-off DepmixS4 Speed-accuracy trade-off Examples Dynamic Change Card Sorting Examples Dynamic Change Card Sorting Conclusions Conclusions DCCS: results Other applications ◮ 30 to 40 % of 3/4 year olds are in the ◮ Climate change data transitional phase, ◮ Learning on the Iowa Gambling Task shifting between strategies ◮ Balance scale task ◮ Categorization learning depmix depmix
Recommend
More recommend