Prob obab abil ilit ity y an and d Tim Time: H Hid idde - PowerPoint PPT Presentation

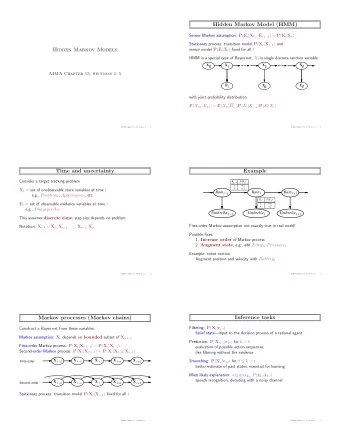
Prob obab abil ilit ity y an and d Tim Time: H Hid idde den Ma Marko kov v Mo Mode dels ls (H (HMM MMs) s) Com omputer Science c cpsc sc322, Lecture 3 32 (Te Text xtboo ook k Chpt 6.5.2) June, 2 20, 2 2017 CPSC 322, Lecture 32 Slide 1

Lectu ture re Ov Overv rvie iew • Recap p • Markov Models • Markov Chain • Hi Hidden Mar arko kov v Mod odels ls CPSC 322, Lecture 32 Slide 2

Answerin ing Querie ies unde der Un Uncertai ainty Probab abil ility ity Theory ry Dynamic mic Bayesia ian n Network rk Sta tati tic B Belief Netw twork & V Variab able le Elimi mina nation ion Hidden n Markov ov Models St Student t Tracing ng in Monitori oring ng tutorin ing g Sy Systems ms Robotics BioInforma rmati tics cs (e.g credit t cards) Markov ov Chains Natural al Language age Diagno nosti stic c Processin ssing Systems Sy ms (e.g., ., medici cine ne) Email il spam m filters rs CPSC 322, Lecture 32 Slide 3

Stat atio ionar ary Ma y Markov Ch v Chai ain ( (SMC MC) A st station onary Marko kov Chain : for all t >0 • P ( S t+1 | S 0 ,…, S t ) = and • P ( S t +1 | We only need to specify and • Simple Model, easy to specify • Often the natural model • The network can extend indefinitely • Var ariat ations of SM SMC ar are at at th the c core o of most t Nat atural al L Lan anguag age Processing (NLP) ap applicat ations! CPSC 322, Lecture 32 Slide 4

Lectu ture re Ov Overv rvie iew • Recap • Markov Models • Markov Chain • Hi Hidden Mar arko kov v Mod odels ls CPSC 322, Lecture 32 Slide 5

Ho How c can an we we mi minim imal ally ly extend Ma d Markov Ch v Chai ains? • Maintaining the Marko kov and st station onary assumptions? A useful situation to model is the one in which: • the reasoning system doe oes s not ot have access ss to the states • but can make ke obse servations s that give some information about the current state CPSC 322, Lecture 32 Slide 6

Hidden Markov Model • A Hidden M Mar arkov Mo v Model (HMM) starts with a Markov chain, and adds a noisy observation about the state at each time step: • |domain(S)| = k • |domain(O)| = h • P ( S 0 ) specifies initial conditions • P ( S t+1 | S t ) specifies the dynamics A. 2 2 x h B. h h x h • P ( O t | S t ) specifies the sensor model C . . k k x h CPSC 322, Lecture 32 Slide 7 D. D. k k x k

Hidden Markov Model • A Hidden Mar arkov v Model ( (HMM) starts with a Markov chain, and adds a noisy observation about the state at each time step: • |domain(S)| = k • |domain(O)| = h • P ( S 0 ) specifies initial conditions • P ( S t+1 | S t ) specifies the dynamics • P ( O t | S t ) specifies the sensor model CPSC 322, Lecture 32 Slide 8

Exa xamp mple le: Localization for “Pushed around” Robot • Loc ocaliza zation on (where am I?) is a fundamental problem in rob obot otics • Suppose a robot is in a circular corridor with 16 locations • There are four doors at positions: 2, 4, 7, 1 1 • The Robot initially doesn’t know where it is • The Robot is pushed ar around. After a push it can stay in the same location, move left or right. • The Robot has a Noisy y sensor telling whether it is in front of a door CPSC 322, Lecture 32 Slide 9

This scenario can be represented as… • Exam ample S Sto tochas asti tic Dyn ynam amics: when pushed, it stays in the same location p=0.2, moves one step left or right with equal probability P(Loc t + 1 | Loc t ) A. A. Loc t = 10 B. C.

This scenario can be represented as… • Exam ample S Sto tochas asti tic Dyn ynam amics: when pushed, it stays in the same location p=0.2, moves left or right with equal probability P(Loc t + 1 | Loc t ) P(Loc 1 ) CPSC 322, Lecture 32 Slide 1 1

This scenario can be represented as… Exam ample o of Noisy se y sensor telling whether P(O t | Loc t ) it is in front of a door . • If it is in front of a door P(O t = T) = .8 • If not in front of a door P(O t = T) = .1 CPSC 322, Lecture 32 Slide 12

Usefu ful i l infe ference in in H HMMs • Loc ocaliza zation on: Robot starts at an unknown location and it is pushed around t times. It wants to determine where it is • In In ge general: compute the posterior distribution over the current state given all evidence to date P(S t | O 0 … O t ) CPSC 322, Lecture 32 Slide 13

Exa xamp mple le : Robo bot Lo Local aliz izat atio ion • Suppose a robot wants to determine its location based on its actions and its sensor readings • Three actions: goRight, goLeft, Stay • This can be represented by an augmented HMM CPSC 322, Lecture 32 Slide 14

Robo bot Lo Local aliz izat atio ion Se Sensor an and d Dyn ynam amic ics M Mode del • Sam ample S Sensor Model (assume same as for pushed around) • Sam ample S Sto tochas asti tic Dyn ynam amics: P(Loc t + 1 | Action t , Loc t ) P(Loc t + 1 = L | Action t = goRight , Loc t = L) = 0.1 P(Loc t + 1 = L+1 | Action t = goRight , Loc t = L) = 0.8 P(Loc t + 1 = L + 2 | Action t = goRight , Loc t = L) = 0.074 P(Loc t + 1 = L’ | Action t = goRight , Loc t = L) = 0.002 for all other locations L’ • All location arithmetic is modulo 16 • The action goLeft works the same but to the left CPSC 322, Lecture 32 Slide 15

Dyn ynam amic ics Mo Mode del l Mo More De Detai ails ls • Sam ample S Sto tochas asti tic Dyn ynam amics: P(Loc t + 1 | Action, Loc t ) P(Loc t + 1 = L | Action t = goRight , Loc t = L) = 0.1 P(Loc t + 1 = L+1 | Action t = goRight , Loc t = L) = 0.8 P(Loc t + 1 = L + 2 | Action t = goRight , Loc t = L) = 0.074 P(Loc t + 1 = L’ | Action t = goRight , Loc t = L) = 0.002 for all other locations L’ CPSC 322, Lecture 32 Slide 16

Robo bot Lo Local aliz izat atio ion add addit itio ional al s sensor • Additi tional al Light S t Sensor: there is light coming through an opening at location 10 P (L t | Loc t ) • Info from th the tw two sensors is combined :“Sensor Fusion” CPSC 322, Lecture 32 Slide 17

Th The Rob obot ot st starts s at an unkn know own loc ocation on and m must st determine w where i it is The model appears to be too ambiguous • Sensors are too noisy • Dynamics are too stochastic to infer anything But inference actually works pretty well. You can check it at : http://www.cs.ubc.ca/spider/poole/demos/localization /localization.html You can use standard Bnet inference. However you typically take advantage of the fact that time moves forward (not in 322) CPSC 322, Lecture 32 Slide 18

Sa Samp mple le sc scenar ario io to to exp xplo lore re in in demo mo • Keep making observations without moving. What happens? • Then keep moving without making observations. What happens? • Assume you are at a certain position alternate moves and observations • …. CPSC 322, Lecture 32 Slide 19

HMMs have many other applications…. Na Natural Langu guage ge Proc ocess ssing: g: e.g., Speech Recognition • States: phoneme \ word • Observations : acoustic signal \ phoneme Bi Bioi oinfor ormatics: Gene Finding • States: coding / non-coding region • Observations: DNA Sequences Fo For these se prob oblems s the critical inference is: s: find the most likely sequence of states given a sequence of observations CPSC 322, Lecture 32 Slide 20

Mar arko kov v Mod odel els Simplest Possible Markov Chains Dynamic Bnet Add noisy Observations Hidden Markov Model about the state at time t Add Actions and Values Markov Decision (Rewards) Processes (MDPs) CPSC 322, Lecture 32 Slide 21

Learning Goals for today’s class Yo You c can an: • Specify the components of an Hidden Markov Model (HMM) • Justify and apply HMMs to Robot Localization Clarification on on on se secon ond LG G for or last st class ss You can an: • Justify and apply Markov Chains to compute the probability of a Natural Language sentence (NOT to estimate the conditional probs- slide 18) CPSC 322, Lecture 32 Slide 22

Ne Next xt wee eek Environ onment Sto tochas asti tic Dete terministi tic Prob oblem Arc Consiste tency Sear Se arch Constr trai aint t Var ars + Sat atisfac acti tion Constr trai aints ts SLS Sta tati tic Belief N Nets ts Logics Query Qu Var ar. Eliminat ation Sear arch Markov ov Chains s and HMMs Decision Nets ts Se Sequenti tial al STRIPS Var ar. Eliminat ation Planning Markov ov Decisio ion n Processe sses Sear arch Representa tati tion Val alue Ite terat ation Reas asoning CPSC 322, Lecture 32 Slide 23 Technique

Ne Next xt Cl Clas ass • One-off ff de decis isio ions (TextBook 9.2) • Sin ingle le S Stag age De Decis isio ion networks ( 9.2.1) Fin inal Thu, Jun Final Exam (2.5 hours) 29 at Room: BUCH A101 19:00 CPSC 322, Lecture 32 Slide 24