Linear Models for Regression Greg Mori - CMPT 419/726 Bishop PRML - PowerPoint PPT Presentation

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Models for Regression Greg Mori - CMPT 419/726 Bishop PRML Ch. 3

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Outline Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Regression

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Outline Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Regression

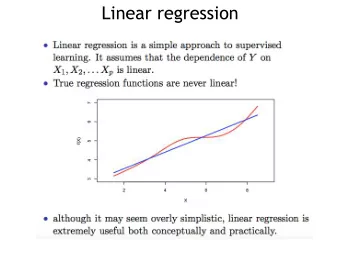
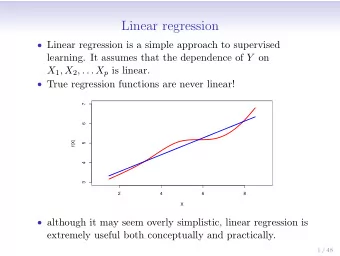
Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Regression • Given training set { ( x 1 , t 1 ) , . . . , ( x N , t N ) } • t i is continuous: regression • For now, assume t i ∈ R , x i ∈ R D • E.g. t i is stock price, x i contains company profit, debt, cash flow, gross sales, number of spam emails sent, . . .

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Outline Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Regression

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Functions • A function f ( · ) is linear if f ( α u + β v ) = α f ( u ) + β f ( v ) • Linear functions will lead to simple algorithms, so let’s see what we can do with them

✂☎✄✝✆ ✁ � Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Regression • Simplest linear model for regression y ( x , w ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w D x D • Remember, we’re learning w • Set w so that y ( x , w ) aligns with target value in training data

✂☎✄✝✆ ✁ � Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Regression • Simplest linear model for regression y ( x , w ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w D x D • Remember, we’re learning w • Set w so that y ( x , w ) aligns with target value in training data

� ✁ Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Regression • Simplest linear model for regression y ( x , w ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w D x D • Remember, we’re learning w • Set w so that y ( x , w ) aligns with target value in training data • This is a very simple model, limited in what it can do ✂☎✄✝✆ 1 0 −1 0 1

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Simplest linear model y ( x , w ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w D x D was linear in x ( ∗ ) and w • Linear in w is what will be important for simple algorithms • Extend to include fixed non-linear functions of data y ( x , w ) = w 0 + w 1 φ 1 ( x ) + w 2 φ 2 ( x ) + . . . + w M − 1 φ M − 1 ( x ) • Linear combinations of these basis functions also linear in parameters

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Simplest linear model y ( x , w ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w D x D was linear in x ( ∗ ) and w • Linear in w is what will be important for simple algorithms • Extend to include fixed non-linear functions of data y ( x , w ) = w 0 + w 1 φ 1 ( x ) + w 2 φ 2 ( x ) + . . . + w M − 1 φ M − 1 ( x ) • Linear combinations of these basis functions also linear in parameters

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Simplest linear model y ( x , w ) = w 0 + w 1 x 1 + w 2 x 2 + . . . + w D x D was linear in x ( ∗ ) and w • Linear in w is what will be important for simple algorithms • Extend to include fixed non-linear functions of data y ( x , w ) = w 0 + w 1 φ 1 ( x ) + w 2 φ 2 ( x ) + . . . + w M − 1 φ M − 1 ( x ) • Linear combinations of these basis functions also linear in parameters

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Bias parameter allows fixed offset in data y ( x , w ) = w 0 + w 1 φ 1 ( x ) + w 2 φ 2 ( x ) + . . . + w M − 1 φ M − 1 ( x ) ���� bias • Think of simple 1-D x : y ( x , w ) = + w 1 w 0 x ���� ���� intercept slope • For notational convenience, define φ 0 ( x ) = 1 : M − 1 � w j φ j ( x ) = w T φ ( x ) y ( x , w ) = j = 0

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Bias parameter allows fixed offset in data y ( x , w ) = w 0 + w 1 φ 1 ( x ) + w 2 φ 2 ( x ) + . . . + w M − 1 φ M − 1 ( x ) ���� bias • Think of simple 1-D x : y ( x , w ) = + w 1 w 0 x ���� ���� intercept slope • For notational convenience, define φ 0 ( x ) = 1 : M − 1 � w j φ j ( x ) = w T φ ( x ) y ( x , w ) = j = 0

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Bias parameter allows fixed offset in data y ( x , w ) = w 0 + w 1 φ 1 ( x ) + w 2 φ 2 ( x ) + . . . + w M − 1 φ M − 1 ( x ) ���� bias • Think of simple 1-D x : y ( x , w ) = + w 1 w 0 x ���� ���� intercept slope • For notational convenience, define φ 0 ( x ) = 1 : M − 1 � w j φ j ( x ) = w T φ ( x ) y ( x , w ) = j = 0

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Function for regression y ( x , w ) is non-linear function of x , but linear in w : M − 1 � w j φ j ( x ) = w T φ ( x ) y ( x , w ) = j = 0 • Polynomial regression is an example of this • Order M polynomial regression, φ j ( x ) =?

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Function for regression y ( x , w ) is non-linear function of x , but linear in w : M − 1 � w j φ j ( x ) = w T φ ( x ) y ( x , w ) = j = 0 • Polynomial regression is an example of this • Order M polynomial regression, φ j ( x ) =?

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Linear Basis Function Models • Function for regression y ( x , w ) is non-linear function of x , but linear in w : M − 1 � w j φ j ( x ) = w T φ ( x ) y ( x , w ) = j = 0 • Polynomial regression is an example of this • Order M polynomial regression, φ j ( x ) =? • φ j ( x ) = x j : y ( x , w ) = w 0 x 0 + w 1 x 1 + . . . + w M x M

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Basis Functions: Feature Functions • Often we extract features from x • An intuitve way to think of φ j ( x ) is as feature functions • E.g. Automatic CMPT726 project report grading system • x is text of report: In this project we apply the algorithm of Mori [2] to recognizing blue objects. We test this algorithm on pictures of you and I from my holiday photo collection. ... • φ 1 ( x ) is count of occurrences of Mori [ • φ 2 ( x ) is count of occurrences of of you and I • Regression grade y ( x , w ) = 20 φ 1 ( x ) − 10 φ 2 ( x )

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Basis Functions: Feature Functions • Often we extract features from x • An intuitve way to think of φ j ( x ) is as feature functions • E.g. Automatic CMPT726 project report grading system • x is text of report: In this project we apply the algorithm of Mori [2] to recognizing blue objects. We test this algorithm on pictures of you and I from my holiday photo collection. ... • φ 1 ( x ) is count of occurrences of Mori [ • φ 2 ( x ) is count of occurrences of of you and I • Regression grade y ( x , w ) = 20 φ 1 ( x ) − 10 φ 2 ( x )

Regression Linear Basis Function Models Loss Functions for Regression Finding Optimal Weights Regularization Bayesian Linear Basis Functions: Feature Functions • Often we extract features from x • An intuitve way to think of φ j ( x ) is as feature functions • E.g. Automatic CMPT726 project report grading system • x is text of report: In this project we apply the algorithm of Mori [2] to recognizing blue objects. We test this algorithm on pictures of you and I from my holiday photo collection. ... • φ 1 ( x ) is count of occurrences of Mori [ • φ 2 ( x ) is count of occurrences of of you and I • Regression grade y ( x , w ) = 20 φ 1 ( x ) − 10 φ 2 ( x )