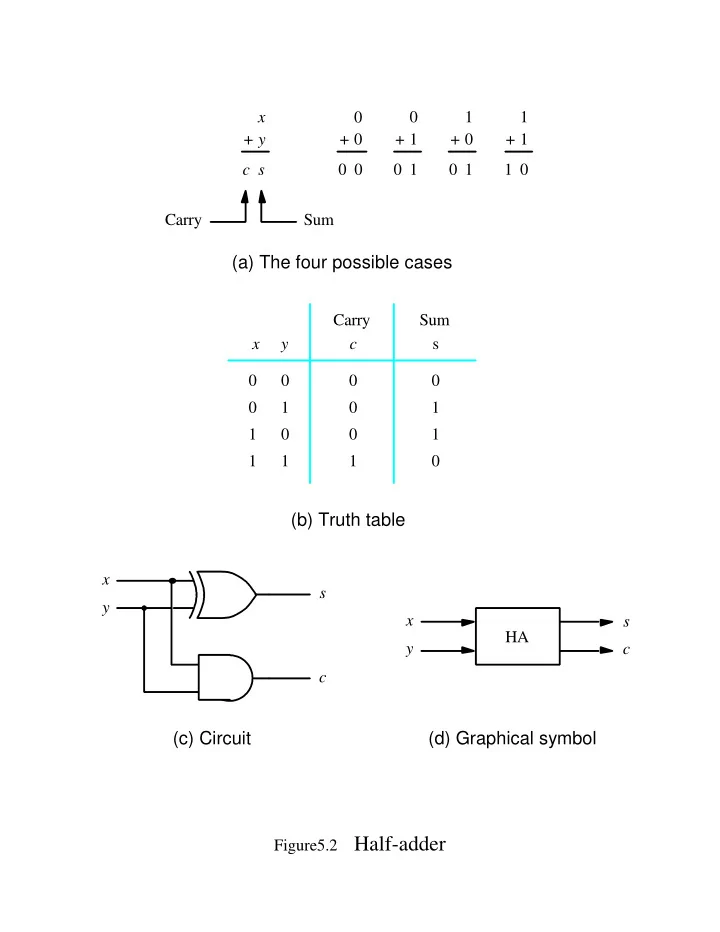
figure5 2 half adder
play

Figure5.2 Half-adder x i y i c 00 01 11 10 i 1 1 0 c i x - PDF document

Oct 31, 2023 •153 likes •232 views

x 0 0 1 1 + y + 0 + 1 + 0 + 1 c s 0 0 0 1 0 1 1 0 Carry Sum (a) The four possible cases Carry Sum x y c s 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 (b) Truth table x s y x s HA y c c (c) Circuit (d)

  1. x 0 0 1 1 + y + 0 + 1 + 0 + 1 c s 0 0 0 1 0 1 1 0 Carry Sum (a) The four possible cases Carry Sum x y c s 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 (b) Truth table x s y x s HA y c c (c) Circuit (d) Graphical symbol Figure5.2 Half-adder

  2. x i y i c 00 01 11 10 i 1 1 0 c i x i y c s i i + 1 i 1 1 1 0 0 0 0 0 0 0 1 0 1 s = x y c ⊕ ⊕ i i i i 0 1 0 0 1 0 1 1 1 0 x i y i 1 0 0 0 1 c 00 01 11 10 i 1 0 1 1 0 1 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 (a) Truth table c = x i y + x i c + y i c i + 1 i i i (b) Karnaugh maps x i y s i i c i c i + 1 (c) Circuit Figure5.4 Full-adder

  3. A : a a 7 0 x x y y 7 0 7 0 c 7 s s 7 0 0 x x x y y y 8 7 0 8 7 0 c 8 s s 8 0 = 3 : P A P P P 9 8 0 (a) Naive approach A : a a 7 0 0 0 x x 1 x y y y 8 0 8 7 0 c 8 s s 8 0 : P = 3 A P P P 9 8 0 (b) Efficient design Figure5.7 Circuit that multiplies an 8-bit unsigned number by 3

  4. Multiplicand M (14) 1 1 1 0 Multiplier Q (11) 1 0 1 1 × 1 1 1 0 1 1 1 0 0 0 0 0 1 1 1 0 Product P (154) 1 0 0 1 1 0 1 0 (a) Multiplication by hand Multiplicand M (11) 1 1 1 0 Multiplier Q (14) × 1 0 1 1 Partial product 0 1 1 1 0 + 1 1 1 0 Partial product 1 1 0 1 0 1 + 0 0 0 0 Partial product 2 0 1 0 1 0 + 1 1 1 0 Product P (154) 1 0 0 1 1 0 1 0 (b) Multiplication for implementation in hardware Figure5.32 Multiplication of unsigned numbers

  5. 0 m m m m 3 2 1 0 q 0 0 PP1 q 1 q 2 0 PP2 q 3 0 p p p p p p p p 7 6 5 4 3 2 1 0 (a) Structure of the circuit m m k + 1 k Bit of PPi m k q 0 q q j 1 c c c c FA FA out out in in (b) A block in the top row (c) A block in the bottom two rows Figure5.33 A 4 x 4 multiplier circuit

  6. Multiplicand M (+14) 0 1 1 1 0 x Multiplier Q (+11) 0 1 0 1 1 Partial product 0 0 0 0 1 1 1 0 + 0 0 1 1 1 0 Partial product 1 0 0 1 0 1 0 1 + 0 0 0 0 0 0 Partial product 2 0 0 0 1 0 1 0 + 0 0 1 1 1 0 Partial product 3 0 0 1 0 0 1 1 + 0 0 0 0 0 0 Product P (+154) 0 0 1 0 0 1 1 0 1 0 (a) Positive multiplicand Multiplicand M ( 14) – 1 0 0 1 0 Multiplier Q (+11) 0 1 0 1 1 × Partial product 0 1 1 1 0 0 1 0 + 1 1 0 0 1 0 Partial product 1 1 1 0 1 0 1 1 0 0 0 0 0 0 + Partial product 2 1 1 1 0 1 0 1 + 1 1 0 0 1 0 Partial product 3 1 1 0 1 1 0 0 + 0 0 0 0 0 0 – Product P ( 154) 1 1 0 1 1 0 0 1 1 0 (b) Negative multiplicand Figure5.34 Multiplication of signed numbers

  7. Table 5.4 The seven-bit ASCII code

Download Presentation
Download Policy: The content available on the website is offered to you 'AS IS' for your personal information and use only. It cannot be commercialized, licensed, or distributed on other websites without prior consent from the author. To download a presentation, simply click this link. If you encounter any difficulties during the download process, it's possible that the publisher has removed the file from their server.

Recommend

ex start small with a 1-bit (half) adder A B Carry out Sum A 0 0 Sum 0 1 B 1 0 1 1

ex start small with a 1-bit (half) adder A B Carry out Sum A 0 0 Sum 0 1 B 1 0 1 1

Addition: ex start small with a 1-bit (half) adder A B Carry out Sum A 0 0 Sum 0 1 B 1 0 1 1 Carry out Carry in ex 1-bit full adder A + Sum B Carry out n-bit addition: Sum i = A i + B i + CarryOut i-1 Need a bigger adder!

328 views • 12 slides
Combinatorial networks- II Digital Systems M 1 Adder Lets see the truth table of a

Combinatorial networks- II Digital Systems M 1 Adder Lets see the truth table of a

Combinatorial networks- II Digital Systems M 1 Adder Lets see the truth table of a combinatorial network whose output values correspond to the numerical values of a 2-bit adder (Half Adder) ab Sum Carry 00 0

852 views • 64 slides
Outline Introduction to CMOS VLSI Single-bit Addition Design Carry-Ripple Adder

Outline Introduction to CMOS VLSI Single-bit Addition Design Carry-Ripple Adder

Outline Introduction to CMOS VLSI Single-bit Addition Design Carry-Ripple Adder Carry-Skip Adder Carry-Lookahead Adder Lecture 11: Carry-Select Adder Adders Carry-Increment Adder Tree Adder David Harris Harvey Mudd

193 views • 8 slides
Lesson 7 Combinational Logic Circuits Concepts Introduced Adders Multiplexers

Lesson 7 Combinational Logic Circuits Concepts Introduced Adders Multiplexers

Lesson 7 Combinational Logic Circuits Concepts Introduced Adders Multiplexers Decoders basic Arithmetic/Logic Unit Review Half-Adder A half adder takes two inputs, a and b, and generates two outputs, the carry and the sum.

354 views • 32 slides
FAST TWO-OPERAND ADDITION A. Conventional number system. Carry-propagate adders (CPA)

FAST TWO-OPERAND ADDITION A. Conventional number system. Carry-propagate adders (CPA)

1 FAST TWO-OPERAND ADDITION A. Conventional number system. Carry-propagate adders (CPA) Switched carry-ripple adder Carry-skip adder Carry-lookahead adder Prefix adder Carry-select adder and conditional-sum adder

921 views • 57 slides
ex Addition: 1-bit half adder A + Sum B Carry out Carry A B Sum out 0 0 A 0 1 Sum

ex Addition: 1-bit half adder A + Sum B Carry out Carry A B Sum out 0 0 A 0 1 Sum

ex Addition: 1-bit half adder A + Sum B Carry out Carry A B Sum out 0 0 A 0 1 Sum B 1 0 1 1 Carry out Carry in ex Addition: 1-bit full adder A + Sum B Carry out Carry Carry Carry in A B Sum in out 0 0 0 A 0

343 views • 12 slides
Problem 1 Design a Verilog 16-bit adder module module adder (A, B, sum); input [15:0] A, B;

Problem 1 Design a Verilog 16-bit adder module module adder (A, B, sum); input [15:0] A, B;

Problem 1 Design a Verilog 16-bit adder module module adder (A, B, sum); input [15:0] A, B; output [15:0] sum; assign sum = A + B; endmodule Problem 1 Design a Verilog 16-bit adder module module adder (A, B, sum); input [15:0] A,

653 views • 22 slides
CSE 140 Lecture 13 Standard Combinational Modules CK Cheng CSE Dept. UC San Diego Some slides

CSE 140 Lecture 13 Standard Combinational Modules CK Cheng CSE Dept. UC San Diego Some slides

CSE 140 Lecture 13 Standard Combinational Modules CK Cheng CSE Dept. UC San Diego Some slides from Harris and Harris 1 Part III. Standard Modules Interconnect Operators. Representation of numbers Adders 1. Full Adder 2. Half Adder 3.

689 views • 45 slides
Continuations Control flow of Web applications Michel Schinz 20070504 The adder

Continuations Control flow of Web applications Michel Schinz 20070504 The adder

Continuations Control flow of Web applications Michel Schinz 20070504 The adder application The adder Web application Lets assume that we want to take our adder application and turn it into a Web application, with the requirement

463 views • 7 slides
I'm Etienne React trainer & dev & consultant @LeReacteurIO A Binary adder written

I'm Etienne React trainer & dev & consultant @LeReacteurIO A Binary adder written

Hi I'm Etienne React trainer & dev & consultant @LeReacteurIO A Binary adder written with TypeScript types only Binary what ? An adder is a digital circuit that performs addition of numbers. Yes, we are just trying to

444 views • 32 slides
Learning Outcomes I understand what gates are used to design half and full adders Unit 12

Learning Outcomes I understand what gates are used to design half and full adders Unit 12

12.1 12.2 Learning Outcomes I understand what gates are used to design half and full adders Unit 12 I can build larger arithmetic circuits from smaller building blocks Adders & Arithmetic Circuits 12.3 12.4 Adder Intro

278 views • 10 slides
5. Simulate the n-bit modular adder/subtracter architecture The modular adder/subtracter performs

5. Simulate the n-bit modular adder/subtracter architecture The modular adder/subtracter performs

Summer School on Real-world Crypto and Privacy Hardware tutorial June 14, 2018, ibenik, Croatia Nele Mentens (KU Leuven) Pedro Maat Costa Massolino (Radboud University) TUTORIAL INSTRUCTIONS In this tutorial, we will design and simulate a

74 views • 4 slides
TV VA Brightness Adder 09/04/19 EPA Luminance Requirements For products with a luminance in

TV VA Brightness Adder 09/04/19 EPA Luminance Requirements For products with a luminance in

TV VA Brightness Adder 09/04/19 EPA Luminance Requirements For products with a luminance in the Brightest Selectable Preset Picture Setting (the greater value of L DEFAULT_RETAIL or L BRIGHTEST_HOME) less than 350 cd/m2, luminance in the

412 views • 6 slides
Regulating attention We hear half of what is said (50%) We listen to half of that

Regulating attention We hear half of what is said (50%) We listen to half of that

Listening well-while attending a Yannis Theodorakis lecture Regulating attention We hear half of what is said (50%) We listen to half of that (25%) and concentration We understand half of them (12.5%) We believe half

457 views • 13 slides
Behavioral Modeling Using continuous assignments ISE can build you a nice adder Easier

Behavioral Modeling Using continuous assignments ISE can build you a nice adder Easier

Verilog Synthesis Examples CS/EE 3710 Fall 2010 Mostly from CMOS VLSI Design by Weste and Harris Behavioral Modeling Using continuous assignments ISE can build you a nice adder Easier than specifying your own 1 Bitwise Operators

471 views • 19 slides
Continuations Michel Schinz 20070504 Control flow of Web applications The adder

Continuations Michel Schinz 20070504 Control flow of Web applications The adder

Continuations Michel Schinz 20070504 Control flow of Web applications The adder application The following Scheme program asks for two numbers, and displays their sum assuming the obvious definitions for prompt-int and display-int :

748 views • 42 slides
Formal Specification and Verification of the FM9001 Microprocessor Using the DE System Cuong Chau

Formal Specification and Verification of the FM9001 Microprocessor Using the DE System Cuong Chau

Formal Specification and Verification of the FM9001 Microprocessor Using the DE System Cuong Chau ckcuong@cs.utexas.edu Department of Computer Science The University of Texas at Austin May 23, 2017 Cuong Chau (UT Austin) FM9001 Specification

883 views • 50 slides
Functions, Abstraction & Faculty of Computer Science Dalhousie University Recursion Winter

Functions, Abstraction & Faculty of Computer Science Dalhousie University Recursion Winter

CSCI 2132: Software Development Norbert Zeh Functions, Abstraction & Faculty of Computer Science Dalhousie University Recursion Winter 2019 Building Abstractions Large projects are built in layers of abstraction! Example: Computer We

941 views • 66 slides
Lecture 2 Review Path Intergrals over Complex Plane Let : ( *

Lecture 2 Review Path Intergrals over Complex Plane Let : ( *

Lecture 2 Review Path Intergrals over Complex Plane Let : ( * = ? ( ) Lecture 2 Review Question #1: Express XOR using only NAND and NOT gates A A B B Y Y A A B B rgans&theorem!&

775 views • 16 slides
Digital Logic CombinaAonal Circuits 2 Homework Notes

Digital Logic CombinaAonal Circuits 2 Homework Notes

Computer Systems and Networks ECPE 170 Jeff Shafer University of the Pacific Digital Logic CombinaAonal Circuits 2 Homework Notes

452 views • 27 slides
Digitalteknik & Datorarkitektur vren 2009 Rkna med grindar Frelsning 2 mndag 23

Digitalteknik & Datorarkitektur vren 2009 Rkna med grindar Frelsning 2 mndag 23

Digitalteknik & Datorarkitektur vren 2009 Rkna med grindar Frelsning 2 mndag 23 mars karl.marklund@it.uu.se Gates and Boolean Algebra Some logical functions for two variables. x y x AND y x OR y x XOR y 0 0 0 0 0 0 1

484 views • 32 slides
Carbon Nanotube Imperfection-Immune Digital VLSI Subhasish Mitra Robust Systems Group

Carbon Nanotube Imperfection-Immune Digital VLSI Subhasish Mitra Robust Systems Group

Carbon Nanotube Imperfection-Immune Digital VLSI Subhasish Mitra Robust Systems Group Department of EE & Department of CS Stanford University H. Chen, J. Deng, A. Hazeghi, A. Lin, N. Patil, M. Shulaker, L. Wei, H. Wei, Prof. H.-S. P. Wong,

731 views • 60 slides
Normal-Conducting Photoinjector for High Power CW FEL Sergey Kurennoy, LANL, Los Alamos, NM An RF

Normal-Conducting Photoinjector for High Power CW FEL Sergey Kurennoy, LANL, Los Alamos, NM An RF

LA-UR-04-2768,-5617,-5808, & 05-3172 www.arXiv.org: physics/0404109 Normal-Conducting Photoinjector for High Power CW FEL Sergey Kurennoy, LANL, Los Alamos, NM An RF photoinjector capable of producing high continuous average current with low

404 views • 25 slides
Disclosures Disclosures Fractures: A. Schwartz A. Schwartz Epidemiology and Risk Factors

Disclosures Disclosures Fractures: A. Schwartz A. Schwartz Epidemiology and Risk Factors

July 2012 CME (35 minutes) 6/13/2013 Disclosures Disclosures Fractures: A. Schwartz A. Schwartz Epidemiology and Risk Factors Consulting: Merck Ann V. Schwartz, PhD Department of Epidemiology and Biostatistics UCSF Epidemiology of

487 views • 11 slides

More recommend