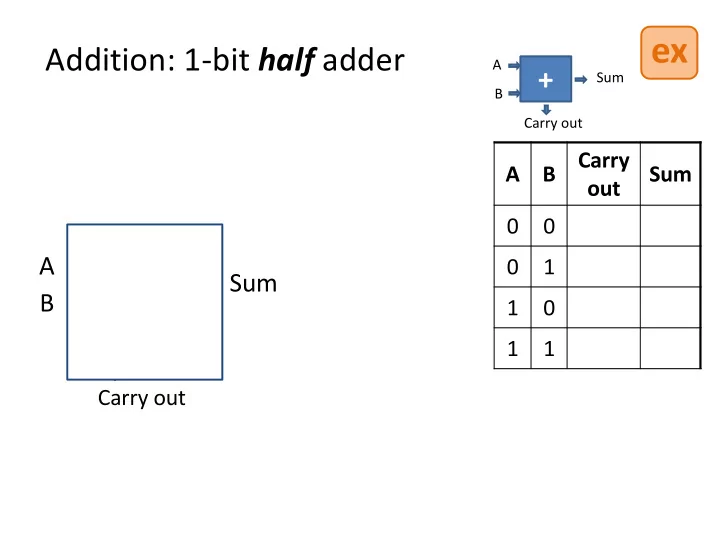

ex Addition: 1-bit half adder A + Sum B Carry out Carry A B Sum out 0 0 A 0 1 Sum B 1 0 1 1 Carry out
Carry in ex Addition: 1-bit full adder A + Sum B Carry out Carry Carry Carry in A B Sum in out 0 0 0 A 0 0 1 Sum B 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 Carry out 1 1 1
Addition: n -bit ripple-carry adder Carry in 0 A 0 + Sum 0 B 0 Carry in A 1 + Sum 1 B 1 A Sum A 2 + B Sum 2 B 2 … A n-1 + Sum n-1 B n-1 Carry out Carry out n-1 There are faster, more complicated ways too…
Processor Components Abstraction! 4 1 3 2 Instruction ALU Registers Memory Fetch and Decode
1 Arithmetic Logic Unit (ALU) a few bits Condition Codes (sign, overflow, carry-out, zero) word Operand A ALU words Result Operand B Operation a few bits Hardware unit for arithmetic and bitwise operations.
ex 1-bit ALU for bitwise operations Build an n-bit ALU from n 1-bit ALUs. Each bit i in the result is computed from the corresponding bit i in the two inputs. Op A B Result 0 0 0 Operation 0 0 1 A 0 1 0 0 MUX 0 1 1 Result 1 0 0 B 1 1 0 1 1 1 0 1 1 1
1-bit ALU Operation Carry in 2 A 0 MUX Result 1 Sum + 2 B Carry out
Carry in 2 Operation A 0 n-bit ripple carry adder 0 Result 0 MUX 1 Carry in Sum + B 0 2 A 0 + Sum 0 B 0 A 1 0 Result 1 MUX A 1 1 + Sum 1 Sum + B 1 2 B 1 A 2 + .... n-bit ALU … Sum 2 B 2 … A n-1 0 Result n-1 MUX A n-1 + 1 Sum n-1 Sum + B n-1 B n-1 2 Carry out Carry out
Carry in 2 Operation ALU conditions A 0 0 Result 0 MUX 1 Extra ALU outputs Sum + B 0 2 describing properties of result. A 1 Zero Flag: ex 0 Result 1 MUX 1 if result is 00...0 else 0 1 + Sum Sign Flag: ex B 1 2 1 if result is negative else 0 .... … Carry Flag: 1 if carry out else 0 (Signed) Overflow Flag: A n-1 0 Result n-1 1 if signed overflow else 0 MUX 1 Sum + B n-1 2 Implement these. Carry out
Operation 2 Add subtraction A 0 0 Result 0 MUX 1 How can we control ALU inputs B 0 + 0 2 or add minimal new logic 1 to compute A-B ? A 1 0 Result 1 MUX 1 + B 1 0 2 1 .... .... … A n-1 0 Result n-1 MUX 1 + B n-1 0 2 1 Carry out
Negate B Operation Invert A A NAND B 2 A 0 0 0 1 Result 0 MUX 1 A NOR B + B 0 0 2 1 A 1 0 0 1 A<B Result 1 MUX 1 + B 1 0 2 1 A==B .... .... .... … A n-1 0 0 1 Result n-1 MUX How can we control ALU inputs 1 or add minimal new logic + B n-1 0 ex 2 to compute each? 1 Carry out
Abstraction! Controlling the ALU Condition Codes ALU control lines Function 0000 AND Operand A 0001 OR ALU Result 0010 add Operand B 0110 subtract 1100 NOR Control Lines
Recommend
More recommend