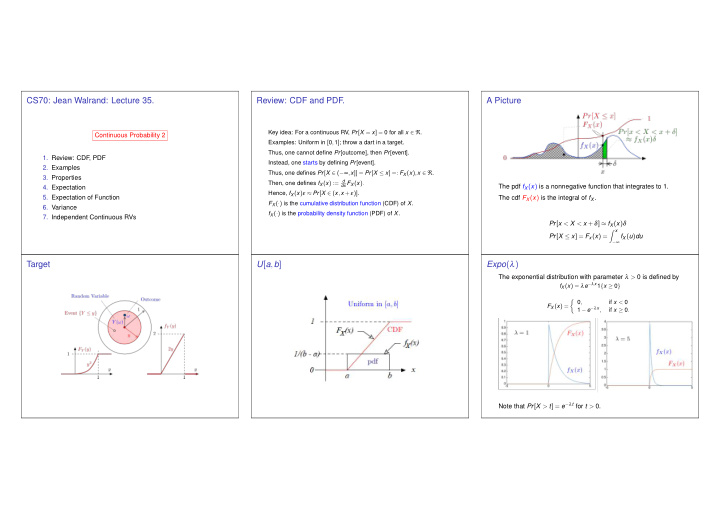



CS70: Jean Walrand: Lecture 35. Review: CDF and PDF. A Picture Key idea: For a continuous RV, Pr [ X = x ] = 0 for all x ∈ ℜ . Continuous Probability 2 Examples: Uniform in [ 0 , 1 ] ; throw a dart in a target. Thus, one cannot define Pr [ outcome ] , then Pr [ event ] . 1. Review: CDF , PDF Instead, one starts by defining Pr [ event ] . 2. Examples Thus, one defines Pr [ X ∈ ( − ∞ , x ]] = Pr [ X ≤ x ] =: F X ( x ) , x ∈ ℜ . 3. Properties Then, one defines f X ( x ) := d dx F X ( x ) . The pdf f X ( x ) is a nonnegative function that integrates to 1. 4. Expectation Hence, f X ( x ) ε ≈ Pr [ X ∈ ( x , x + ε )] . 5. Expectation of Function The cdf F X ( x ) is the integral of f X . F X ( · ) is the cumulative distribution function (CDF) of X . 6. Variance f X ( · ) is the probability density function (PDF) of X . 7. Independent Continuous RVs Pr [ x < X < x + δ ] ≈ f X ( x ) δ � x Pr [ X ≤ x ] = F x ( x ) = − ∞ f X ( u ) du Target U [ a , b ] Expo ( λ ) The exponential distribution with parameter λ > 0 is defined by f X ( x ) = λ e − λ x 1 { x ≥ 0 } � 0 , if x < 0 F X ( x ) = 1 − e − λ x , if x ≥ 0 . Note that Pr [ X > t ] = e − λ t for t > 0.
Some Properties More Properties Some More Properties 1. Expo is memoryless. Let X = Expo ( λ ) . Then, for s , t > 0, 3. Scaling Uniform. Let X = U [ 0 , 1 ] and Y = a + bX where b > 0. Pr [ X > t + s ] 4. Scaling pdf. Let f X ( x ) be the pdf of X and Y = a + bX where Then, Pr [ X > t + s | X > s ] = Pr [ X > s ] b > 0. Then Pr [ a + bX ∈ ( y , y + δ )] = Pr [ X ∈ ( y − a , y + δ − a e − λ ( t + s ) Pr [ Y ∈ ( y , y + δ )] = )] = e − λ t Pr [ a + bX ∈ ( y , y + δ )] = Pr [ X ∈ ( y − a , y + δ − a = b b Pr [ Y ∈ ( y , y + δ )] = )] e − λ s b b , y − a b δ , for 0 < y − a Pr [ X ∈ ( y − a + δ b )] = 1 = Pr [ X > t ] . = < 1 b )] = f X ( y − a Pr [ X ∈ ( y − a , y − a + δ ) δ b b b = b . b b b 1 ‘Used is a good as new.’ = b δ , for a < y < a + b . Now, the left-hand side is f Y ( y ) δ . Hence, 2. Scaling Expo . Let X = Expo ( λ ) and Y = aX for some a > 0. Then Thus, f Y ( y ) = 1 b for a < y < a + b . Hence, Y = U [ a , a + b ] . f Y ( y ) = 1 bf X ( y − a Pr [ Y > t ] = Pr [ aX > t ] = Pr [ X > t / a ] ) . b e − λ ( t / a ) = e − ( λ / a ) t = Pr [ Z > t ] for Z = Expo ( λ / a ) . = Replacing b by b − a we see that, if X = U [ 0 , 1 ] , then Y = a +( b − a ) X is U [ a , b ] . Thus, a × Expo ( λ ) = Expo ( λ / a ) . Also, Expo ( λ ) = 1 λ Expo ( 1 ) . Expectation Examples of Expectation Examples of Expectation Definition: The expectation of a random variable X with pdf f ( x ) is 3. X = Expo ( λ ) . Then, f X ( x ) = λ e − λ x 1 { x ≥ 0 } . Thus, defined as � ∞ E [ X ] = − ∞ xf X ( x ) dx . � ∞ � ∞ 0 x λ e − λ x dx = − 0 xde − λ x . E [ X ] = 1. X = U [ 0 , 1 ] . Then, f X ( x ) = 1 { 0 ≤ x ≤ 1 } . Thus, Justification: Say X = n δ w.p. f X ( n δ ) δ for n ∈ Z . Then, � ∞ � 1 � ∞ � x 2 0 = 1 � 1 Recall the integration by parts formula: E [ X ] = ∑ ( n δ ) Pr [ X = n δ ] = ∑ E [ X ] = − ∞ xf X ( x ) dx = 0 x . 1 dx = 2 . ( n δ ) f X ( n δ ) δ = − ∞ xf X ( x ) dx . 2 � b � b n n � b � a u ( x ) dv ( x ) = u ( x ) v ( x ) a − a v ( x ) du ( x ) � g ( x ) dx ≈ ∑ n g ( n δ ) δ . Choose Indeed, for any g , one has � b 2. X = distance to 0 of dart shot uniformly in unit circle. Then g ( x ) = xf X ( x ) . = u ( b ) v ( b ) − u ( a ) v ( a ) − a v ( x ) du ( x ) . f X ( x ) = 2 x 1 { 0 ≤ x ≤ 1 } . Thus, � ∞ � 1 � 2 x 3 0 = 2 Thus, � 1 E [ X ] = − ∞ xf X ( x ) dx = 0 x . 2 xdx = 3 . 3 � ∞ � ∞ 0 xde − λ x [ xe − λ x ] ∞ 0 e − λ x dx = 0 − � ∞ 0 − 0 + 1 0 de − λ x = − 1 = λ . λ Hence, E [ X ] = 1 λ .
Multiple Continuous Random Variables Example of Continuous ( X , Y ) Independent Continuous Random Variables Pick a point ( X , Y ) uniformly in the unit circle. Definition: The continuous RVs X and Y are independent if One defines a pair ( X , Y ) of continuous RVs by specifying f X , Y ( x , y ) Pr [ X ∈ A , Y ∈ B ] = Pr [ X ∈ A ] Pr [ Y ∈ B ] , ∀ A , B . for x , y ∈ ℜ where Theorem: The continuous RVs X and Y are independent if and only f X , Y ( x , y ) dxdy = Pr [ X ∈ ( x , x + dx ) , Y ∈ ( y + dy )] . if f X , Y ( x , y ) = f X ( x ) f Y ( y ) . The function f X , Y ( x , y ) is called the joint pdf of X and Y . Example: Choose a point ( X , Y ) uniformly in the set A ⊂ ℜ 2 . Then Proof: As in the discrete case. Definition: The continuous RVs X 1 ,..., X n are mutually independent f X , Y ( x , y ) = 1 π 1 { x 2 + y 2 ≤ 1 } . | A | 1 { ( x , y ) ∈ A } Thus, f X , Y ( x , y ) = 1 if Consequently, Pr [ X 1 ∈ A 1 ,..., X n ∈ A n ] = Pr [ X 1 ∈ A 1 ] ··· Pr [ X n ∈ A n ] , ∀ A 1 ,..., A n . where | A | is the area of A . Pr [ X > 0 , Y > 0 ] = 1 Interpretation. Think of ( X , Y ) as being discrete on a grid with mesh 4 Theorem: The continuous RVs X 1 ,..., X n are mutually independent if size ε and Pr [ X = m ε , Y = n ε ] = f X , Y ( m ε , n ε ) ε 2 . Pr [ X < 0 , Y > 0 ] = 1 and only if 4 Extension: X = ( X 1 ,..., X n ) with f X ( x ) . Pr [ X 2 + Y 2 ≤ r 2 ] = r 2 f X ( x 1 ,..., x n ) = f X 1 ( x 1 ) ··· f X n ( x n ) . Pr [ X > Y ] = 1 2 . Proof: As in the discrete case. Examples of Independent Continuous RVs Expectation of Function of RVs Examples of Expectation of Function � ∞ Recall: E [ h ( X )] = − ∞ h ( x ) f X ( x ) dx . 1. Minimum of Independent Expo . Let X = Expo ( λ ) and Definitions: (a) The expectation of a function of a random variable is Y = Expo ( µ ) be independent RVs. 1. Let X = U [ 0 , 1 ] . Then defined as � ∞ Recall that Pr [ X > u ] = e − λ u . Then � 1 � x n + 1 1 � 1 E [ h ( X )] = − ∞ h ( x ) f X ( x ) dx . E [ X n ] = = 0 x n dx = 0 = n + 1 . n + 1 Pr [ min { X , Y } > u ] = Pr [ X > u , Y > u ] = Pr [ X > u ] Pr [ Y > u ] e − λ u × e − µ u = e − ( λ + µ ) u . = (b) The expectation of a function of multiple random variables is 2. Let X = U [ 0 , 1 ] and θ > 0. Then defined as � 1 � � This shows that min { X , Y } = Expo ( λ + µ ) . � 1 0 = sin ( θ ) E [ h ( X )] = ··· h ( x ) f X ( x ) dx 1 ··· dx n . � 1 E [ cos ( θ X )] = 0 cos ( θ x ) dx = θ sin ( θ x ) . θ Thus, the minimum of two independent exponentially distributed RVs is exponentially distributed. Justification: Say X = n δ w.p. f X ( n δ ) δ . Then, 3. Let X = Expo ( λ ) . Then 2. Minimum of Independent U [ 0 , 1 ] . Let X , Y = [ 0 , 1 ] be � ∞ � ∞ � ∞ E [ h ( X )] = ∑ h ( n δ ) Pr [ X = n δ ] = ∑ independent RVs. Let also Z = min { X , Y } . What is f Z ? h ( n δ ) f X ( n δ ) δ = − ∞ h ( x ) f X ( x ) dx . E [ X n ] 0 x n λ e − λ x dx = − 0 x n de − λ x = n n One has � ∞ x n e − λ x � ∞ 0 e − λ x dx n Pr [ Z > u ] = Pr [ X > u ] Pr [ Y > u ] = ( 1 − u ) 2 . � g ( x ) dx ≈ ∑ n g ( n δ ) δ . Choose � = − 0 + Indeed, for any g , one has � ∞ Thus F Z ( u ) = Pr [ Z ≤ u ] = 1 − ( 1 − u ) 2 . n 0 x n − 1 λ e − λ x dx = n g ( x ) = h ( x ) f X ( x ) . λ E [ X n − 1 ] . = λ Hence, f Z ( u ) = d du F Z ( u ) = 2 ( 1 − u ) , u ∈ [ 0 , 1 ] . In particular, The case of multiple RVs is similar. � 1 � 1 Since E [ X 0 ] = 1, this implies by induction that E [ X n ] = n ! 0 2 u ( 1 − u ) du = 2 1 2 − 2 1 3 = 1 λ n . E [ Z ] = 0 uf Z ( u ) du = 3 .
Linearity of Expectation Expectation of Product of Independent RVs Variance Theorem Expectation is linear. Definition: The variance of a continuous random variable X is defined as Proof: ‘As in the discrete case.’ Theorem If X , Y , X are mutually independent, then Example 1: X = U [ a , b ] . Then var [ X ] = E (( X − E ( X )) 2 ) = E ( X 2 ) − ( E ( X )) 2 . 1 E [ XYZ ] = E [ X ] E [ Y ] E [ Z ] . (a) f X ( x ) = b − a 1 { a ≤ x ≤ b } . Thus, � b Example 1: X = U [ 0 , 1 ] . Then � x 2 1 1 a = a + b � b E [ X ] = a x b − adx = . Proof: Same as discrete case. b − a 2 2 var [ X ] = E [ X 2 ] − E [ X ] 2 = 1 3 − 1 4 = 1 12 . Example: Let X , Y , Z be mutually independent and U [ 0 , 1 ] . Then (b) X = a +( b − a ) Y , Y = U [ 0 , 1 ] . Hence, E [ X 2 + 4 Y 2 + 9 Z 2 + 4 XY + 6 XZ + 12 YZ ] E [( X + 2 Y + 3 Z ) 2 ] = Example 2: X = Expo ( λ ) . Then E [ X ] = λ − 1 and E [ X 2 ] = 2 / ( λ 2 ) . E [ X ] = a +( b − a ) E [ Y ] = a + b − a = a + b 1 3 + 41 3 + 91 3 + 41 2 + 61 1 2 + 121 1 1 . = Hence, var [ X ] = 1 / ( λ 2 ) . 2 2 2 2 2 2 14 3 + 22 = 4 ≈ 10 . 17 . Example 2: X , Y are U [ 0 , 1 ] . Then Example 3: Let X , Y , Z be independent. Then E [ 3 X − 2 Y + 5 ] = 3 E [ X ] − 2 E [ Y ]+ 5 = 31 2 − 21 var [ X + Y + Z ] = var [ X ]+ var [ Y ]+ var [ Z ] , 2 + 5 = 5 . 5 . as in the discrete case. Summary Continuous Probability 2 1. pdf: Pr [ X ∈ ( x , x + δ ]] = f X ( x ) δ . � x 2. CDF: Pr [ X ≤ x ] = F X ( x ) = − ∞ f X ( y ) dy . 3. U [ a , b ] , Expo ( λ ) , target. � ∞ 4. Expectation: E [ X ] = − ∞ xf X ( x ) dx . � ∞ 5. Expectation of function: E [ h ( X )] = − ∞ h ( x ) f X ( x ) dx . 6. Variance: var [ X ] = E [( X − E [ X ]) 2 ] = E [ X 2 ] − E [ X ] 2 . 7. f X ( x ) dx 1 ··· dx n = Pr [ X 1 ∈ ( x 1 , x 1 + dx 1 ) ,..., X n ∈ ( x n , x n + dx n )] . 8. X 1 ,..., X n are mutually independent iff f X = f X 1 ×···× f X n . 9. X mutually independent ⇒ E [ X 1 ··· X n ] = E [ X 1 ] ··· E [ X n ] . � ··· � h ( x ) f X ( x ) dx 1 ··· dx n . 10. E [ h ( X )] = 11. Expectation is linear.
Recommend
More recommend