-4 -2 0 in 2 r, E 10 Erro 15 x 0 In-sample 20 x 1 25 - PowerPoint PPT Presentation

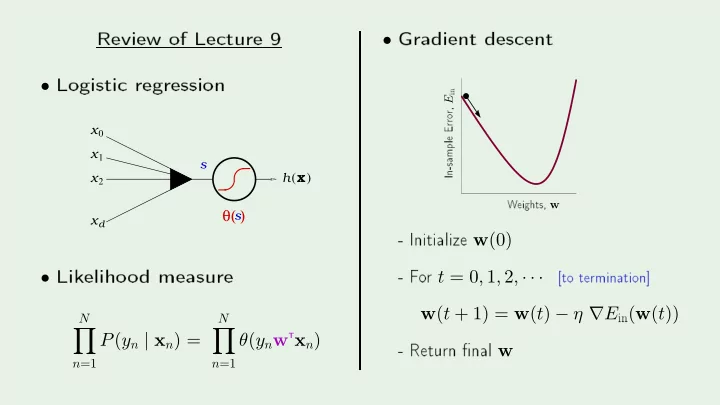
PSfrag repla ements Review of Le ture 9 Gradient des ent -10 -8 Logisti regression -6 • -4 -2 0 • in 2 r, E 10 Erro 15 x 0 In-sample 20 x 1 25 s W eights, w ( ) - Initialize w (0) x h x 2 θ( ) - F o r t = 0 , 1 , 2 , · · · [to termination℄ Lik eliho o d measure s x d in ( w ( t )) T x n ) • - Return �nal w w ( t + 1) = w ( t ) − η ∇ E N N � � P ( y n | x n ) = θ ( y n w n =1 n =1

Lea rning F rom Data Y aser S. Abu-Mostafa Califo rnia Institute of T e hnology Le ture 10 : Neural Net w o rks Sp onso red b y Calte h's Provost O� e, E&AS Division, and IST Thursda y , Ma y 3, 2012 •

Outline Sto hasti gradient des ent • Neural net w o rk mo del • Ba kp ropagation algo rithm • Creato r: Y aser Abu-Mostafa - LFD Le ture 10 2/21 M � A L

Sto hasti gradient des ent e GD minimizes: in ( w ) = 1 T x n ) ← in logisti regression N � � � h ( x n ) , y n E N � �� � n =1 b y iterative ln ( 1+ e − yn w steps along −∇ E : − in in ( w ) ∆ w = − η ∇ E is based on all examples ( x n , y n ) in � bat h � GD ∇ E Creato r: Y aser Abu-Mostafa - LFD Le ture 10 3/21 M � A L

The sto hasti asp e t Pi k one ( x n , y n ) at a time. Apply GD to e � � �A verage� dire tion: −∇ e −∇ e h ( x n ) , y n N = 1 � � � �� � � in h ( x n ) , y n h ( x n ) , y n E n N n =1 randomized version of GD = −∇ E sto hasti gradient des ent (SGD) Creato r: Y aser Abu-Mostafa - LFD Le ture 10 4/21 M � A L

PSfrag repla ements Bene�ts of SGD 1 2 1. heap er omputation 3 4 5 2. randomization 6 0 0.05 3. simple in 0.1 E W eights, w 0.15 Rule of thumb: randomization helps w o rks η = 0 . 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 10 5/21 M � A L

SGD in a tion Rememb er movie ratings? e ij = top u s e r � 2 � K � i u u u u r ij − i1 i2 i3 u ik v jk iK k =1 m o v i e j v v v v j1 j2 j3 jK rij rating bottom Creato r: Y aser Abu-Mostafa - LFD Le ture 10 6/21 M � A L

Outline Sto hasti gradient des ent • Neural net w o rk mo del • Ba kp ropagation algo rithm • Creato r: Y aser Abu-Mostafa - LFD Le ture 10 7/21 M � A L

Biologi al inspiration biologi al fun tion biologi al stru ture − → 1 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 10 8/21 2 2 M � A L

Combining p er eptrons + + − − − − x 2 x 2 x 2 + + h 1 h 2 x 1 x 1 x 1 1 1 1 . 5 − 1 . 5 x 1 OR ( x 1 , x 2 ) x 1 AND ( x 1 , x 2 ) 1 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 10 9/21 1 1 x 2 x 2 M � A L

Creating la y ers 1 1 − 1 . 5 1 − 1 . 5 1 . 5 1 . 5 1 h 1 ¯ h 1 f h 2 f 1 1 − 1 − 1 ¯ 1 h 1 h 2 1 h 2 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 10 10/21 M � A L

The multila y er p er eptron 1 1 1 − 1 . 5 − 1 . 5 w 1 • x 1 . 5 1 x 1 f 1 − 1 − 1 1 x 2 1 w 2 • x 3 la y ers �feedfo rw a rd� Creato r: Y aser Abu-Mostafa - LFD Le ture 10 11/21 M � A L

A p o w erful mo del − − − − − − + + + + + + + + + + + + T a rget 8 p er eptrons 16 p er eptrons − − − − − − 2 red �ags fo r generalization and optimization Creato r: Y aser Abu-Mostafa - LFD Le ture 10 12/21 M � A L

The neural net w o rk 1 1 1 x 1 θ θ θ h ( x ) x 2 θ θ θ ( s ) s θ input x hidden la y ers 1 ≤ l < L output la y er l = L x d Creato r: Y aser Abu-Mostafa - LFD Le ture 10 13/21 M � A L

PSfrag repla ements Ho w the net w o rk op erates -4 linea r -2 0 tanh 2  4 1 ≤ l ≤ L layers   -1  w ( l ) 0 ≤ i ≤ d ( l − 1) +1 inputs -0.5 ha rd threshold ij   0 1 ≤ j ≤ d ( l ) outputs  0.5 1   d ( l − 1) − 1 � x ( l ) j = θ ( s ( l ) w ( l ) ij x ( l − 1) j ) = θ   i Apply x to x (0) i =0 θ ( s ) = tanh( s ) = e s − e − s e s + e − s 1 · · · x (0) d (0) → → x ( L ) Creato r: Y aser Abu-Mostafa - LFD Le ture 10 14/21 = h ( x ) 1 M � A L

Outline Sto hasti gradient des ent • Neural net w o rk mo del • Ba kp ropagation algo rithm • Creato r: Y aser Abu-Mostafa - LFD Le ture 10 15/21 M � A L

Applying SGD All the w eights w = { w ( l ) determine h ( x ) Erro r on example ( x n , y n ) is ij } e e ( w ) � � T o implement SGD, w e need the gradient h ( x n ) , y n = e ( w ) ∇ e ( w ) : fo r all i, j, l ∂ Creato r: Y aser Abu-Mostafa - LFD Le ture 10 16/21 ∂ w ( l ) ij M � A L

e ( w ) Computing ∂ e ( w ) W e an evaluate ∂ one b y one: analyti ally o r numeri ally ∂ w ( l ) ij top (l) x j A tri k fo r e� ient omputation: θ ∂ w ( l ) (l) ij s j e ( w ) e ( w ) (l) w × ∂ s ( l ) ij ∂ = ∂ j ∂ w ( l ) ∂ s ( l ) ∂ w ( l ) e ( w ) W e have W e only need: ∂ (l−1) ij j ij x i Creato r: Y aser Abu-Mostafa - LFD Le ture 10 17/21 ∂ s ( l ) = x ( l − 1) = δ ( l ) j bottom i j ∂ w ( l ) ∂ s ( l ) ij j M � A L

fo r the �nal la y er e ( w ) F o r the �nal la y er l = L and j = 1 : δ e ( w ) = ∂ δ ( l ) j ∂ s ( l ) j = ∂ δ ( L ) e ( w ) = ( x ( L ) 1 ∂ s ( L ) 1 − y n ) 2 1 fo r the tanh x ( L ) = θ ( s ( L ) 1 ) 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 10 18/21 θ ′ ( s ) = 1 − θ 2 ( s ) M � A L

Ba k p ropagation of δ e ( w ) top ∂ e ( w ) δ ( l − 1) (l) x j = i ∂ s ( l − 1) i δ (l) d ( l ) × ∂ s ( l ) j × ∂ x ( l − 1) ∂ � j i = ∂ s ( l ) ∂ x ( l − 1) ∂ s ( l − 1) j =1 j i i (l) w ij d ( l ) � δ ( l ) w ( l ) × θ ′ ( s ( l − 1) = × ) j ij i (l−1) x i j =1 1−( ) (l−1) 2 x i d ( l ) � Creato r: Y aser Abu-Mostafa - LFD Le ture 10 (l−1) 19/21 δ ( l − 1) = (1 − ( x ( l − 1) w ( l ) ij δ ( l ) δ i ) 2 ) i i j bottom j =1 M � A L

Ba kp ropagation algo rithm 1: Initialize all w eights w ( l ) at random top 2: fo r t = 0 , 1 , 2 , . . . do 3: Pi k n ∈ { 1 , 2 , · · · , N } ij 4: F o rw a rd: Compute all x ( l ) (l) δ j 5: Ba kw a rd: Compute all δ ( l ) 6: Up date the w eights: w ( l ) j (l) 7: Iterate to the next step until it is time to stop w ij j 8: Return the �nal w eights w ( l ) ← w ( l ) ij − η x ( l − 1) δ ( l ) (l−1) ij i j x i Creato r: Y aser Abu-Mostafa - LFD Le ture 10 20/21 ij bottom M � A L

Final rema rk: hidden la y ers lea rned nonlinea r transfo rm interp retation? 1 1 1 x 1 θ θ θ h ( x ) x 2 θ θ θ ( s ) s θ x d Creato r: Y aser Abu-Mostafa - LFD Le ture 10 21/21 M � A L