0.6 out 0.5 train r Erro v al 5 25 15 eted g E - PowerPoint PPT Presentation

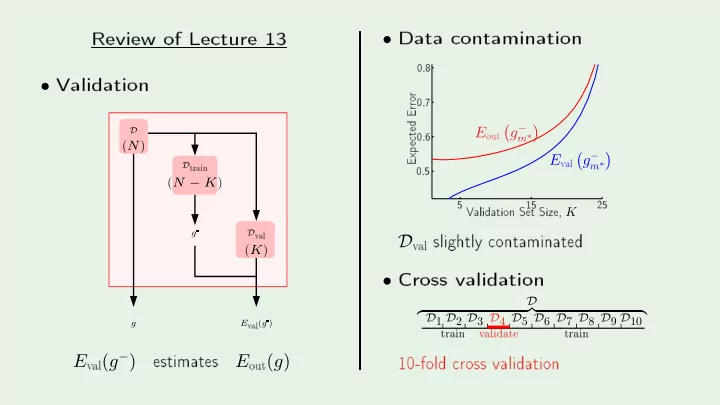
PSfrag repla ements Data ontamination Review of Le ture 13 0.8 0.7 V alidation • 0.6 out • 0.5 train r Erro v al 5 25 15 e ted g − � � E D m ∗ ( N ) Exp � g − � v al V alidation Set Size, K E m ∗ D slightly ontaminated v al ( N − K ) Cross validation train v alidate train g D D v al ( g ) ( K ) • estimates 10-fold ross validation v al ( g − ) out ( g ) D z }| { D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 g E E E

Lea rning F rom Data Y aser S. Abu-Mostafa Califo rnia Institute of T e hnology Le ture 14 : Supp o rt V e to r Ma hines Sp onso red b y Calte h's Provost O� e, E&AS Division, and IST Thursda y , Ma y 17, 2012 •

Outline Maximizing the ma rgin • The solution • Nonlinea r transfo rms • Creato r: Y aser Abu-Mostafa - LFD Le ture 14 2/20 M � A L

Better linea r sepa ration Linea rly sepa rable data Hi Hi Hi Di�erent sepa rating lines Whi h is b est? T w o questions: Hi Hi Hi 1. Why is bigger ma rgin b etter? 2. Whi h w maximizes the ma rgin? Creato r: Y aser Abu-Mostafa - LFD Le ture 14 3/20 M � A L

Rememb er the gro wth fun tion? All di hotomies with any line: Creato r: Y aser Abu-Mostafa - LFD Le ture 14 4/20 M � A L

Di hotomies with fat ma rgin F at ma rgins imply few er di hotomies infinity 0.866 0.5 0.397 infinity 0.866 0.5 0.397 Creato r: Y aser Abu-Mostafa - LFD Le ture 14 5/20 M � A L

Finding w with la rge ma rgin T x = 0 . Let x n b e the nea rest data p oint to the plane w Ho w fa r is it? 2 p relimina ry te hni alities: 1. No rmalize w : T x n | = 1 2. Pull out w 0 : | w apa rt from b T x + b = 0 The plane is no w (no x 0 ) w = ( w 1 , · · · , w d ) Creato r: Y aser Abu-Mostafa - LFD Le ture 14 6/20 w M � A L

Computing the distan e T x + b = 0 T x n + b | = 1 The distan e b et w een x n and the plane w where | w The ve to r w is ⊥ to the plane in the X spa e: T ak e x ′ and x ′′ on the plane Hi T x ′ + b = 0 T x ′′ + b = 0 x n and w T ( x ′ − x ′′ ) = 0 x’ w w x’’ = ⇒ w Hi Creato r: Y aser Abu-Mostafa - LFD Le ture 14 7/20 M � A L

and the distan e is . . . Distan e b et w een x n and the plane: T ak e any p oint x on the plane Hi x n Proje tion of x n − x on w w T ( x n − x ) distan e = x w � � � ˆ ˆ w = = ⇒ w � T x n − w T x T x n + b − w T x − b � w � Hi distan e 1 1 1 � � � � � = � = = Creato r: Y aser Abu-Mostafa - LFD Le ture 14 8/20 � w � w � w � � w � � w � M � A L

The optimization p roblem Maximize T x n + b | = 1 1 subje t to � w � T x n + b | = y n ( w T x n + b ) Noti e: | w n =1 , 2 ,...,N | w min T w Minimize 1 T x n + b ) ≥ 1 subje t to y n ( w fo r 2 w Creato r: Y aser Abu-Mostafa - LFD Le ture 14 9/20 n = 1 , 2 , . . . , N M � A L

Outline Maximizing the ma rgin • The solution • Nonlinea r transfo rms • Creato r: Y aser Abu-Mostafa - LFD Le ture 14 10/20 M � A L

Constrained optimization T w Minimize 1 T x n + b ) ≥ 1 subje t to fo r 2 w y n ( w n = 1 , 2 , . . . , N Lagrange? inequalit y onstraints = KKT w ∈ R d , b ∈ R ⇒ Creato r: Y aser Abu-Mostafa - LFD Le ture 14 11/20 M � A L

W e sa w this b efo re onst. in = Rememb er regula rization? T (Z w − y ) Minimize lin in ( w ) = E normal T w ≤ C subje t to: 1 N (Z w − y ) E w no rmal to onstraint in w in w optimize onstrain ∇ E T w t w = C Regula rization: in T w SVM: ∇ E in E w Creato r: Y aser Abu-Mostafa - LFD Le ture 14 12/20 w E w M � A L

Lagrange fo rmulation T w − T x n + b ) − 1) Minimize N L ( w , b, α ) = 1 � w.r.t. w and b and maximize w.r.t. ea h α n ≥ 0 α n ( y n ( w 2 w n =1 N � ∇ w L = w − α n y n x n = 0 n =1 N ∂ L � ∂b = − α n y n = 0 Creato r: Y aser Abu-Mostafa - LFD Le ture 14 13/20 n =1 M � A L

Substituting . . . and N N � � α n y n = 0 w = α n y n x n T w − T x n + b ) − 1 ) in the Lagrangian n =1 n =1 N L ( w , b, α ) = 1 � α n ( y n ( w 2 w T w e get n =1 N N N α n − 1 � � � L ( α ) = y n y m α n α m x n x m Maximize w.r.t. to α subje t to α n ≥ 0 fo r n = 1 , · · · , N and 2 n =1 n =1 m =1 Creato r: Y aser Abu-Mostafa - LFD Le ture 14 14/20 � N n =1 α n y n = 0 M � A L

The solution - quadrati p rogramming T x 1 T x 2 T x N T x 1 T x 2 T x N T T )   linea r y 1 y 1 x 1 y 1 y 2 x 1 . . . y 1 y N x 1 T x 1 y N y 2 x N T x 2 . . . y N y N x N T x N   1 y 2 y 1 x 2 y 2 y 2 x 2 . . . y 2 y N x 2   min α + ( − 1 quadrati o e� ients 2 α α   . . . . . . . . . . . . � �� � α   T α = 0 subje t to y N y 1 x N linea r onstraint � �� � y � �� � lo w er b ounds upp er b ounds ≤ ≤ 0 α ∞ Creato r: Y aser Abu-Mostafa - LFD Le ture 14 15/20 ���� ���� M � A L

QP hands us α onst. in = Solution: α = α 1 , · · · , α N lin E normal N � KKT ondition: F o r n = 1 , · · · , N = ⇒ w = α n y n x n w T x n + b ) − 1) = 0 n =1 in w W e sa w this b efo re! t w = C α n ( y n ( w is a supp o rt ve to r ∇ E Creato r: Y aser Abu-Mostafa - LFD Le ture 14 16/20 w α n > 0 = ⇒ x n M � A L

Supp o rt ve to rs Closest x n 's to the plane: a hieve the ma rgin T x n + b ) = 1 Hi = ⇒ y n ( w is SV � Solve w = fo r b using any SV: α n y n x n x n T x n + b ) = 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 14 17/20 y n ( w Hi M � A L

Outline Maximizing the ma rgin • The solution • Nonlinea r transfo rms • Creato r: Y aser Abu-Mostafa - LFD Le ture 14 18/20 M � A L

instead of x T z N N N α n − 1 � � � L ( α ) = y n y m α n α m z n z m 2 n =1 n =1 m =1 1 1 PSfrag repla ements PSfrag repla ements X − → Z 0 . 5 0 Creato r: Y aser Abu-Mostafa - LFD Le ture 14 19/20 0 − 1 0 0 . 5 1 − 1 0 1 M � A L

�Supp o rt ve to rs� in X spa e Supp o rt ve to rs live in Z spa e Hi In X spa e, �p re-images� of supp o rt ve to rs The ma rgin is maintained in Z spa e Generalization result E [ # of SV's ] out ] ≤ E [ E Creato r: Y aser Abu-Mostafa - LFD Le ture 14 20/20 N − 1 Hi M � A L