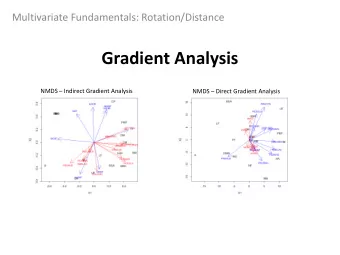
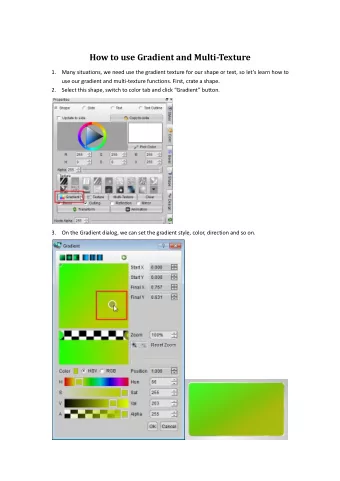
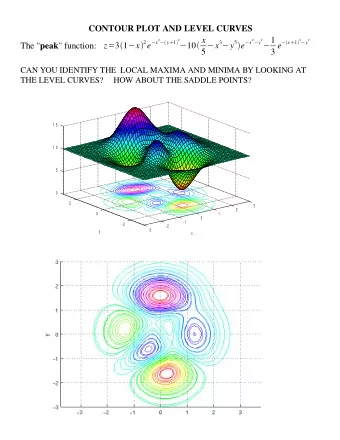
Tutorial on Gradient methods for non-convex problems Part 1 - PowerPoint PPT Presentation

Tutorial on Gradient methods for non-convex problems Part 1 Guillaume Garrigos – November 28th – ENS

What can we expect? • Does my algorithm converge? 𝑦 ∞ ≔ lim 𝑙→+∞ 𝑦 𝑙 exists? • What is the nature of the limit 𝑦 ∞ ? Global/Local minima? Saddle?

General results 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Proposition Let 0 ≪ 𝜇 𝑙 ≪ 2/𝑀 , then: 𝑔 𝑦 𝑙 is decreasing 1) 2) if 𝑦 𝑙 𝑜 → 𝑦 ∞ then 𝛼𝑔 𝑦 ∞ = 0 3) Isolated local minima are attractive [Pro 1.2.3, 1.2.5 & Ex. 1.2.18] Bertsekas, Nonlinear Programming, 1999.

General results 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Proposition Let 0 ≪ 𝜇 𝑙 ≪ 2/𝑀 , then: 𝑔 𝑦 𝑙 is decreasing 1) 2) if 𝑦 𝑙 𝑜 → 𝑦 ∞ then 𝛼𝑔 𝑦 ∞ = 0 3) Isolated local minima are attractive 𝑦 𝑙 can have no limit !! No convergence ≠ Lack of regularity, but rather wild ildness [Pro 1.2.3, 1.2.5 & Ex. 1.2.18] Bertsekas, Nonlinear Programming, 1999.

General results 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 [Ex. 3] Palis, de Melo, Geometric Theory of Dynamical Systems: An Introduction, 1982. H.B.Curry, The method of steepest descent for nonlinear minimization problems, 1944.

ሶ How to guarantee convergence? ∞ • A sufficient condition for 𝑦(𝑢) to converge is ׬ 𝑦 𝑢 𝑒𝑢 < ∞ 0

ሶ How to guarantee convergence? ∞ • A sufficient condition for 𝑦(𝑢) to converge is ׬ 𝑦 𝑢 𝑒𝑢 < ∞ 0  It is a classic result that `Finite Length ’ implies convergence  Converse is not true (but tricky): −1 𝑙 𝑦 𝑜 ≔ σ 𝑙=1 → −log(2) but σ 𝑦 𝑜+1 − 𝑦 𝑜 = σ 1 𝑜 𝑙 𝑜

ሶ How to guarantee convergence? ∞ • A sufficient condition for 𝑦(𝑢) to converge is ׬ 𝑦 𝑢 𝑒𝑢 < ∞ 0 • Length is invariant up to a reparametrization in time

ሶ How to guarantee convergence? ∞ • A sufficient condition for 𝑦(𝑢) to converge is ׬ 𝑦 𝑢 𝑒𝑢 < ∞ 0 • Length is invariant up to a reparametrization in time • We have a natural diffeomorphism 𝑔 ∘ 𝑦 ∶ [0, ∞ → 𝑡 ∞ , 𝑡 0 ] where 𝑡 0 = 𝑔(𝑦 0 ) and 𝑡 ∞ = lim ∞ 𝑔(𝑦 𝑢 )

ሶ ሶ How to guarantee convergence? ∞ • A sufficient condition for 𝑦(𝑢) to converge is ׬ 𝑦 𝑢 𝑒𝑢 < ∞ 0 • Length is invariant up to a reparametrization in time • We have a natural diffeomorphism 𝑔 ∘ 𝑦 ∶ [0, ∞ → 𝑡 ∞ , 𝑡 0 ] where 𝑡 0 = 𝑔(𝑦 0 ) and 𝑡 ∞ = lim ∞ 𝑔(𝑦 𝑢 ) 𝑔 ∘ 𝑦 −1 𝑡 • With 𝑡 = 𝑔(𝑦 𝑢 ) we can define 𝑧 𝑡 = 𝑦 s.t. −2 𝑧 𝑡 = 𝛼𝑔 𝑧 𝑡 𝛼𝑔 𝑧 𝑡

ሶ ሶ How to guarantee convergence? ∞ • A sufficient condition for 𝑦(𝑢) to converge is ׬ 𝑦 𝑢 𝑒𝑢 < ∞ 0 • Length is invariant up to a reparametrization in time • We have a natural diffeomorphism 𝑔 ∘ 𝑦 ∶ [0, ∞ → 𝑡 ∞ , 𝑡 0 ] where 𝑡 0 = 𝑔(𝑦 0 ) and 𝑡 ∞ = lim ∞ 𝑔(𝑦 𝑢 ) 𝑔 ∘ 𝑦 −1 𝑡 • With 𝑡 = 𝑔(𝑦 𝑢 ) we can define 𝑧 𝑡 = 𝑦 s.t. −2 𝑧 𝑡 = 𝛼𝑔 𝑧 𝑡 𝛼𝑔 𝑧 𝑡 𝑡 0 1 • So the length becomes ׬ ‖ 𝑒𝑡 𝑡 ∞ ‖𝛼𝑔 𝑧 𝑡 Finite interval ! Ignore 𝛼𝑔 𝑧 𝑡 = 0

ሶ How to guarantee convergence? ∞ 𝑡 0 1 • How to upper bound ׬ 𝑦 𝑢 𝑒𝑢 = ׬ ‖ 𝑒𝑡 ? 0 𝑡 ∞ ‖𝛼𝑔 𝑧 𝑡

ሶ How to guarantee convergence? ∞ 𝑡 0 1 • How to upper bound ׬ 𝑦 𝑢 𝑒𝑢 = ׬ ‖ 𝑒𝑡 ? 0 𝑡 ∞ ‖𝛼𝑔 𝑧 𝑡 • ``Naive ’’ hypothesis: 𝛼𝑔 𝑧 ≥ 𝐷 i.e. sharpness

ሶ How to guarantee convergence? ∞ 𝑡 0 1 • How to upper bound ׬ 𝑦 𝑢 𝑒𝑢 = ׬ ‖ 𝑒𝑡 ? 0 𝑡 ∞ ‖𝛼𝑔 𝑧 𝑡 • ``Naive ’’ hypothesis: 𝛼𝑔 𝑧 ≥ 𝐷 i.e. sharpness

ሶ How to guarantee convergence? ∞ 𝑡 0 1 • How to upper bound ׬ 𝑦 𝑢 𝑒𝑢 = ׬ ‖ 𝑒𝑡 ? 0 𝑡 ∞ ‖𝛼𝑔 𝑧 𝑡 • ``Naive ’’ hypothesis: 𝛼𝑔 𝑧 ≥ 𝐷 i.e. sharpness 1 • ``Smart’’ hypothesis: ‖ ≤ 𝜒′(𝑡) with 𝜒 ≥ 0, 𝜒 ↑ ‖𝛼𝑔 𝑧 𝑡 so the length is ≤ 𝜒 𝑡 0 − 𝜒 𝑡 ∞ ≤ 𝜒(𝑡 0 )

ሶ How to guarantee convergence? ∞ 𝑡 0 1 • How to upper bound ׬ 𝑦 𝑢 𝑒𝑢 = ׬ ‖ 𝑒𝑡 ? 0 𝑡 ∞ ‖𝛼𝑔 𝑧 𝑡 • ``Naive ’’ hypothesis: 𝛼𝑔 𝑧 ≥ 𝐷 i.e. sharpness 1 • ``Smart’’ hypothesis: ‖ ≤ 𝜒′(𝑡) with 𝜒 ≥ 0, 𝜒 ↑ ‖𝛼𝑔 𝑧 𝑡 so the length is ≤ 𝜒 𝑡 0 − 𝜒 𝑡 ∞ ≤ 𝜒(𝑡 0 ) • In other words 𝜒 ′ 𝑔 𝑦 𝑢 𝛼𝑔 𝑦 𝑢 ≥ 1 i.e. 𝜒 ∘ 𝑔 is sharp: 𝛼 𝜒 ∘ 𝑔 𝑦 ≥ 1

The Łojasiewicz property Definition We say that 𝑔 is Łojasiewicz at a critical point 𝑦 ∗ if 𝜒 ′ 𝑔 𝑦 − 𝑔 𝑦 ∗ 𝛼𝑔 𝑦 ≥ 1, • with 𝜒: [0, ∞[→ [0, ∞[ s.t. 𝜒 0 = 0 , 𝜒 ↑ , 𝜒 concave 𝑦 ′ ∈ 𝔺 𝑦 ∗ , 𝜀 𝑔 𝑦 ∗ < 𝑔 𝑦′ < 𝑔 𝑦 ∗ + 𝑠 } • for all 𝑦 ∈ Definition • 𝑔 is Łojasiewicz if it is Łojasiewicz at every critical point • 𝑔 is p- Łojasiewicz if it is Łojasiewicz at every critical point with 𝜒 𝑡 ≃ 𝑡 1/𝑞 : 𝜈(𝑔 𝑦 − 𝑔 𝑦 ∗ ) 𝑞−1 ≤ 𝑞 𝛼𝑔 𝑦

The Łojasiewicz property : convergence 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Theorem (convergence) Let 𝑔 be Łojasiewicz and 𝜇 𝑙 ∈ ]0,2/𝑀[ . If 𝑦 𝑙 is bounded , then it converges to some critical point 𝑦 ∞ . Theorem (capture) Let 𝑔 be Łojasiewicz and 𝜇 𝑙 ∈ ]0,2/𝑀[ . For every 𝑦 ∗ ∈ 𝑏𝑠𝑕𝑛𝑗𝑜 𝑔 , if 𝑦 0 ∼ 𝑦 ∗ then 𝑦 𝑙 converges to 𝑦 ∞ ∈ 𝑏𝑠𝑕𝑛𝑗𝑜 𝑔 . Łojasiewicz. Sur les trajectoires du gradient d’une fonction analytique, 1984 . Absil, Mahony, Andrews. Convergence of the Iterates of Descent Methods for Analytic Cost Functions, 2005.

The Łojasiewicz property : convergence 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Sketch of proof : show that 𝜒 ′ 𝑡 ≥ ‖ ሶ 𝑦 𝑢 ‖

The Łojasiewicz property : convergence 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Sketch of proof : show that 𝜒 ′ 𝑡 ≥ ‖ ሶ 𝑦 𝑢 ‖ 𝜒 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ − 𝜒 𝑔 𝑦 𝑙+1 ) − 𝑔(𝑦 ∗ )

The Łojasiewicz property : convergence 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Sketch of proof : show that 𝜒 ′ 𝑡 ≥ ‖ ሶ 𝑦 𝑢 ‖ 𝜒 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ − 𝜒 𝑔 𝑦 𝑙+1 ) − 𝑔(𝑦 ∗ ) ≥ 𝜒′(𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ )(𝑔 𝑦 𝑙 − 𝑔 𝑦 𝑙+1 ) because 𝜒 concave

The Łojasiewicz property : convergence 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Sketch of proof : show that 𝜒 ′ 𝑡 ≥ ‖ ሶ 𝑦 𝑢 ‖ 𝜒 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ − 𝜒 𝑔 𝑦 𝑙+1 ) − 𝑔(𝑦 ∗ ) ≥ 𝜒′(𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ )(𝑔 𝑦 𝑙 − 𝑔 𝑦 𝑙+1 ) because 𝜒 concave 2 ≥ 𝜒 ′ 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ 𝑦 𝑙+1 − 𝑦 𝑙 𝑑 𝜇,𝑀 with Descent Lemma

The Łojasiewicz property : convergence 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Sketch of proof : show that 𝜒 ′ 𝑡 ≥ ‖ ሶ 𝑦 𝑢 ‖ 𝜒 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ − 𝜒 𝑔 𝑦 𝑙+1 ) − 𝑔(𝑦 ∗ ) ≥ 𝜒′(𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ )(𝑔 𝑦 𝑙 − 𝑔 𝑦 𝑙+1 ) because 𝜒 concave 2 ≥ 𝜒 ′ 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ 𝑦 𝑙+1 − 𝑦 𝑙 𝑑 𝜇,𝑀 with Descent Lemma = 𝜒 ′ 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ 𝐷 𝜇,𝑀 𝑦 𝑙+1 − 𝑦 𝑙 𝛼𝑔 𝑦 𝑙

The Łojasiewicz property : convergence 𝑦 𝑙+1 = 𝑦 𝑙 − 𝜇 𝑙 𝛼𝑔 𝑦 𝑙 f ∶ R n → R is of class C 𝑀 1,1 Sketch of proof : show that 𝜒 ′ 𝑡 ≥ ‖ ሶ 𝑦 𝑢 ‖ 𝜒 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ − 𝜒 𝑔 𝑦 𝑙+1 ) − 𝑔(𝑦 ∗ ) ≥ 𝜒′(𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ )(𝑔 𝑦 𝑙 − 𝑔 𝑦 𝑙+1 ) because 𝜒 concave 2 ≥ 𝜒 ′ 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ 𝑦 𝑙+1 − 𝑦 𝑙 𝑑 𝜇,𝑀 with Descent Lemma = 𝜒 ′ 𝑔 𝑦 𝑙 − 𝑔 𝑦 ∗ 𝐷 𝜇,𝑀 𝑦 𝑙+1 − 𝑦 𝑙 𝛼𝑔 𝑦 𝑙