UPPAAL Tutorial UPPAAL Tutorial UPPAAL Tutorial Introduction Introduction Alexandre David Paul Pettersson RTSS’05 Collaborators @UPPsala @AALborg � Wang Yi � Kim G Larsen � Paul Pettersson � Gerd Behrman � John Håkansson � Arne Skou � Anders Hessel � Brian Nielsen � Pavel Krcal � Alexandre David � Leonid Mokrushin � Jacob Illum Rasmussen � Shi Xiaochun � Marius Mikucionis @Elsewhere Emmanuel Fleury, Didier Lime, Johan Bengtsson, Fredrik Larsson, Kåre J � Kristoffersen, Tobias Amnell, Thomas Hune, Oliver Möller, Elena Fersman, Carsten Weise, David Griffioen, Ansgar Fehnker, Frits Vandraager, Theo Ruys, Pedro D’Argenio, J-P Katoen, Jan Tretmans, Judi Romijn, Ed Brinksma, Martijn Hendriks, Klaus Havelund, Franck Cassez, Magnus Lindahl, Francois Laroussinie, Patricia Bouyer, Augusto Burgueno, H. Bowmann, D. Latella, M. Massink, G. Faconti, Kristina Lundqvist, Lars Asplund, Justin Pearson... 1
Real-Time Systems sensors Task Task Task Task actuators Controller Program Plant Discrete Continuous Real-Time System Real-Time System A system where correctness not only depends on the A system where correctness not only depends on the logical order of events but also on their timing !! logical order of events but also on their timing !! E.g.: Air Bags, Cruise Control, ABS Process Control, Production Lines, Robots Real-time Protocols DVD/CD Players Real-Time Model-Checking Plant Controller Program Continuous Discrete sensors Task Task Task Task actuators 1 2 a 1 2 Model of 3 4 tasks b c 3 4 1 (automatic?) 2 a Model of 1 2 a environment b c 3 4 (user-supplied) b c 3 4 UPPAAL Model 2
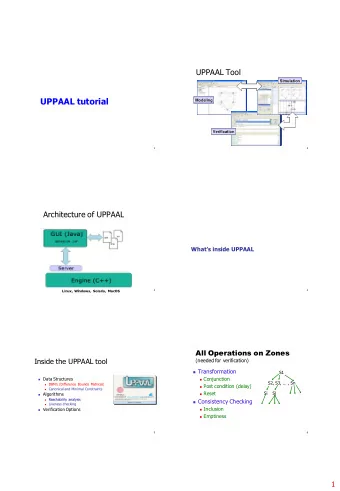
Model-Checking Model: A Yes! UPPAAL No! Requirement Diagnostic A ² F Specification: F Information A – Model: Network of Timed Automata F – Requirement: temporal logical formula, e.g. � Invariant: something bad will never happen, something may happen � Liveness: something will eventually happen UPPAAL Tool Simulation Modeling Verification 3
UPPAAL’s Architecture Linux, W indow s, Solaris, MacOS Outline Tutorial Day � Session 1: Introduction � Session 3: Inside UPPAAL (9:00-10:30) Advanced (13:30-15:00) Lecture Lecture � � • Tool presentation • Virtual machine • Modeling: Timed Automata w. • Sharing extensions • Optimizations • Query Language • Simulation • Symbolic Semantics • Modeling Patterns Demo/Exercise � Session 4: Beyond UPPAAL � � Session 2: Inside UPPAAL Basics (15:30-17:00) (11:00-12:00) Lecture � Lecture � • UPPAAL Cora • Reachability Analysis • UPPAAL Tron • Difference Bounded Matrices • UPPAAL TIGA • Liveness checking • CoVer • Times � Lunch Break • Open source modules Exercise � 4
Modeling Formalisms � Timed Automata � Query Language � Symbolic Semantics Timed Automata: Light Control press? press? press? Off Light Bright press? WANT: • pressed once = light • pressed twice quickly = light will get brighter • pressed again = light off. 5
Timed Automata: Light Control with Timing press? X:= 0 press? press? Off Light Bright X< = 3 press? X> 3 SOLUTI ON: Add real-valued clock x to measure the delay between press events Alur & Dill 1990 Timed Automata review Action Clocks: x, y used for synchronization n Guard Boolean combination of integer bounds on clocks Reset x< = 5 & y> 3 Action performed on clocks State a where v,u are in R ( location , x = v , y = u ) Transitions x := 0 a Discrete Trans ( n , x = 2.4 , y = 3.1415 ) m ( m , x = 0 , y = 3.1415 ) e(1.1) Delay Trans ( n , x = 2.4 , y = 3.1415 ) ( n , x = 3.5 , y = 4.2415 ) 6
Timed Automata review Invariants n Clocks: x, y x< = 5 Transitions x< = 5 & y> 3 e(3.2) Location ( n , x = 2.4 , y = 3.1415 ) Invariants a e(1.1) ( n , x = 2.4 , y = 3.1415 ) ( n , x = 3.5 , y = 4.2415 ) x := 0 m y< = 10 I nvariants I nvariants g4 ensure g1 ensure g2 g3 progress!! progress!! Timed Automata: Example guard location a a action reset-set 7
Timed Automata: Example guard location a a a a action reset-set Timed Automata: Example ≤ a 3 x Invariant 8
Timed Automata: Example a a a ≤ 3 a x Invariant Networks of Timed Automata with (finite) integer variables m1 l1 x> = 2 y< = 4 Two-way synchronization i= = 3 …………. Two-way synchronization on complementary actions. on complementary actions. a! a? x := 0 Closed Systems! Closed Systems! i:= i+ 4 l2 m2 Example transitions tau ( l1 , m1 ,………, x= 2, y= 3.5, i= 3,…..) ( l2,m2 ,……..,x= 0, y= 3.5, i= 7,…..) 9
Train Crossing [WPD-FORTE’94] Stopable Area [10,20] [3,5] Crossing [7,15] River Queue Gate Train Crossing Communication via channels and shared variable. Stopable Area [10,20] appr, [3,5] leave stop Crossing [7,15] e e go River empty Queue nonempty hd, add,rem Gate 10
Scheduling with UPPAAL night 5 10 20 25 damaged bride (max 2 men) with mines lamp Safe Side Unsafe Side I f possible find schedule for all four m en to reach safe side in 6 0 m in. Bridge Problem UNSAFE SAFE Mines 5 10 25 20 � Can be modeled and solved with timed automata in UPPAAL. 11
Timed Automata in U PPAAL � Timed Automata with Invariants � urgent action channels, � urgent and committed locations, � data-variables (with bounded domains), � arrays of data-variables, � constants, � guards and assignments over data-variables and arrays…, � templates with local clocks, data-variables, and constants. � C subset Declarations in UPPAAL � The syntax used for declarations in UPPAAL is similar to the syntax used in the C programming language. � Clocks : � Syntax: � clock x1, …, xn ; � Example: Declares two clocks: x and y. � clock x, y; 12
Declarations in UPPAAL (cont.) � Data variables � Syntax: Integer with “default” domain. � int n1, … ; Integer with domain “l” to “u”. � int[l,u] n1, … ; Integer array w. elements n1[0] to � int n1[m], … ; n1[m-1]. � Example; � int a, b; � int[0,1] a, b[5][6]; Declarations in UPPAAL (cont.) � Actions (or channels): � Syntax: Ordinary channels. � chan a, … ; Urgent actions (see later) � urgent chan b, … ; � Example: � chan a, b; � urgent chan c; 13
Declarations U PPAAL (const.) � Constants � Syntax: � const int c1 = n1; � Example: � const int[0,1] YES = 1; � const bool NO = false; Timed Automata in U PPAAL Location Invariants Clock Assignments = < <= x = n inv :: x n | x n | inv , inv n x< = 5 Variable Assignments clock natural number “and” = : i Expr x> = 5 && y> 3 = :: | [ ] | Expr i i Expr = :: | | , g g g g g c d − | | n Expr a! = ⊗ ⊗ + :: | g x n x y n + c Clock guards | Expr Expr x = 0 = :: g Expr op Expr − Data guards d | Expr Expr m ⊗ ∈ < <= == >= > { , , , , } * | Expr Expr y< = 10 g4 ∈ < <= == >= > = / | op { , , , , , ! } Expr Expr g1 g2 g3 ( ? : ) g Expr Expr d 14
Timed Automata in U PPAAL Location Invariants Clock Assignments x = = < <= : n :: | | , inv x n x n inv inv n x< = 5 Variable Assignments Actions: clock natural number “and” = i : Expr x> = 5 , y> 3 • “a” name of action = :: | [ ] | Expr i i Expr = • a! or a? :: | | , g g g g g c d − n | Expr | a! • one or zero per edge = ⊗ ⊗ + :: | g x n x y n + c Clock guards | Expr Expr x := 0 = :: g Expr op Expr − Data guards d Expr Expr | m ⊗ ∈ < <= == >= > { , , , , } * | Expr Expr y< = 10 g4 ∈ < <= == >= > = { , , , , , ! } Expr / Expr | op g1 g2 g3 ( ? : ) g Expr Expr d Broadcast Synchronization � Declared like broadcast chan a, b, c[2]; � If a is a broadcast channel: � a! = Emmision of broadcast � a? = Reception of broadcast � A set of edges in different processes can synchronize if one is emitting and the others are receiving on the same b.c. channel. � A process can always emit. � Receivers must synchronize if they can. � No blocking. 15
Urgent Channels: Example 1 � Suppose the two edges in P: Q: automata P and Q should be l 1 s 1 taken as soon as possible. � I.e. as soon as both automata a! a? are ready (simultaneously in locations l 1 and s 1 ). � How to model with invariants l 2 s 2 if either one may reach l 1 or s 1 first? Urgent Channels: Example 1 � Suppose the two edges in P: Q: automata P and Q should be l 1 s 1 taken as soon as possible � I.e. as soon as both automata a! a? are ready (simultaneously in locations l 1 and s 1 ). � How to model with invariants l 2 s 2 if either one may reach l 1 or s 1 first? � Solution : declare action “a” as urgent. 16
Urgent Channels urgent chan hurry; Informal Semantics: • There will be no delay if transition with urgent action can be taken. Restrictions: • No clock guard allowed on transitions with urgent actions. • Invariants and data-variable guards are allowed. Urgent Channel: Example 2 � Assume i is a data variable. P: � We want P to take the transition l 1 from l1 to l2 as soon as i==5. i==5 l 2 17
Recommend
More recommend
