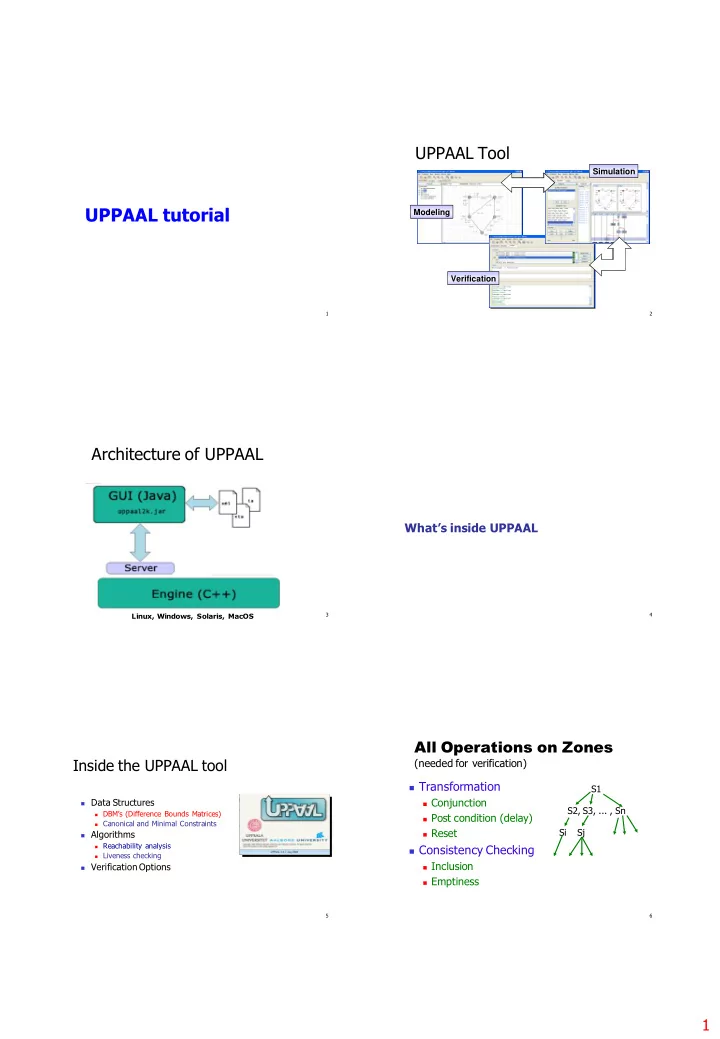

UPPAAL Tool Simulation UPPAAL tutorial Modeling Verification 1 2 Architecture of UPPAAL What’s inside UPPAAL Linux, Windows, Solaris, MacOS 3 4 All Operations on Zones Inside the UPPAAL tool (needed for verification) Transformation S1 Conjunction Data Structures S2, S3, ... , Sn DBM’s (Difference Bounds Matrices) Post condition (delay) Canonical and Minimal Constraints Reset Si Sj Algorithms Reachability analysis Consistency Checking Liveness checking Inclusion Verification Options Emptiness 5 6 1
Datastructures for Zones in UPPAAL Zones = Conjuctive constraints -4 Difference Bounded Matrices A zone Z is a conjunctive formula: x1 x2 [Bellman58, Dill89] 4 g 1 & g 2 & ... & g n 3 3 -2 2 -2 Minimal Constraint Form 2 where g i may be x i ~ b i or x i -x j ~b ij x0 x3 [RTSS97] 1 Use a zero-clock x 0 (constant 0), we have 5 {x i -x j ~ b ij | ~ is < or , i,j n} Clock Difference Diagrams [CAV99] This can be represented as a MATRIX, DBM (Difference Bound Matrices) 7 8 Canonical Dastructures for Zones Canonical Datastructures for Zones Bellman 1958, Dill 1989 Difference Bounded Matrices Difference Bounded Matrices Bellman 1958, Dill 1989 Inclusion Inclusion x x x 1 2 1 2 x<=1 x<=1 1 2 Shortest y-x<=2 y-x<=2 Z1 Z1 Path 3 Graph y Graph y 0 0 y 0 z-y<=2 z-y<=2 Closure 9 9 5 z<=9 2 z<=9 2 z z 2 z Z1 Z2 ! ? ? ? ? Z2 Z2 x x<=2 x x<=2 x 2 3 Shortest 2 3 2 3 y-x<=3 y-x<=3 Path 3 3 3 y<=3 Graph y<=3 Graph 0 y y y 0 0 Closure z-y<=3 z-y<=3 6 3 7 7 3 3 z z<=7 z<=7 z z 9 10 Canonical Datastructures for Zones Canonical Datastructures for Zones Difference Bounded Matrices Bellman 1958, Dill 1989 Difference Bounded Matrices Conjunction Emptiness y y Z g Z x 1<=x, 1<=y x x 1<=x, 1<=y -2<=x-y<=3 1 Z x<=1 -2<=x-y<=3 3<=x 3 y>=5 Graph 0 y-x<=3 y x -5 x -3 -3 x Add new edge -1 -1 3 for g 3 0 0 3 0 Negative Cycle 2 iff 2 2 -1 y -1 y -1 y empty solution set 11 12 2
Canonical Dastructures for Zones Canonical Datastructures for Zones Difference Bounded Matrices Difference Bounded Matrices y Reset y Delay y y {y}Z Z x x Z Z 1<=x, 1<=y x x -2<=x-y<=3 y=0, 1<=x 1<= x <=4 1<=x, 1<=y 1<= y <=3 -2<=x-y<=3 x Remove all -1 -1 bounds x 3 4 4 x x 0 0 involving y 0 Remove -1 Shortest and set y to 0 -1 -1 2 upper 0 3 3 Path 0 0 -1 y 3 3 0 y bounds Closure on clocks 2 2 -1 y -1 y -1 y 13 14 Datastructures for Zones in UPPAAL COMPLEXITY -4 Computing the shortest path closure, the Difference Bounded Matrices x1 x2 [Bellman58, Dill89] 4 cannonical form of a zone: O(n 3 ) [Dijkstra’s alg.] 3 3 -2 2 -2 Run-time complexity, mostly in O(n) 2 Minimal Constraint Form x0 x3 [RTSS97] 1 (when we keep all zones in cannonical form) 5 Clock Difference Diagrams [CAV99] 15 16 Graph Reduction Algorithm Minimal Graph -4 G: weighted graph -4 x1 x1 x2 x2 1. Equivalence classes based Shortest x1-x2<=-4 -1 Path on 0-cycles. x2-x1<=10 10 4 Closure x3-x1<=2 3 2 3 3 -2 O(n 3 ) 2 x2-x3<=2 -2 2 2 x0-x1<=3 7 x3-x0<=5 x3 x0 x0 x3 5 1 5 -4 (DBM) x2 Shortest x1 Path Space worst O(n 2 ) Reduction practice O(n) O(n 3 ) 2 3 3 2 (Minimal graph, a.ka. compact data structure) x0 x3 17 18 3
Graph Reduction Algorithm Graph Reduction Algorithm G: weighted graph G: weighted graph 1. Equivalence classes based 1. Equivalence classes based on 0-cycles. on 0-cycles. 2. Graph based on 2. Graph based on representatives. representatives. Safe to remove redundant edges Safe to remove redundant edges 3. Shortest Path Reduction = One cycle pr. class + Removal of redundant edges between classes 19 20 Datastructures for Zones in UPPAAL Other Symbolic Datastructures -4 CDD-representations NDD’s Maler et. al. Difference Bounded Matrices x1 x2 [Bellman58, Dill89] 4 CDD’s UPPAAL/CAV99 3 3 -2 2 DDD’s Møller, Lichtenberg -2 2 Minimal Constraint Form Polyhedra HyTech x0 x3 [RTSS97] 1 5 ...... Clock Difference Diagrams [CAV99] 21 22 Timed CTL in UPPAAL Inside the UPPAAL tool E<> p | A[] p | E[] p | A<> p | p - -> q Data Structures P ::= A.l | g c | g d | not p| p or p | p and p | p imply p DBM’s (Difference Bounds Matrices) Canonical and Minimal Constraints Algorithms Reachability analysis Process predicate Clock Liveness checking Location over data variables constraint Verification Options (a location in automaton A) denotes A[] (p imply A<> q) SAFETY PROPERTIES 23 24 4
Timed CTL (a simplified version) We have a search problem Syntax Symbolic state (n 0 ,Z 0 ) :: = p | | | EX | E[ U ] | A[ U ] Symbolic transitions where p AP (atomic propositions) or Clock constraint S2, S3 ...... Sn Derived Operators T1 T2 AG p EF p Reachable? p p E<> A[] P in UPPAAL E<> P in UPPAAL 26 25 Forward Reachability Forward Reachability Init -> Final ? Init -> Final ? INITIAL Passed := Ø; INITIAL Passed := Ø; Waiting := {(n0,Z0)} Waiting := {(n0,Z0)} Final Final Waiting Waiting REPEAT REPEAT n,Z - pick (n,Z) in Waiting - pick (n,Z) in Waiting - if for some Z’ Z - if for some Z’ Z (n,Z’) in Passed then STOP (n,Z’) in Passed then STOP - else /explore/ add - else (explore) add { (m,U) : (n,Z) => (m,U) } { (m,U) : (n,Z) => (m,U) } to Waiting ; to Waiting ; Add (n,Z) to Passed Add (n,Z) to Passed n,Z’ UNTIL Waiting = Ø UNTIL Waiting = Ø Init Init Passed Passed or or Final is in Waiting Final is in Waiting 27 28 Forward Reachability Forward Reachability Init -> Final ? Init -> Final ? INITIAL Passed := Ø; INITIAL Passed := Ø; Waiting := {(n0,Z0)} Waiting := {(n0,Z0)} Waiting Final Waiting Final m,U m,U REPEAT REPEAT - pick (n,Z) in Waiting - pick (n,Z) in Waiting n,Z n,Z - if for some Z’ Z - if for some Z’ Z (n,Z’) in Passed then STOP (n,Z’) in Passed then STOP - else /explore/ add - else /explore/ add { (m,U) : (n,Z) => (m,U) } { (m,U) : (n,Z) => (m,U) } to Waiting ; to Waiting ; Add (n,Z) to Passed Add (n,Z) to Passed n,Z’ n,Z’ UNTIL Waiting = Ø UNTIL Waiting = Ø Init Init Passed Passed or or Final is in Waiting Final is in Waiting 29 30 5
Forward Reachability Init -> Final ? Further question INITIAL Passed := Ø; Waiting := {(n0,Z0)} Waiting Final m,U REPEAT Can we find the path with shortest delay, leading to P ? - pick (n,Z) in Waiting n,Z (i.e. a state satisfying P) - if for some Z’ Z (n,Z’) in Passed then STOP - else /explore/ add { (m,U) : (n,Z) => (m,U) } OBSERVATION: to Waiting ; Many scheduling problems can be phrased naturally as Add (n,Z) to Passed n,Z’ reachability problems for timed automata. UNTIL Waiting = Ø Init Passed or Final is in Waiting 31 32 Verification vs. Optimization State reachable? Verification Algorithms: OPTIMAL REACHABILITY Checks a logical property of the entire state-space of a model. 80 Efficient Blind search. Optimization Algorithms: The maximal and minimal delay problem Min time of reaching state? Finds (near) optimal solutions. Uses techniques to avoid non- optimal parts of the state-space (e.g. Branch and Bound). Goal: solve opt. problems with 60 verification. 33 34 Find the trace leading to P with min delay Find the trace leading to P with min delay S 0 S 0 There may Idea: delay as ” Cost ” to reach p be a lot of p a state, thus cost increases with time at rate 1 pathes leading p to P p p p p p p p p p Which one p p with the shortest p p p p p p delay? p p pp p p p p pp p p p p p p 35 36 6
Recommend
More recommend