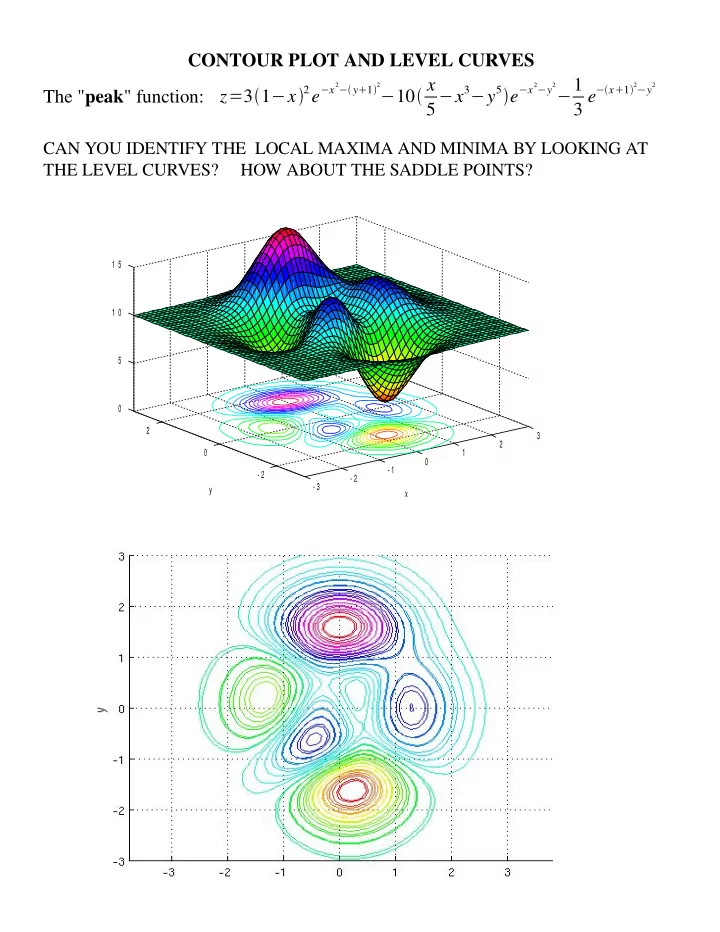
CONTOUR PLOT AND LEVEL CURVES 1 2 y 1 2 10 x 2 y 2 2 y 2 - - PDF document

CONTOUR PLOT AND LEVEL CURVES The "peak" function: z=31−x2e−x

2− y1 2

−10 x 5 −x3−y5e−x

2−y 2

−1 3 e−x1

2−y 2

CAN YOU IDENTIFY THE LOCAL MAXIMA AND MINIMA BY LOOKING AT THE LEVEL CURVES? HOW ABOUT THE SADDLE POINTS?

• 3
• 2
• 1

1 2 3

• 2

2 5 1 0 1 5 x y

Answer:

x≈1.28 , y≈−0.0048 Local Maximum x≈.228 , y≈−1.625 Local minimum x≈−.460 , y≈−.629 Local Maximum x≈−1.35 , y≈.204 Local minimum x≈−0.01 , y≈1.58 Local Maximum x≈.296 , y≈.320 Local minimum x≈−.266 , y≈.467 Saddle point x≈.416 , y≈−.394 Saddle point x≈1.10 , y≈.854 Saddle point Below, "m" stands for local minimum, "M" stands for local maximum and "S" stands for Saddle point.