S 3 identified by a rep. identified by a rep. n n = # of = # - PDF document

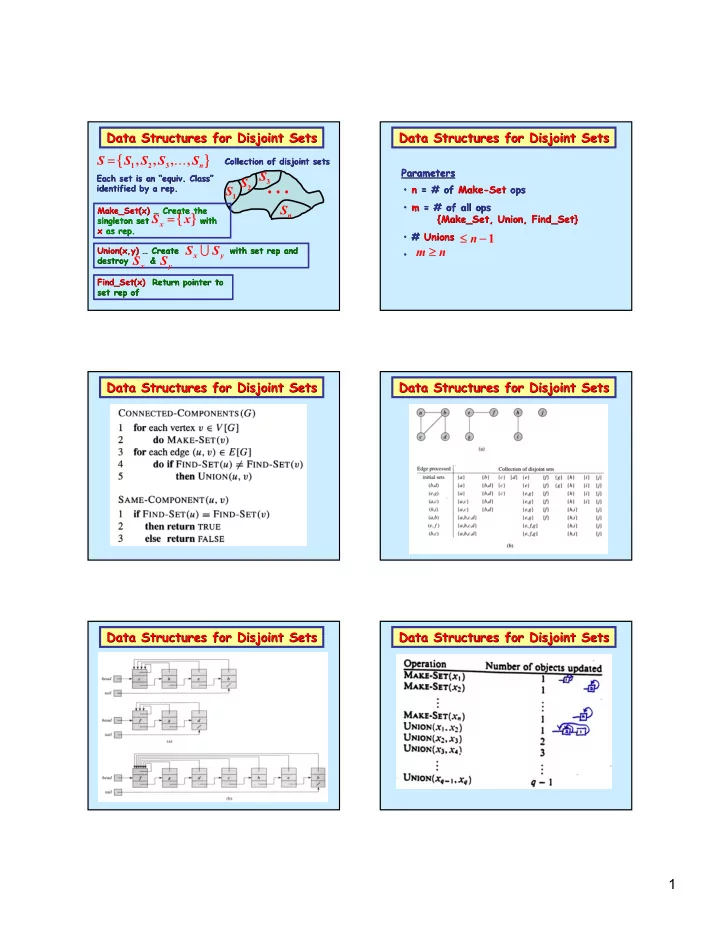
Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets { } = … Collection of disjoint sets Collection of disjoint sets S S S , , S , , S 1 2 3 n Parameters Parameters Each set is an “ Each set is an “equiv. Class equiv. Class” ” S � S 3 identified by a rep. identified by a rep. • n n = # of = # of Make Make- -Set Set ops ops • 2 S 1 • m m = # of all ops = # of all ops • Make_Set(x) Make_Set(x ) … … Create the Create the S { } = {Make_Set Make_Set, Union, , Union, Find_Set Find_Set} } n { singleton set with singleton set with S x x x x as rep. as rep. • # # Unions Unions • ≤ ≤ − − n 1 ∪ ≥ Union(x,y Union(x,y) ) … … Create with set rep and Create with set rep and S S • m • n x y destroy & destroy & S S x y Find_Set(x) Find_Set(x ) Return pointer to Return pointer to set rep of set rep of Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets 1

Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets Data Structures for Disjoint Sets − − n 1 ( n 1) n ∑ + + + + + + + − = = = … 2 1 2 3 ( n 1) j O n ( ) 2 = j 1 Weighted- Weighted -Union Heuristic Union Heuristic Disjoint- Disjoint -Set Forest Representation Set Forest Representation • • Each rep has a Each rep has a Length Length- -of of- -List List field field • Use this to append smaller sets to larger Use this to append smaller sets to larger • ones ones Theorem Theorem. If the . If the Linked Linked- -List representation List representation of sets and if the of sets and if the weighted weighted- -union heuristic union heuristic are used, and if a sequence of m are used, and if a sequence of m { {Make_Set Make_Set, Union, , Union, Find_Set Find_Set} ops are used } ops are used (with n (with n Make Make- -Set ops Set ops), then the ), then the computational time taken is computational time taken is Union Union ( ( ) ) + O m n lg n A Problem A Problem Data Structures for Disjoint Sets Data Structures for Disjoint Sets 2

Heuristics to Improve Running Time Heuristics to Improve Running Time Data Structures for Disjoint Sets Data Structures for Disjoint Sets • Union by Rank Union by Rank • • Path Compression • Path Compression Each node has a field containing Each node has a field containing Rank Rank, which , which is an upper bound on the height of the node is an upper bound on the height of the node 3