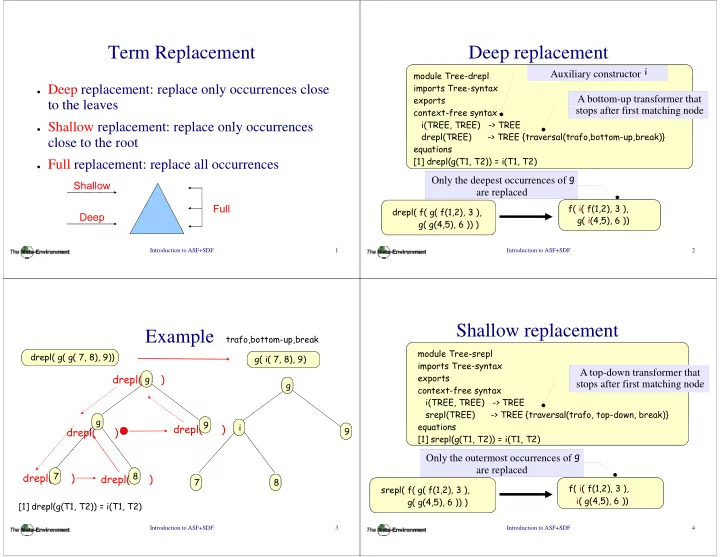
Term Rep placement Deep rep lacement Auxiliary constructor i Auxiliary constructor i module Tree-drepl d l T d l imports Tree-syntax ● Deep replacement: repla ace only occurrences close exports A bottom-up transformer that to the leaves to the leaves context-free syntax stops after first matching node f fi hi d i(TREE, TREE) -> TREE ● Shallow replacement: re eplace only occurrences drepl(TREE) -> TREE {tra drepl(TREE) TREE {tra versal(trafo bottom-up break)} versal(trafo,bottom up,break)} close to the root l t th t equations [1] drepl(g(T1, T2)) = i(T1, T2) ● Full replacement: replac ce all occurrences nces of g Only the deepest occurren Shallow are replaced f( i( f(1,2), 3 ), Full drepl( f( g( f(1,2), 3 ), Deep g( i(4,5), 6 )) g( g(4,5), 6 )) ) Introduction to ASF+SDF 1 Introduction to ASF+SDF 2 Shallow re eplacement Exam mple trafo,bottom-up,break module Tree-srepl d l T l drepl( g( g( 7, 8), 9)) g( i( 7, 8), 9) imports Tree-syntax A top-down transformer that drepl( ) p ( ) exports g g g g stops after first matching node stops after first matching node context-free syntax i(TREE, TREE) -> TREE srepl(TREE) TREE {tra srepl(TREE) -> TREE {tra aversal(trafo top-down break)} aversal(trafo, top down, break)} g 9 equations dr repl( ) i drepl( ) 9 [1] srepl(g(T1, T2)) = i(T1, T2) ) ences of g Only the outermost occurre are replaced 7 8 drepl( ) p ( ) drepl( ) drepl( ) 7 7 8 8 f( i( f(1,2), 3 ), srepl( f( g( f(1,2), 3 ), i( g(4,5), 6 )) g( g(4,5), 6 )) ) [1] drepl(g(T1, T2)) = i(T1, T2) Introduction to ASF+SDF 3 Introduction to ASF+SDF 4
Full repl lacement Exam mple trafo, top-down, break module Tree-frepl d l T f l srepl( g( g( 7, 8), 9)) i( g( 7, 8), 9) imports Tree-syntax A top-down transformer that srepl( ) p ( ) exports g g i i continues after each matching node continues after each matching node context-free syntax i(TREE, TREE) -> TREE frepl(TREE) -> TREE {tra frepl(TREE) TREE {tra aversal(trafo,top down,continue)} aversal(trafo top-down continue)} g 9 equations g 9 top-down and [1] frepl(g(T1, T2)) = i(T1, T2) ) bottom up have bottom-up have g are re here the same effect All occurrences of eplaced 7 8 7 7 8 8 f( i( f(1,2), 3 ), frepl( f( g( f(1,2), 3 ), i( i(4,5), 6 )) g( g(4,5), 6 )) ) [1] srepl(g(T1, T2)) = i(T1, T2) Introduction to ASF+SDF 5 Introduction to ASF+SDF 6 Exam mple Exam mple trafo, top-down, continue trafo, bottom-up, continue frepl( g( g( 7, 8), 9)) frepl( g( g( 7, 8), 9)) i( i( 7, 8), 9) i( i( 7, 8), 9) frepl( ) p ( ) frepl( ) p ( ) g g g g i i i i frepl( ) frepl( ) g g 9 9 fr repl( ) fr repl( ) i i 9 9 frepl( ) p ( 7 ) frepl( ) p ( 8 ) frepl( ) p ( 7 ) frepl( ) p ( 8 ) 7 7 8 8 7 7 8 8 [1] frepl(g(T1, T2)) = i(T1, T2) [1] frepl(g(T1, T2)) = i(T1, T2) Introduction to ASF+SDF 7 Introduction to ASF+SDF 8
A real example: Co obol transformation A real example: Co obol transformation module End If Trafo module End-If-Trafo Add missing END-IF keywords END IF ● Cobol 75 has two forms s of conditional: imports Cobol exports – “IF” Expr “THEN” Sta p ts “END-IF”? context-free syntax context-free syntax addEndIf(Program)-> Program {traver rsal(trafo,continue,top- – “IF” Expr “THEN” stat ts “ELSE” Stats “END-IF”? down)} variables variables ● These are identical ( dan Th id ti l ( d ngling else problem): li l bl ) Impossible to do with regular "Stats"[0-9]* -> StatsOptIfNotClo osed expression tools like grep since "Expr"[0-9]* -> L-exp IF expr THEN IF expr THEN IF expr THEN "OptThen"[0 9]* > OptThen OptThen [0-9] -> OptThen conditionals can be nested conditionals can be nested IF expr THEN equations IF expr THEN [1] addEndIf(IF Expr OptThen Stats) = stats stats stats stats IF Expr OptThen Stats END I IF Expr OptThen Stats END-I IF IF Equations for the two cases ELSE ELSE [2] addEndIf(IF Expr OptThen Stats1 ELSE Stats2) = stats IF Expr OptThen Stats1 ELSE IF Expr OptThen Stats1 ELSE Stats2 END IF Stats2 END-IF stats Introduction to ASF+SDF 9 Introduction to ASF+SDF 10 A funny Pico o typechecker Exam mple begin ● Replace all variables by y their declared type: declare x : natural, Yields after typechecking: Yields after typechecking: – x +3 type(natural) + + type(natural) y : natural, s : string; begin ● Simplify type correct ex p y yp xpressions: p x : 10; s : abc ; x := 10; s := "abc"; declare; declare; if x then type(string) := type(natural); – type(natural) + type(na atural) type(natural) x := x + 1 end else ls ● Remove all type correct R ll t statements: s := x + 2 – type(natural) := type(n yp ( ) yp ( natural) fi; Erroneous statement leaves a residue Erroneous statement leaves a residue E E y := x + 2; ● A type correct program reduces to empty end ● Otherwise, only incorrec Oth i l i ct statements remain t t t t i Introduction to ASF+SDF 11 Introduction to ASF+SDF 12
Pico-type echeck (1) Pico-type echeck (2) Visit each variable declaration Vi it h i bl d l ti Extend identifiers so that we can and use replace to replace module Pico-typecheck equations replace them with type information imports Pico-syntax [0] begin declare Id-type, Decl*; Stat* e nd = the variable by its type exports begin declare Decl*; replace(Stat*, I d-type) context-free syntax end type(TYPE) -> ID Replace variables and Replace variables and replace(STATS, ID-TYPE) -> STATS {tr raversal(trafo,bottom-up,break)} [1] replace(Id , Id : Type) = type(Type) ) constants by their type replace(EXP , ID-TYPE) -> EXP {trave ersal(trafo,bottom-up,break)} [2] replace(Nat-con, Id : Type) = type(nat tural) [3] replace(Str-con, Id : Type) = type(str ring) Replace type-correct [4] type(string) || type(string) = type(str ring) repla ce . In the equations, the first argument expressions by their type The traversal function [5] type(natural) + type(natural) = type(na atural) may be of various sorts. Ea b f i t E ach variant that is h i t th t i used in the equations d i th ti [6] type(natural) - type(natural) = type(na atural) has to be declared here. Introduction to ASF+SDF 13 Introduction to ASF+SDF 14 Disambiguation v Disambiguation v via traversals (1) via traversals (1) Pico-type echeck (3) ● Semantic directed disamb S ti di t d di bi b biguation ti – Based on the concept of re ewriting parse forests. [7] Stat*1; if type(natural) then [7] Stat*1; if type(natural) then n Stat*2 else Stat*3 fi ; Stat*4 n Stat*2 else Stat*3 fi ; Stat*4 = Stat*1; Stat*2; Stat*3; St tat*4 – Applications ● C typedefs yp [8] Stat*1; while type(natural) d [8] Stat*1; while type(natural) d do Stat*2 od; Stat*3 do Stat*2 od; Stat*3 = Stat*1; Stat*2; Stat*3 ● Nested constructs in COBO OL [9] Stat*1; type(Type) : type(T [9] Stat*1; type(Type) := type(T Type); Stat*2 Type); Stat*2 = Stat*1; Stat*2 Remove type-correct expressions and statements Introduction to ASF+SDF 15 Introduction to ASF+SDF
Recommend
More recommend
