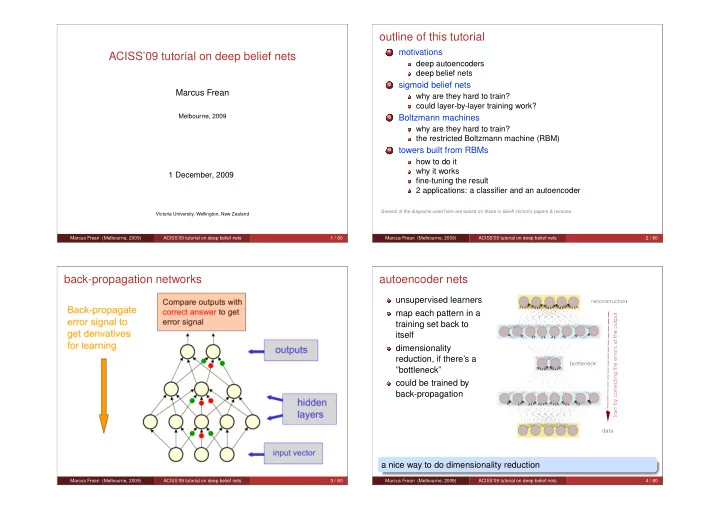

outline of this tutorial motivations 1 ACISS’09 tutorial on deep belief nets deep autoencoders deep belief nets sigmoid belief nets 2 Marcus Frean why are they hard to train? could layer-by-layer training work? Melbourne, 2009 Boltzmann machines 3 why are they hard to train? the restricted Boltzmann machine (RBM) towers built from RBMs 4 how to do it why it works 1 December, 2009 fine-tuning the result 2 applications: a classifier and an autoencoder Several of the diagrams used here are based on those in Geoff Hinton’s papers & lectures. Victoria University, Wellington, New Zealand Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 1 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 2 / 60 back-propagation networks autoencoder nets unsupervised learners map each pattern in a training set back to itself dimensionality reduction, if there’s a ”bottleneck” could be trained by back-propagation a nice way to do dimensionality reduction Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 3 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 4 / 60
why haven’t deep auto-encoders worked? belief nets all the hidden units interact A belief net is a directed acyclic graph composed of stochastic the gradient gets tiny as you variables move away from the ”output” We get to observe some of the layer variables and would like to solve two problems: The inference problem: Infer the 1 states of unobserved variables The learning problem: Adjust the 2 interactions between variables to make the network more likely to generate the observed data. too hard to learn Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 5 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 6 / 60 what would a really interesting generative model for parameterized belief networks (say) images look like? stochastic Large belief nets are still too lots of units powerful to learn with finite data. several layers But we can parameterize the easy to sample from factors: e.g. sigmoid function... sigmoid belief net an interesting generative model Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 7 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 8 / 60
stochastic neurons sampling from the joint input to the i th neuron: It is easy to sample from the prior p ( x ) = p ( h , v ) of a sigmoidal belief � φ i = w ji x j net: j p ( x ) = p ( x 1 , x 2 . . . x n ) probability of generating a 1: � = p ( x i | parents i ) i 1 p i = 1 + exp( φ i ) so we sample from each layer in turn, ending at the visible units. learning rule for making x more likely: it’s easy to make particular patterns ∆ w ji ∝ ( x i − p i ) x j more likely This seems like an attractive generative model. Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 9 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 10 / 60 but... Gibbs sampling to learn better weights based on a training To draw samples from p ( x ) = p ( x 1 , x 2 , . . . , x n ) : set, we need to generate samples from the posterior , not the prior choose i at random 1 choose x i from p ( x i | x \ i ) 2 joint = p ( h , v ) = ”generative model”: start at the top and sample from sigmoids posterior = p ( h | v ) = ”recognition model”: sample from hidden units, given the visible ones. how to draw such samples? adapted from David MacKay’s classic book filter from the generative model?// no! oh dear This results in a Markov Chain. Running the chain for long enough − → samples from p ( x ) . Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 11 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 12 / 60
Gibbs sampling in sigmoid belief nets explaining away Hidden states are So what does p ( x i | x \ i ) look like, in a sigmoid belief net? independent in the prior dependent in the posterior two hidden ”causes” That dependence means sampling from visible node is observed... one hidden unit has to cause a change Gibbs sampling for h 1 , h 2 : in how all other hidden units update their states. � � − 1 1 + (1 − f ( b 1 )) f ( w 2 ) p ( h 1 = 1 | v = 1) = f ( b 1 ) f ( w 1 + w 2 ) But we are interested in nets with lots of = yuck! hidden units. Gibbs sampler in sigmoid belief net: an inconvenient truth: ugly, slow there’s no quick way to draw a sample from p ( hidden | visible ) reason is ’explaining away’ Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 13 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 14 / 60 sigmoidal belief nets are: building a deep BN layer-by-layer Easy to sample from as a generative model, but hard to learn Here’s a way to train a multilayer sigmoid belief net: sampling from the posterior is slow, due to explaining away. This 1 start with a single layer only. The hidden 1 also makes them hard to use for recognition. units are driven by bias inputs only. Train ‘deep’ layers learn nothing until the ‘shallow’ ones have settled, 2 to maximize the likelihood of generating but shallow layers have to learn while being driven by the deep the training data. layers (chicken and egg...) freeze the weights in that layer, and 2 replace the hidden units’ bias inputs by a second layer of weights. Let’s ignore the quibbles about slowness for a moment, and consider train the second layer of weights to this idea: one way around the second difficulty might be to train the 3 maximize the likelihood. first layer as a simple BN first, and then the second layer, and so on. and so on... 4 Question: what should the training set be for the second layer? Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 15 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 16 / 60
the EM algorithm the EM algorithm, via sampling The W 1 weights, and the biases In practice we can’t work with into the hidden units, are the posterior p ( h | v ) trained so as to maximize the analytically: we have to sample probability of generating the from it instead. patterns on visible units in a data set. For each v in the training data: E step: draw a sample from p ( h | v ) The EM algorithm achieves this by repeating two steps, for each v in the training data: M step: move the W 1 weights so as to make v more likely, given that h . E step: calculate p ( h | v ) Move the hidden biases to better produce that h . M step: move the W 1 weights so as to make v more likely, under p ( h | v ) . And move the hidden biases to better produce that distribution. Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 17 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 18 / 60 aggregate posterior training the next layer Averaging over the training set, Q: what is the best thing that the we have an aggregate posterior second layer could learn to do? distribution: A: accurately generate the aggre- gate posterior distribution over the � p agg ( h ) = p ( h | v ) layer 1 hidden units. It is the distri- v ∈D bution that makes the training data most likely, given W 1 So the W 1 weights end up at values that maximize the likelihood of the data, given h sampled from the aggregate posterior distribution. Easy! For each visible pattern, we just collect one sample (or The hidden bias weights end up at values that approximate this more) from p ( h | v ) . distribution. This gives us a greedy, layer-wise procedure for training deep belief nets. Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 19 / 60 Marcus Frean (Melbourne, 2009) ACISS’09 tutorial on deep belief nets 20 / 60
Recommend
More recommend