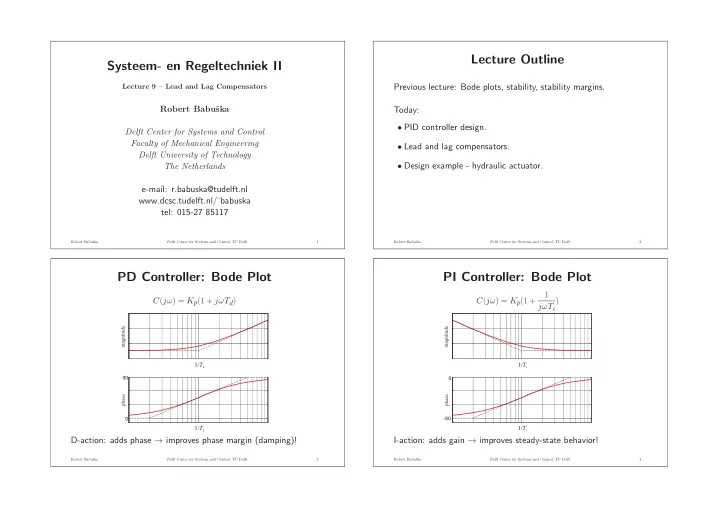
Lecture Outline Systeem- en Regeltechniek II Previous lecture: Bode - PowerPoint PPT Presentation

Lecture Outline Systeem- en Regeltechniek II Previous lecture: Bode plots, stability, stability margins. Lecture 9 – Lead and Lag Compensators Robert Babuˇ ska Today: • PID controller design. Delft Center for Systems and Control Faculty of Mechanical Engineering • Lead and lag compensators. Delft University of Technology • Design example - hydraulic actuator. The Netherlands e-mail: r.babuska@tudelft.nl www.dcsc.tudelft.nl/ ˜ babuska tel: 015-27 85117 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 1 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 2 PD Controller: Bode Plot PI Controller: Bode Plot 1 C ( jω ) = K p (1 + jωT d ) C ( jω ) = K p (1 + ) jωT i magnitude magnitude 1/ T d 1/ T i 90 0 phase phase 0 -90 1/ T d 1/ T i D-action: adds phase → improves phase margin (damping)! I-action: adds gain → improves steady-state behavior! Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 3 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 4

PID Controller PID Controller: Bode Plot C = K p ( T i s + 1)( T d s + 1) Parallel form (see earlier lectures): T i s � � 1 + 1 C ( s ) = K p T i s + T d s magnitude Serial form (more commonly used in FD design): � 1 + 1 � 1/ T i 1/ T d C ( s ) = K p (1 + T d s ) T i s 90 = K p ( T i s + 1)( T d s + 1) phase T i s -90 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 5 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 6 PID Controller Design Example: PD Satellite Attitude Control • Adjust the proportional gain to get the required crossover fre- quency and/or steady-state tracking error. • If needed, use the derivative action to add phase in the neigh- borhood of ω c in order to increase the phase margin. • If needed, use the integral action to increase the gain at low fre- quencies in order to guarantee the required steady-state tracking Transfer function: G ( s ) = Θ( s ) T ( s ) = 1 error. s 2 Performance specs: bandwidth of ≈ 0 . 2 rad/s, good damping. Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 7 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 8

Drawbacks of the PID Controller Lead and Lag Compensation • The derivative action introduces very large gain for high fre- Lead compensator: quencies (noise amplification). C lead ( s ) = T lead s + 1 α < 1 αT lead s + 1 • The integral action introduces infinite gain for zero frequency (it is open-loop unstable) if the loop is broken. Lag compensator: C lag ( s ) = β T lag s + 1 β > 1 magnitude βT lag s + 1 1/ T i 1/ T d Lead-lag compensator: 90 T (lead s + 1)( T lag s + 1) phase C ( s ) = β ( αT lead s + 1)( βT lag s + 1) -90 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 9 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 10 Lead Compensator: Bode Plot Lead Compensator vs. PD Controller magnitude magnitude 0 0 Ts + 1 Ts + 1 1/ T 1/ T αTs + 1 αTs + 1 90 90 phase phase 0 0 1/ T 1/ T Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 11 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 12

Lead Compensator – Maximal Phase Lead Lag Compensator: Bode Plot 90 � magnitude phase 0 β Ts + 1 1/ � T 1/ T βTs + 1 1/ T 0 phase 1 sin φ max = 1 − α α = 1 − sin φ max ω max = T √ α ⇒ 1 + α 1 + sin φ max -90 1/ T 1/ � T Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 13 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 14 Lag Compensator vs. PI Controller Lead-Lag Compensator: Bode Plot � � magnitude magnitude β Ts + 1 1/ � T 1/ T βTs + 1 0 90 phase phase -90 1/ T -90 1/ � T Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 15 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 16

Closed Loop Control Lead Compensator Design 1. Determine the crossover frequency. Typically: Closed loop TF: G ( s ) D ( s ) K ω c ≤ ω bw ≤ 2 ω c G cl ( s ) = 1 + G ( s ) D ( s ) K 2. Calculate how much extra phase must be added by the lead compensator at the crossover frequency. Compute: D ( s ) is either the lead, the lag or the lead-lag compensator √ α α = 1 − sin φ max 1 = ω c 1 + sin φ max T lead – lead compensator = realistic PD controller 3. Compute the overall controller gain K such that the required – lag compensator = gain-limited PI controller ω c is obtained. 4. Check whether the specs are met, if not, revise choices. Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 17 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 18 Lag Compensator Design Design Example: Hydraulic Actuator 1. Determine the crossover frequency. Typically: Load ω c ≤ ω bw ≤ 2 ω c 2. Determine β to meet the steady-state requirements. Servo valve � � 1 1 x 3. Choose T lag ∈ , . i 0 . 5 ω c 0 . 1 ω c Q 4. Check whether the specs are met, if not, revise choices, iterate on the design. p s Oil pump Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 19 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 20

Hydraulic Actuator – Physical Model Hydraulic Actuator – Control Specs M ¨ x + b ˙ x + Mg = A p p closed-loop bandwidth: ω bw ≈ 40 rad / s V PM ≈ 60 ◦ phase margin: p + L e p + A p ˙ ˙ x = Q E o steady-state ramp tracking error: e ss ≤ 0 . 01 m / s   � 1 − | p | Q + τ ˙  i Q =  K v p s rise time: t r = 1 . 8 /ω bw ≈ 0 . 045 s relative damping: x – piston position (to be controlled) ζ ≈ PM / 100 ≈ 0 . 6 − πζ √ p – oil pressure in the cylinder 1 − ζ 2 ≈ 10 % overshoot: M p = e Q – oil flow-rate crossover frequency: ω c = ω bw / 2 ≈ 20 rad / s i – servo valve current (control input) Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 21 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 22 Hydraulic Actuator – Linearized Model Bode Plot of Loop TF Bode Diagram 50 G ( s ) = X ( s ) 5574416 I ( s ) = 0 s ( s + 25)( s 2 + 91 . 53 s + 8068) Magnitude (dB) −50 −100 −150 System type: 1 (one pure integrator) −200 −90 K v = 5574416 / (25 · 8068) = 27 . 58 System: G −180 Frequency (rad/sec): 20 Phase (deg) Phase (deg): −142 Steady-state error for ramp: 1 /K v = 0 . 036 −270 Required steady-state error: 0 . 01 −360 0 1 2 3 4 10 10 10 10 10 Frequency (rad/sec) Phase( ω c )= 180-142 = 38 deg → additional 22 deg needed. Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 23 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 24

Lead Compensator Design Lead-Compensated Loop TF Bode Diagram Take additional phase of 27 deg (extra margin of 5 deg): 50 α = 1 − sin(27 π/ 180) 0 Magnitude (dB) 1 + sin(27 π/ 180) = 0 . 375 System: untitled2 Frequency (rad/sec): 20.1 Magnitude (dB): −0.0395 −50 √ α 1 = ω c → T lead = 0 . 08 s −100 T lead −90 −180 Phase (deg) C lead = T lead s + 1 αT lead s + 1 = 0 . 08 s + 1 −270 0 . 03 s + 1 −360 0 1 2 3 10 10 10 10 Frequency (rad/sec) K = 1 / | G ( jω c ) C lead ( jω c ) | = 0 . 553 K = 0.553 (-5.11 dB). Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 25 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 26 Lag Compensator Design Lag Compensator Design The lead compensator satisfies the bandwidth and PM specs. C lag ( s ) = β T lag s + 1 However, it cannot meet the steady-state error requirement e ss = β > 1 βT lag s + 1 0 . 01 : Additional steady-state gain β = 0 . 0653 / 0 . 01 = 6 . 53 . s ( s + 25)( s 2 + 91 . 53 s + 8068) · 0 . 08 s + 1 5574416 G ( s ) C lead ( s ) K = 0 . 03 s + 1 · 0 . 553 Choose T lag = 1 / (0 . 1 ω c ) = 0 . 5 s (rule of thumb) C lag ( s ) = 6 . 53 · 0 . 5 s + 1 K v = 5574416 · 0 . 553 / (25 · 8068) = 15 . 32 3 . 27 s + 1 e ss = 1 = 0 . 0653 K v Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 27 Robert Babuˇ ska Delft Center for Systems and Control, TU Delft 28