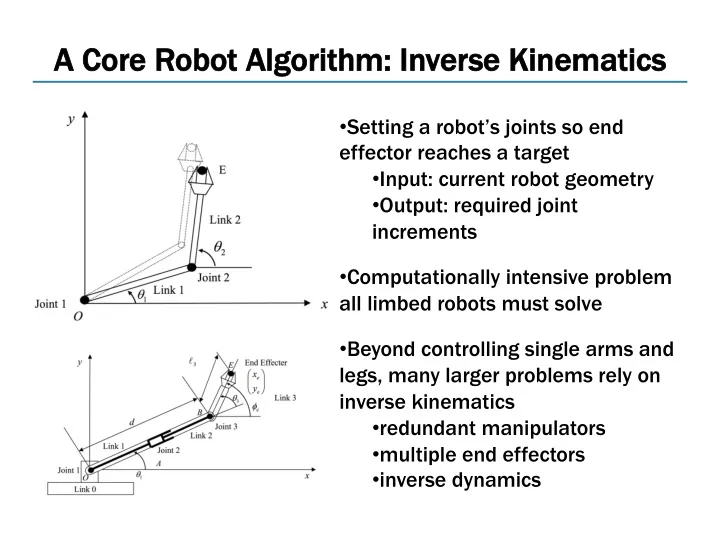
A C A Core R Robot Al Algorithm hm: I Inverse K Kinematics - PowerPoint PPT Presentation

A C A Core R Robot Al Algorithm hm: I Inverse K Kinematics • Setting a robot’s joints so end effector reaches a target • Input: current robot geometry • Output: required joint increments • Computationally intensive problem all limbed robots must solve • Beyond controlling single arms and legs, many larger problems rely on inverse kinematics • redundant manipulators • multiple end effectors • inverse dynamics 1

A D A Digital A Accelerator f for I Inverse K Kinematics • Inverse kinematics not well suited for normal digital architectures – Entirely floating point array, matrix operations – 40% of cycles in inverting matrices – 15% of cycles in sine, cosine operations • We solve IK via damped least squares – Dedicated sine, cosine function generators – Parallel, fixed-point functional units – Solves IK problem in 100µs: compare against 10ms for general algorithm on CPU 2

Archi Ar hitecture a and Toolcha hain ROS URDF Collada D-H Params cpp-inverse- FPGA kinematics- CONFIGURATION library Robot TIME Geometry Compiler XML matrix constants d d A A*sin( Θ ) A A*cos( Θ ) Θ sin( Θ ) sin( Θ )sin( α ) Θ cos( Θ ) -sin( Θ )cos( α ) α sin( α ) -cos( Θ )sin( α ) α cos( α ) cos( Θ )cos( α ) 16 4x4 Matrix Multiplier FPGA Forward Forward Inverse ... 16 16 Kinematics Kinematics Kinematics 16 RUNTIME • axis of rot. / trans. • pos. & rot. of joint Matrix Jacobian Matrix Jacobian Finder Full Matrix Jacobian Damped Least Mult. Pipeline Block Squares Block variables LINUX Robot Incremental RUNTIME Current Joint Target Pose Joint Actions Pose 3

Ar Archi hitecture a and T Timing D Design • Architectural Choices • Pipelining sine/cosine and array multiply • Parallelized matrix multiply and matrix inversion • Fixed point representations throughout system • Timing Choices • Single array of multipliers shared amongst modules • Aggregate individual enable and done signals into global state machine 4

Experiences a and I Issues • Deciding on the algorithm to use • Determining what implementation would fit on the board • Convincing ourselves the algorithm works • Extensively tested the core hardware, but not the top-level interface (until yesterday) 5

Lessons L Learned • Test the whole stack earlier • Plan before trying to implement • Use timing diagrams and area estimates before touching hardware • Leave no ambiguity in the design 6