W j,i a j a i Chapter 20, Section 5 Input Input Activation - PDF document

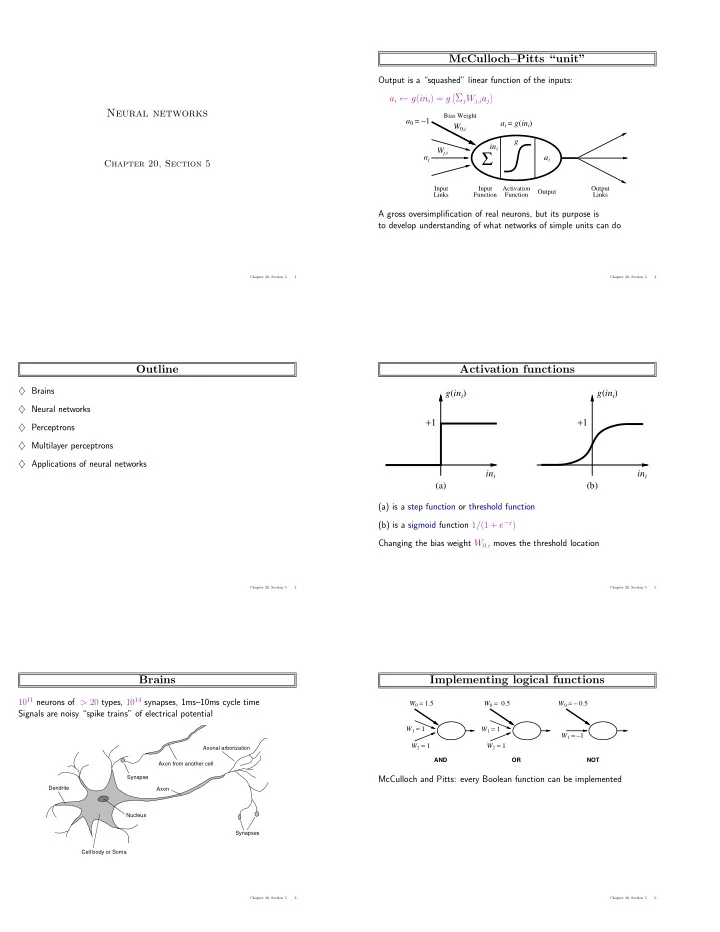
McCulloch–Pitts “unit” Output is a “squashed” linear function of the inputs: � Σ j W j,i a j � a i ← g ( in i ) = g Neural networks Bias Weight a 0 = − 1 a i = g ( in i ) W 0 ,i g in i Σ W j,i a j a i Chapter 20, Section 5 Input� Input� Activation� Output� Output Links Function Function Links A gross oversimplification of real neurons, but its purpose is to develop understanding of what networks of simple units can do Chapter 20, Section 5 1 Chapter 20, Section 5 4 Outline Activation functions ♦ Brains g ( in i ) g ( in i ) ♦ Neural networks + 1 + 1 ♦ Perceptrons ♦ Multilayer perceptrons ♦ Applications of neural networks in i in i (a)� (b)� (a) is a step function or threshold function (b) is a sigmoid function 1 / (1 + e − x ) Changing the bias weight W 0 ,i moves the threshold location Chapter 20, Section 5 2 Chapter 20, Section 5 5 Brains Implementing logical functions 10 11 neurons of > 20 types, 10 14 synapses, 1ms–10ms cycle time W 0 = 1.5 W 0 = 0.5 W 0 = – 0.5 Signals are noisy “spike trains” of electrical potential W 1 = 1 W 1 = 1 W 1 = –1 W 2 = 1 W 2 = 1 Axonal arborization AND OR NOT Axon from another cell Synapse McCulloch and Pitts: every Boolean function can be implemented Dendrite Axon Nucleus Synapses Cell body or Soma Chapter 20, Section 5 3 Chapter 20, Section 5 6

Network structures Expressiveness of perceptrons Feed-forward networks: Consider a perceptron with g = step function (Rosenblatt, 1957, 1960) – single-layer perceptrons Can represent AND, OR, NOT, majority, etc., but not XOR – multi-layer perceptrons Represents a linear separator in input space: Feed-forward networks implement functions, have no internal state Σ j W j x j > 0 or W · x > 0 Recurrent networks: – Hopfield networks have symmetric weights ( W i,j = W j,i ) x 1 x 1 x 1 g ( x ) = sign ( x ) , a i = ± 1 ; holographic associative memory 1 1 1 – Boltzmann machines use stochastic activation functions, ≈ MCMC in Bayes nets ? – recurrent neural nets have directed cycles with delays 0 0 0 ⇒ have internal state (like flip-flops), can oscillate etc. x 2 x 2 x 2 0 1 0 1 0 1 (a) x 1 and x 2 (b) x 1 or x 2 (c) x 1 xor x 2 Minsky & Papert (1969) pricked the neural network balloon Chapter 20, Section 5 7 Chapter 20, Section 5 10 Feed-forward example Perceptron learning Learn by adjusting weights to reduce error on training set W 1,3 1 3 The squared error for an example with input x and true output y is W 3,5 W E = 1 2 Err 2 ≡ 1 1,4 2( y − h W ( x )) 2 , 5 Perform optimization search by gradient descent: W ∂E = Err × ∂ Err ∂ W 2,3 y − g ( Σ n � � 4,5 = Err × j = 0 W j x j ) 2 4 ∂W j ∂W j ∂W j W 2,4 = − Err × g ′ ( in ) × x j Simple weight update rule: Feed-forward network = a parameterized family of nonlinear functions: W j ← W j + α × Err × g ′ ( in ) × x j a 5 = g ( W 3 , 5 · a 3 + W 4 , 5 · a 4 ) = g ( W 3 , 5 · g ( W 1 , 3 · a 1 + W 2 , 3 · a 2 ) + W 4 , 5 · g ( W 1 , 4 · a 1 + W 2 , 4 · a 2 )) E.g., +ve error ⇒ increase network output ⇒ increase weights on +ve inputs, decrease on -ve inputs Adjusting weights changes the function: do learning this way! Chapter 20, Section 5 8 Chapter 20, Section 5 11 Single-layer perceptrons Perceptron learning contd. Perceptron learning rule converges to a consistent function for any linearly separable data set Perceptron output Proportion correct on test set Proportion correct on test set 1 1 1 0.8 0.9 0.9 0.6 0.8 0.8 0.4 0.2 0.7 0.7 -4 -2 0 2 4 0 x 2 -4 0.6 Perceptron 0.6 Output -2 Input 0 2 Decision tree W j,i x 1 4 0.5 0.5 Perceptron Units Units Decision tree 0.4 0.4 0 10 20 30 40 50 60 70 80 90 100 0 10 20 30 40 50 60 70 80 90 100 Output units all operate separately—no shared weights Training set size - MAJORITY on 11 inputs Training set size - RESTAURANT data Adjusting weights moves the location, orientation, and steepness of cliff Perceptron learns majority function easily, DTL is hopeless DTL learns restaurant function easily, perceptron cannot represent it Chapter 20, Section 5 9 Chapter 20, Section 5 12

Multilayer perceptrons Back-propagation derivation Layers are usually fully connected; The squared error on a single example is defined as numbers of hidden units typically chosen by hand E = 1 i ( y i − a i ) 2 , � Output units 2 a i where the sum is over the nodes in the output layer. W j,i ∂E = − ( y i − a i ) ∂a i = − ( y i − a i ) ∂g ( in i ) ∂W j,i ∂W j,i ∂W j,i Hidden units a j = − ( y i − a i ) g ′ ( in i ) ∂ in i ∂   = − ( y i − a i ) g ′ ( in i ) j W j,i a j �     ∂W j,i ∂W j,i W = − ( y i − a i ) g ′ ( in i ) a j = − a j ∆ i k,j Input units a k Chapter 20, Section 5 13 Chapter 20, Section 5 16 Expressiveness of MLPs Back-propagation derivation contd. All continuous functions w/ 2 layers, all functions w/ 3 layers ∂E i ( y i − a i ) ∂a i i ( y i − a i ) ∂g ( in i ) = − = − � � ∂W k,j ∂W k,j ∂W k,j h W ( x 1 , x 2 ) h W ( x 1 , x 2 ) i ( y i − a i ) g ′ ( in i ) ∂ in i ∂   = − = − i ∆ i j W j,i a j 1 1 � � �     ∂W k,j ∂W k,j 0.8 0.8 0.6 0.6 ∂a j ∂g ( in j ) 0.4 0.4 = − i ∆ i W j,i = − i ∆ i W j,i � � 0.2 0.2 ∂W k,j ∂W k,j -4 -2 0 2 4 -4 -2 0 2 4 0 0 x 2 x 2 -4 -4 -2 -2 i ∆ i W j,i g ′ ( in j ) ∂ in j 0 0 2 2 x 1 4 x 1 4 = − � ∂W k,j ∂   = − i ∆ i W j,i g ′ ( in j ) k W k,j a k � �   Combine two opposite-facing threshold functions to make a ridge   ∂W k,j i ∆ i W j,i g ′ ( in j ) a k = − a k ∆ j = − � Combine two perpendicular ridges to make a bump Add bumps of various sizes and locations to fit any surface Proof requires exponentially many hidden units (cf DTL proof) Chapter 20, Section 5 14 Chapter 20, Section 5 17 Back-propagation learning Back-propagation learning contd. Output layer: same as for single-layer perceptron, At each epoch, sum gradient updates for all examples and apply W j,i ← W j,i + α × a j × ∆ i Training curve for 100 restaurant examples: finds exact fit 14 where ∆ i = Err i × g ′ ( in i ) Total error on training set 12 Hidden layer: back-propagate the error from the output layer: 10 8 ∆ j = g ′ ( in j ) i W j,i ∆ i . � 6 4 Update rule for weights in hidden layer: 2 W k,j ← W k,j + α × a k × ∆ j . 0 0 50 100 150 200 250 300 350 400 (Most neuroscientists deny that back-propagation occurs in the brain) Number of epochs Typical problems: slow convergence, local minima Chapter 20, Section 5 15 Chapter 20, Section 5 18

Back-propagation learning contd. Learning curve for MLP with 4 hidden units: 1 Proportion correct on test set 0.9 0.8 0.7 0.6 Decision tree Multilayer network 0.5 0.4 0 10 20 30 40 50 60 70 80 90 100 Training set size - RESTAURANT data MLPs are quite good for complex pattern recognition tasks, but resulting hypotheses cannot be understood easily Chapter 20, Section 5 19 Handwritten digit recognition 3-nearest-neighbor = 2.4% error 400–300–10 unit MLP = 1.6% error LeNet: 768–192–30–10 unit MLP = 0.9% error Current best (kernel machines, vision algorithms) ≈ 0.6% error Chapter 20, Section 5 20 Summary Most brains have lots of neurons; each neuron ≈ linear–threshold unit (?) Perceptrons (one-layer networks) insufficiently expressive Multi-layer networks are sufficiently expressive; can be trained by gradient descent, i.e., error back-propagation Many applications: speech, driving, handwriting, fraud detection, etc. Engineering, cognitive modelling, and neural system modelling subfields have largely diverged Chapter 20, Section 5 21