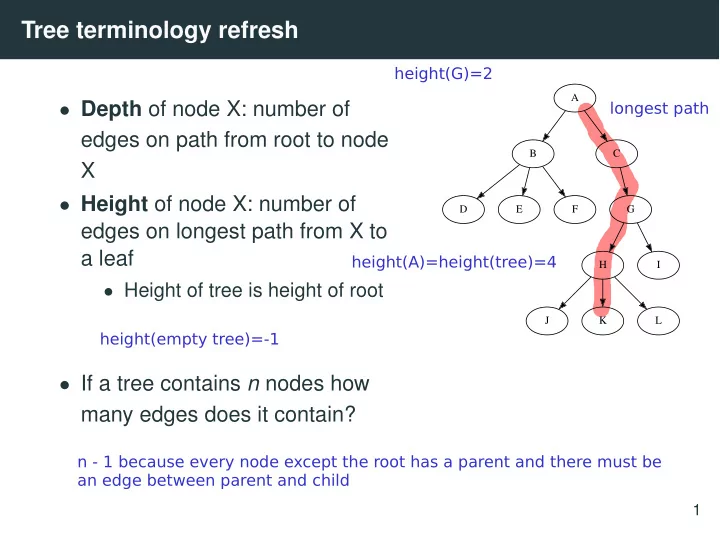

Tree terminology refresh height(G)=2 A longest path • Depth of node X: number of edges on path from root to node B C X • Height of node X: number of D E F G edges on longest path from X to a leaf height(A)=height(tree)=4 H I • Height of tree is height of root J K L height(empty tree)=-1 • If a tree contains n nodes how many edges does it contain? n - 1 because every node except the root has a parent and there must be an edge between parent and child 1
d-ary trees d -ary: Every node has at most d children (binary d = 2) Recursive de fi nition: A d-ary tree is either an empty tree OR A A root (node) with at most d child trees which are d-ary trees themselves. B C Aside: If we consider empty trees we could say every node has exactly d children, some empty some "real" D E F G H I J K L full full d -ary tree: every node has 0 or d nodes perfect d -ary tree: maximum nodes for height (all non-leafs perfect have d children and leafs have 0) complete d -ary tree: each level except possibly deepest fi lled full all nodes in deepest level as far to left as possible 2 This will make more sense when we see the implementation
Recursive trees Recursive de fi nition of height: height(empty)=-1 A height(T)=1 + height( ) + height( ) T R T L B C T R D E F G T L H I J K L M N O Number of nodes in a perfect binary tree of height h ? h=1 h=0 h=2 h=k =2 (2^(h-1+1) - 1) + 1 1 =2 (2^h) - 2 + 1 3 2 ( k +1) − 1 7 =2^(h+1) - 1 Proof: Let N(h) be the number of nodes in a perfect tree of height h. Base case: N(0)=1 Recursion: N(h) = 2N(h - 1) + 1 Because we have root plus two children that are perfect. Induction hypothesis: N(k) = 2^(k+1) - 1 for all k < h 3 By I.H. and recursion: N(h)=2N(h-1)+1
Counting empty trees with n nodes? How many empty trees hang off a binary tree of heigh h ? Every node has 2 children "real" or empty. So there are 2n real or empty children in the tree. A Every real node except the root is a child => n - 1 B C real children F G D E Thus there are n+1 empty children J K H I Proof: By induction next class. L Empty children You can think of empty nodes/trees as NULL pointers. 4
Ordered binary tree ADT BEE • Ordered binary tree node can have left and right children EMU ANT • Recursively: either empty or o o a root with left and right children which are ordered CAT DOG o o o o binary trees template < class T> Tree ADT class tree{ • Insert node public : ... • Remove node private : struct Node{ • Traverse T data; Node * left; Node * right;}; Node * root; ...}; 5
Tree traversal 10 inOrderTraversal(Node * n){ if (n != NULL){ 5 15 2 9 20 inOrderTraversal(n->left); 7 17 30 In order: inOrderTraversal(n->right); 2, 5, 9, 7, 10, 15, 17, 20, 30 }} 6
Recommend
More recommend