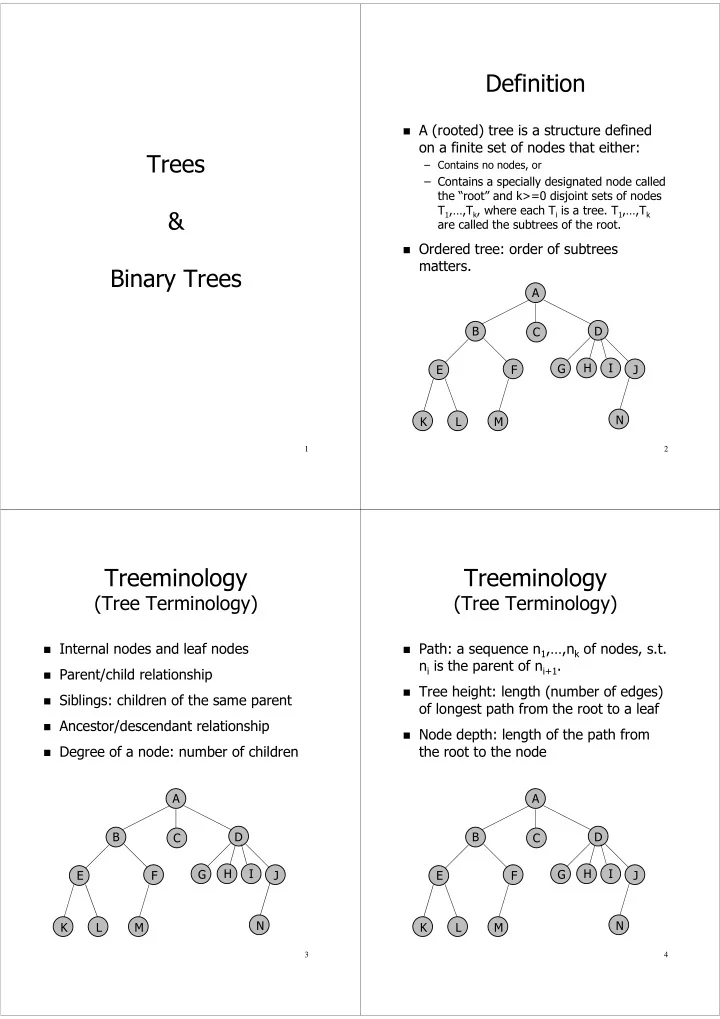
Definition ! A (rooted) tree is a structure defined on a finite set - PDF document

Definition ! A (rooted) tree is a structure defined on a finite set of nodes that either: Trees – Contains no nodes, or – Contains a specially designated node called the “root” and k>=0 disjoint sets of nodes T 1 ,…,T k , where each T i is a tree. T 1 ,…,T k & are called the subtrees of the root. ! Ordered tree: order of subtrees matters. Binary Trees A B D C H I G E F J N K L M 1 2 Treeminology Treeminology (Tree Terminology) (Tree Terminology) ! Internal nodes and leaf nodes ! Path: a sequence n 1 ,…,n k of nodes, s.t. n i is the parent of n i+1 . ! Parent/child relationship ! Tree height: length (number of edges) ! Siblings: children of the same parent of longest path from the root to a leaf ! Ancestor/descendant relationship ! Node depth: length of the path from ! Degree of a node: number of children the root to the node A A B D B D C C H I H I G G E F J E F J N N K L M K L M 3 4

Binary Trees More Terminology ! A binary tree T is a structure defined ! A full binary tree: each node has either on a finite set of nodes that either degree 0 (a leaf) or 2 (has exactly two non-empty children). – Contains no nodes, or – Is comprised of a root node, and two ! A complete binary tree: a full binary subtrees (left and right) each of which is tree in which all leaves have the same also a binary tree. depth. A A full: complete: A A B C B C ≠ B C B C D E F D E F D E D E F G G G F G 5 6 Treevia (Tree Facts) Array Implementation ! How many leaf nodes are there in a A complete binary tree of height h? B C ! What is the number of internal nodes in such a tree? D E F G ! What is the total number of nodes? ! How many leaf nodes are there in a A B C D E F G full binary tree of height h? ! How tall can a full binary tree with n leaf nodes be? 7 8

Pointer-Based Array Implementation Implementation class BinaryTreeA { class BinaryTree { private int size; private Item item; private Item[] items; // 0..size-1 private BinaryTree left, right; int leftChild(int i) { BinaryTree leftChild() { return 2*i + 1; return left; } } int rightChild(int i) { BinaryTree rightChild() { return 2*i + 2; return right; } } int parent(int i) { boolean isLeaf() { return floor((i - 1) / 2); return (left == null && } right == nul); } } } 9 10 Binary Tree Traversal ! Inorder: visit left subtree, then the root, then the right subtree. ! Preorder: visit root, left, right. ! Postorder: visit left, right, root. void inOrder(BinaryTree t) { if (t.leftChild() != null) inOrder(t.leftChild()); doStuff(t); if (t.rightChild() != null) inOrder(r.rightChild()); } 11