Real-time Animation and Real-time Animation and Rendering of Ocean - PowerPoint PPT Presentation

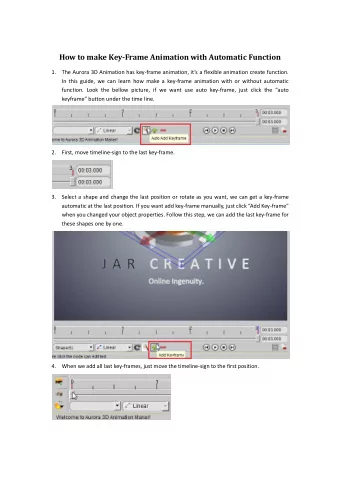
Real-time Animation and Real-time Animation and Rendering of Ocean Whitecaps Rendering of Ocean Whitecaps Jonathan Dupuy, Eric Bruneton INRIA Grenoble Rhône-Alpes, Université de Grenoble et CNRS, Laboratoire Jean Kuntzmann Université de Lyon, CNRS Université Lyon 1, LIRIS, UMR5205, F-69622, France

Whitecaps Whitecaps spume + foam streaks foam streaks + surface foam surface foam + bubble cloud bubble cloud spume 2

Deep Water Breaking Waves Deep Water Breaking Waves Plunging breaker Spilling breaker 3

Motivation Motivation Real time Photographs Movies 4

Ocean Rendering: Wave Models Ocean Rendering: Wave Models Trochoidal waves Fourier transform [Tessendorf 2001] [Hinsinger et al. 2002] [Tessendorf 2001] [Hinsinger et al. 2002] ocean surface = horizontally and vertically undulated plane ocean surface ocean plane displacement 5

Ocean Rendering: Lighting Ocean Rendering: Lighting [Bruneton et al. 2010] [Bruneton et al. 2010] mean position position + mean normal normal + slope variance variance 6

Ocean Rendering: Whitecaps Ocean Rendering: Whitecaps Particle based Empirical models [Chentanez and Müller 2011] [Darles et al. 2007] [Darles et al. 2007] [Chentanez and Müller 2011] whitecaps whitecaps sim. domain no whitecaps no whitecaps low quality no control / slow 7

Objective Objective ● Extend Bruneton's lighting model to account for whitecaps – Any viewpoint from ground to space – Seamless transitions from geometry to BRDF – Real time ● Context – Deep water waves – Gaussian heights and slopes – Spilling breakers only (no overturning) 8

Ocean Lighting Ocean Lighting [Bruneton et al. 2010] [Bruneton et al. 2010] ● ● Whitecap radiance depends on amount of breaking waves 9

Breaking Waves Breaking Waves ● Use surface tension – Proportional to jacobian of horizontal displacements illustrative only wave profile wave profile 10

Breaking Waves Breaking Waves ● We use 11

Breaking Waves Breaking Waves ● Use surface tension – Proportional to jacobian of horizontal displacements illustrative only wave profile wave profile 12

Breaking Waves Breaking Waves ● Use surface tension – Proportional to jacobian of horizontal displacements illustrative only wave profile wave profile 13

Breaking Waves Breaking Waves ● We use ● depends on Gaussian functions parameters can be computed analytically for trochoids or through hardware mipmapping for Fourier waves 14

Ocean Lighting Ocean Lighting [Bruneton et al. 2010] [Bruneton et al. 2010] ● ● Whitecap radiance depends on amount of breaking waves 15

Ocean Lighting Ocean Lighting ● ● Whitecap radiance depends on amount of breaking waves 16

Results: Quality Results: Quality real time photographs 17

Results: Control Results: Control (same surface) 18

Results: Scalability / Real Time Results: Scalability / Real Time NVidia GeForce 560Ti 19

Results: Limitations Results: Limitations ● Reflectance fluctuations only – No impact on geometry ex: no plunging breakers ● No decay – Whitecap can last several seconds ● Analytical surface – Repetitive artifacts on periodic surfaces 20

Conclusion Conclusion ● Ocean scenes with whitecaps in real time – Scalable performance – Controlable – Good quality ● Future work – Decay – Richer whitecap shading model (currently Lambertian / no visibility) 21

Real-time Animation and Real-time Animation and Rendering of Ocean Whitecaps Rendering of Ocean Whitecaps Jonathan Dupuy, Eric Bruneton INRIA Grenoble Rhône-Alpes, Université de Grenoble et CNRS, Laboratoire Jean Kuntzmann Université de Lyon, CNRS Université Lyon 1, LIRIS 22

Projected Grid Projected Grid ● Automatic geometrical LOD eye reprojected vertex reconstructed surface ocean plane 23

Projected Grid Projected Grid ● Automatic geometrical LOD eye reprojected vertex reconstructed surface ocean plane 24

Erf: Approximation Erf: Approximation erf(x) our approximation 25

Erf: Error Erf: Error max error: 0.00012 26