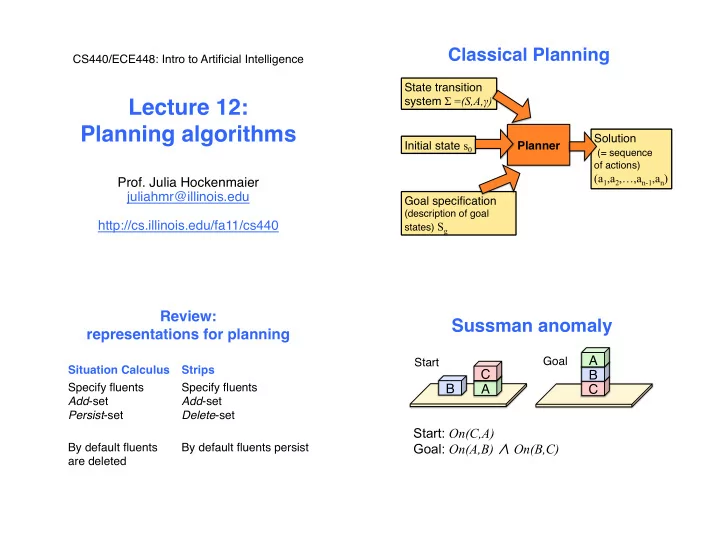

Classical Planning � CS440/ECE448: Intro to Artificial Intelligence � State transition system ! = (S,A, ! ) Lecture 12: Planning algorithms � Solution Initial state s 0 � Planner � (= sequence of actions) � (a 1 ,a 2 ,…,a n-1 ,a n ) � Prof. Julia Hockenmaier � juliahmr@illinois.edu � Goal specification � � (description of goal http://cs.illinois.edu/fa11/cs440 � states) S g � � � Review: Operators � Sussman anomaly � representations for planning � A � Goal � Start � Situation Calculus � Strips � C � B � Specify fluents Specify fluents � B � A � C � Add -set Add -set � Persist -set � Delete -set � � Start: On(C,A) Goal: On(A,B) ∧ On(B,C) By default fluents By default fluents persist � are deleted �
A � A � C � C � B � B � B � A � B � A � C � C � Start: On(C,A) Goal: On(A,B) ∧ On(B,C) Start: On(C,A) Goal: On(A,B) ∧ On(B,C) Solve On(A,B) first: Solve On(B,C) first: A � B � B � B � A � B � C � A � C � C � C � C � B � A � A � B � C � A � A � A � B � B � B � B � C � C � A � C � C � A � A � C � B � Planning algorithms � B � A � C � State space search (DFS, BFS, etc.) � Start: On(C,A) Goal: On(A,B) ∧ On(B,C) Nodes = states; edges = actions; � Heuristics (make search more efficient) � Most efficient solution requires interleaved planning: Compute h() using relaxed version of the problem � Plan space search (refinement of partial plans) � B � A � C � Nodes = partial plans; edges: fix flaws in plan � B � SATplan (encode plan in propositional logic) � C � A � Solution = true variables in a model for the plan � A � B � Graphplan (reduce search space to planning graph) � C � Planning graph: levels = literals and actions � CS440/ECE448: Intro AI � 8 �
Planning as state space search � Search tree: � – Nodes: states � – Root: initial state � – Edges: actions (ground instances of operators � State space search � – Solutions: paths from initial state to goal. � I,a4 � I,a2 � I,a4,a3 � I � I,a2,a34 � I,a15 � I,a15,a4 � I,a17 � DFS and loops: Forward search � iterative deepening � Initial State � Loops ( s i " … " s i ) in the search graph lead ... � to infinite branches in the search tree. � � ... � The tree-search variant of DFS never Breadth-first forward search is sound and terminates if it goes down an infinite branch � complete, but may require lots of memory � � � Remedy (iterative deepening): � Depth-first forward search can be better in – Try to find solution of length l with DFS � practice (needs graph-search to be complete) � � – If this fails, l := l + # ; try again. Problem: branching factor is very large (need good heuristic: which actions may lead to goal?) � CS440/ECE448: Intro AI � 12 �
Backward search � Goal � ... � ... � Start with goal; ʻ undo ʼ actions until initial state � Plan-space search � Edges = inverse actions a " 1: � Result(a " 1 ,s) =s\ effects(a) ∪ precond(a) Large branching factor: many possible actions; not every Result(a " 1 , s) leads back to initial state � Searching plan-space � State space search is inefficient � Observation 1: many actions are independent. � States in plan-space are partial plans: = sets of partially instantiated actions with constraints on e.g.: move(A,B,C) and move(D,E,F) � We don ʼ t want to have to commit to specific order. � precedence and variable (in)equality � � move(A,B,x) < move(B,y,z); z # A Observation 2: naïve backward search requires fully instantiated actions. We often don ʼ t know/care Solution is (partially ordered) complete plan with fully how to instantiate variables. � instantiated actions � move(A,B,?C) is prerequisite for move(B,D,E) , but we don ʼ t � care which C A moves to. � � � CS440/ECE448: Intro AI � 15 � CS440/ECE448: Intro AI � 16 �
Searching plan-space � Flaws: open goals � Open goal: a precondition that is not yet met � 1. Start with the empty plan = {start state, goal state} move(A,B,x) requires clear(x) � � Solution : � 2. Iteratively refine current plan to resolve flaws � (refine = add new actions and constraints) add new action and precedence constraint: move(A,B,x) needs to be preceded by � some new action A with effect clear(x). � 3. Solution = a plan without flaws � � CS440/ECE448: Intro AI � 17 � CS440/ECE448: Intro AI � 18 � Flaws: threats � C is a threat if A is a precondition for B and C undoes the effect of A. � move(A,B,x) establishes precondition clear(B) for move SATplan � (C,D,B). move(E,F,B) undoes clear(B) � Solution: add new precedence constraint: move(E,F,B) has to precede move(A,B,x) , or follow move(C,D,B) . CS440/ECE448: Intro AI � 19 �
SATplan: basic idea � From plans to propositional logic � – Fluents are ground literals: We can encode a plan of fixed length n clear(B) t : block B is clear at time t (n time steps required for solution) � as a formula in propositional logic. � – Actions are ground implications: � ( preconditions t ∧ action t ) " effect t+1 There is a solution if this formula is satisfiable. Use existing tools (SAT solvers) � Operator move(x,y,z): � PRE: on(x,y), clr(z) EFFECT: on(x,z),clr(y) Action move(A,B,C) 23 If there is no solution of length n, try n+1. � ( on(A,B) 23 ∧ clr(C) 23 ∧ move(A,B,C) 23 ) $ on(A,C) 24 ∧ clr(B) 24 CS440/ECE448: Intro AI � 22 � Basic idea � 1. Create an easier, relaxed problem P ʼ : � – can be solved in polynomial time � – relax = remove some restrictions � Graphplan � – Solutions to P ʼ ⊃ solutions to P � 2. Solve this relaxed problem P ʼ� 3. Search among solutions to P ʼ for solutions to P � � Iterative deepening: try to solve P ʼ in 1,…,n steps �
Basic idea � Planning graph: nodes � Relaxed problem P ʼ : can we satisfy some Two kinds of levels alternate: � necessary precondition for the goal of P in k steps? State level S i : (N.B.: this only solves P if all necessary preconditions can be Node at level S i : a ground fluent (pos. or achieved in k steps) � neg. literal) which may hold i actions after S 0 � � � Solve P ʼ : build a planning graph of depth (2)k � � Action level A i : � Solve P: do backward search on the planning graph Node at level A i : a ground action (incl. noop ) to extract solution to P. If this fails, set k to k+1. � whose preconditions might be satisfied at S i � � CS440/ECE448: Intro AI � 26 � Preconditions/effects: Have your cake and eat it too! � edges between levels � Init: Have(Cake) From state level S i to action level A i : Goal: Have(Cake) ∧ Eaten(Cake) the node (fluent) at level S i is a precondition for the � node (action) at level A i Action Eat(Cake): � From action level A i to state level S i+1 � PRECOND: Have(Cake) the node (fluent) at level S i+1 is an effect EFFECT: ¬ Have(Cake) ∧ Eaten(Cake) of the node (action) at level A i � � Action Bake(Cake): S i A i S i+1 PRECOND: ¬ Have(Cake) Have(cake) Eat(cake) ¬Have(cake) EFFECT: Have(Cake) CS440/ECE448: Intro AI � 27 � CS440/ECE448: Intro AI � 28 �
Mutually exclusive actions: Persistence (no-op) actions � mutex links within action levels � – Inconsistent effects: For each literal C i at state level S i : � effect of A 1 negates effect of A 2 – add a persistence action Noop C eat(cake) negates bake(cake) at action level A i � � – Link from C i to Noop C � – Interference: – Also add C (i+1) to state level S i+1 � effect of A 1 negates precondition of A 2 – Link from Noop C to C i+1 � eat(cake) interferes with no-op for have(cake) � S i A i S i+1 – Competing needs: – Have(cake) Have(cake) preconditions of A 1 , A 2 are mutex � eat(cake) competes with bake(cake) � CS440/ECE448: Intro AI � 29 � CS440/ECE448: Intro AI � 30 � Mutually exclusive fluents: The initial planning graph � edges within state levels � Action Eat(Cake) Mutex within state level S i : F1 and F2 PC: Have(Cake) EF: ¬ Have(Cake) ∧ Eaten(Cake) cannot hold at the same time. � Action Bake(Cake ) PC.:¬ Have(Cake) EF: Have(Cake) – Negation: � S 0 A 0 S 1 have(Cake) negates ¬ have(Cake) � – Inconsistent support: Have ( Cake ) Have ( Cake ) all actions a1 to achieve F1 are mutex ¬ Have ( Cake ) with any action a2 that achieves F2. Eat(Cake) have(Cake) and eaten(Cake) � Eaten ( Cake ) ¬ Eaten ( Cake ) ¬ Eaten ( Cake ) CS440/ECE448: Intro AI � 31 � CS440/ECE448: Intro AI � 32 �
Recommend
More recommend