Interconnect Gate delay Wire delay The delay in VLSI circuits - PowerPoint PPT Presentation

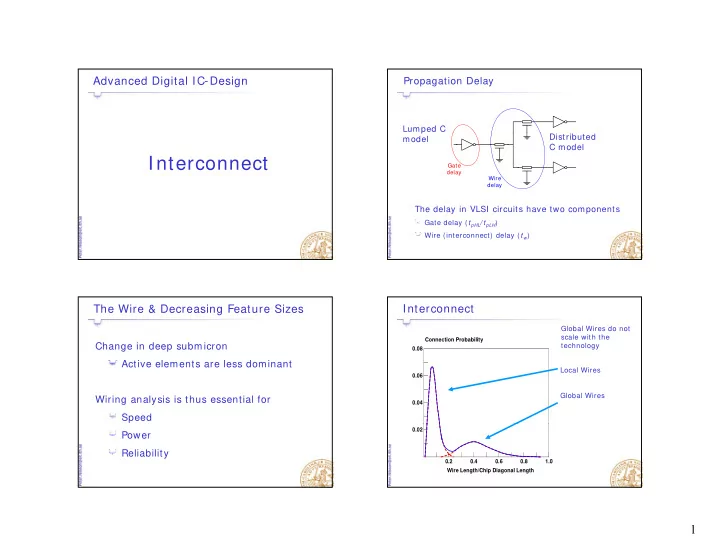
Advanced Digital IC-Design Propagation Delay Lumped C p Distributed model C model Interconnect Gate delay Wire delay The delay in VLSI circuits have two components Gate delay ( t pHL / t pLH ) Wire (interconnect) delay ( t w ) The Wire & Decreasing Feature Sizes Interconnect Global Wires do not scale with the Connection Probability Change in deep submicron technology 0.08 Active elements are less dominant A i l l d i Local Wires 0.06 Global Wires Wiring analysis is thus essential for 0.04 Speed 0.02 Power Reliability 0.2 0.4 0.6 0.8 1.0 Wire Length/Chip Diagonal Length 1

Wire Delay Dominates Today Wire Parasitics Mid 80: ties Wire 85% 15% Parasitic classes Mostly gate delay Capacitive Resistive Wire Inductive Mid 90: ties 50% 50% Gate delay and wire Substrate delay Reduces Performance Reduces Performance Increase Power Consumption Today 20% 80% Affect Reliability Mostly wire delay Reliability Problems Power Supply Noise V DD Power supply noise R Wire R Wire V DD V Cross talk - capacitive and inductive coupling Transmission line effect (ringing effect) I Switch V These effects will degrade the reliability in the digital system Resistive & inductive parasitics 2

Power Supply Noise Cross Talk V A voltage or a current Logic failure probability is accentuated when change may influence g y C Coupling C C scaling down the supply voltage li d th l lt li V V the signal on a parallel wire, especially on: Improvements Reduce wire resistance (copper, wider wires) Long wires I Sub micron technology Reduce pin inductance (good packages) Mutual Several metal layers y Inductance Inductance Stabilize power supply (on-chip decoupling) Stabilize power supply (on chip decoupling) I Capacitive and inductive coupling Long Wires are Sensitive Where Large silicon designs V V V V Ideal V/ 2 V/ 2 In global interconnects (System-on-Chip) V V/ 2 Degraded Especially in Mixed-Signal Design Ringing effect due to coupling of digital and analog signals inductance i d Possible logic error 3

Transmission Line Effect Transmission Line Effect Improvements Consider a 3 GHz Pentium Proper Impedance matching The wavelength is calculated by The wavelength is calculated by We have to be Avoid unnecessary long signal routing = × 8 c 3 10 m/s aware of the = f 3 GHz Design the transmission line as close transmission line × c 3 10 8 effects! λ = = = to ground as possible 0.1m × f 3 10 9 Buffering Buffering Transmission line effects are important at l ff λ 0.1m ≈ = = L 1 cm wire 10 10 Cross Talk Reduction Techniques Cross-Talk Example = × μ 2 Overlap 3 1 m Overlapping Widen the spacing between signal lines ≈ μ × μ = C 3 m 2 0.057 fF/ m 2 0.171fF wire plate V DD DD ≈ × μ × μ = C C 2 3 2 3 m 0.054 fF/ m 0 0 4 f / 0 324 f 0.324 fF C X fringing φ = C 0.5 fF x Route signals on different layers; Out = C 6 fF L C L In orthogonal to each other PDN φ A 2.5V transition give Minimize parallel run lengths between C 6 = = = V L V 2.5 2.3 V signals out + DD + C C 6 0.5 L X Capacitive voltage division 4

Cross Talk on a Bus Reducing Cross-Talk The cross coupling C have double swing Shielding Wire Bus Bus GND GND Avoid parallel wires Shielding V DD Shielding Layer GND Miller effect increase the cross talk Substrate Swizzled Bus Routing Interleaved Busses Busses with different switching time Switch the bit order every turn Reduces the coupling Reduces the coupling educes t e coup g Reduces noise Reduces noise 1 3 2 7 0 2 4 6 1 3 5 7 5 6 0 4 0 2 4 6 0 2 4 6 1 3 5 7 1 3 5 7 Source: Intel Source: Intel 5

Metal Layers Capacitance: Parallel Plate SiO SiO 2 L ε WL W = C ox H t Metal/Poly etc. ox t t ox Substrate A 3D Problem! − = × 15 ε 3.5 10 F cm / for SiO ox 2 Capacitance: Fringing Metal Layers Contacts (via) H Metal W Note W W H H the Size! Fringing C 6

Impact of Fringing Capacitance Wire Resistance Sheet Resistance 6 Capacitance pF/cm Fringing ρ L L = × = × R R capacitance R R W H W dominates for H/t ox =1 small W/ t ox R 1 0.35 μ ≈ H/t ox =0.5 R R W W=H=t ox C plate R L R R R R H H W R R R t ox 0.1 H R Metal/Poly etc. 0.1 0.4 1 4 10 W/t ox Silicide Using Bypasses (e.g. in memories) Silicide to reduce the poly resistance Driving a word line from both sides Driver Silicide Polysilicon word line Polysilicon SiO 2 Metal word line n + n + p - Using a metal bypass Using a metal bypass Polysilicon word line Advanced technologies have silicide on poly Metal bypass 7

Repeaters Reduce Delay The Elmore Delay = + + + + + + + + + τ R C (R R )C (R R R )C (R R R R )C � RC increases quadratically with the length 1 1 1 2 2 1 2 3 3 1 2 3 4 4 Driver R 1 R 2 R 3 R 4 R 5 R 6 Wire C 1 C 2 C 3 C 4 C 5 C 6 Idea: With repeaters The resistance from source to node 3 is R 1 + R 2 + R 3 . That resistance should thus be used to load C 3 Distributed RC-Line RC-Models R R Distributed Distributed Lumped Lumped C C Lum ped Distributed RC-line Model t p (0 -> 50% ) 0.69 RC 0.38 RC RC (0 -> 63% ) RC 0.5 RC r Δ L t r (10% -> 90% ) 2.2 RC 0.9 RC r Δ L r Δ L Distributed c Δ L c Δ L c Δ L c Δ L c Δ L c Δ L Model Lumped model tends to be pessimistic L 8

Lumped Model (Elmore Delay) Distributed Model (Elmore Delay) 3.19 ns when the − = Ω = Ω − = Ω = Ω R 1300 ; R 1000 R 1300 ; R 1000 lumped model was eq p wire eq p wire = = = = = = C 0.2 pF ; C 1.1 pF ; C 0.8 pf C 0.2 pF ; C 1.1 pF ; C 0.8 pf used int wire L int wire L = × + = × + t 0. 6 9 R C − t 0.69 R C − t = 0.69 1300 0.2 1 × × × 0 1 2 + t = 0.69 1300 0.2 10 × × × 1 2 + − − p L H eq p i nt pH L eq p in t pHL pHL + × + × + + × + × × + 0. 6 9 ( R R ) C (0.69 R 0.38 R ) C + × + × × − 12 + + × + × × × − 12 + 0.69 (1300 1000) 1. 1 10 (0.69 1300 0.38 1000) 1.1 1 0 eq p − wire wire eq p − wire wire + × + × + × + × 0.69 ( R R ) C 0 .69 ( R R ) C + × + × × − 12 = + × + × × − 12 = 0.6 9 (1300 1000) 0 . 8 1 0 0 .69 (1300 1000) 0.8 1 0 − − eq p w ire L eq p w i re L = = 3.1 9 ns 2. 8 5 ns R eq-p R eq-p 10 m m long wire 10 m m long wire R eq-n C int C L R eq-n C int C L Driving a Large Fan-Out Driving Large Capacitances Driving a large R eq C int = Intrinsic capacitance Typical examples: capacitance C ext = Extrinsic capacitance Busses R eq = Resistance in channel Clock network C int = C db +C gd = + Control wires (e.g. set and reset signals) C C C ext w g Memories (driving a large number of storage cells) C w = Wire capacitance R eq C g = Gate C in next stage V DD V DD DD Worst case: R eq Off chip signals C L R eq C int C ext 9

Scaling to increase driving capability Scaling to Increase Driving Capability R eq Scaling W with a factor S : Delay RC-model C = + + = + + t t 0.69 0.69 R R ( ( C C C C ) ) 0.69 0.69 R C R C (1 (1 ext ) ) = × C S C p p eq eq int int ext ext eq eq int int C int int iref C int = C db +C gd Scaling with a factor S R = ref R R C C eq = ref + = + S t 0.69 S C (1 ext ) t (1 ext ) p iref p 0 S S C S C R eq iref iref V DD DD t p 0 = intrinsic delay R eq Independent of S R eq C int C ext Scaling Example Scaling Example (p206) 1 = × + = = = t 19.3 (1 ) ps t 19.3 ps ; C 3.15 fF ; C 3.0 fF p 0 ext iref p × 1.05 S C 1 = + + = + + t t t t 0 (1 (1 ext ext ) ) 19.3 (1 19 3 (1 ) ) ps p p × S C 1.05 S iref t p (ps) S = 5, Substantial improvement 40 S > 10, ”No more gain” 30 C iref C C ext C 20 10 S 0 5 10 15 10

Sizing a Chain of Inverters Sizing a Chain of Inverters Scale factor optimum is Each stage is scaled with Each stage is scaled with the same factor f γ + (1 ) = f f e 1 2 N 1 1 2 2 N N C g, 1 C int, 1 C g, 2 C int, 2 C g, N C int, N C g, N+1 = C L C g, 1 C int, 1 C g, 2 C int, 2 C g, N C int, N C g, N+1 = C L Sizing a Chain of Inverters Sizing a Chain of Inverters γ Too many stages + t (1 ) Has no closed form p Normalized delay = f f f e solution except for γ = 0 o γ t popt so u o p 0 6 6 Common γ = 0 when intrinsic capacitance is neglected Practice 4 Around 4 = Otherwise: f is f e solved numerically 2 1 2 N 1 (1 + ) f = f e f for C g, 1 C int, 1 C g, 2 C int, 2 C g, N C int, N C g, N+1 = C L 1 2 3 4 5 11