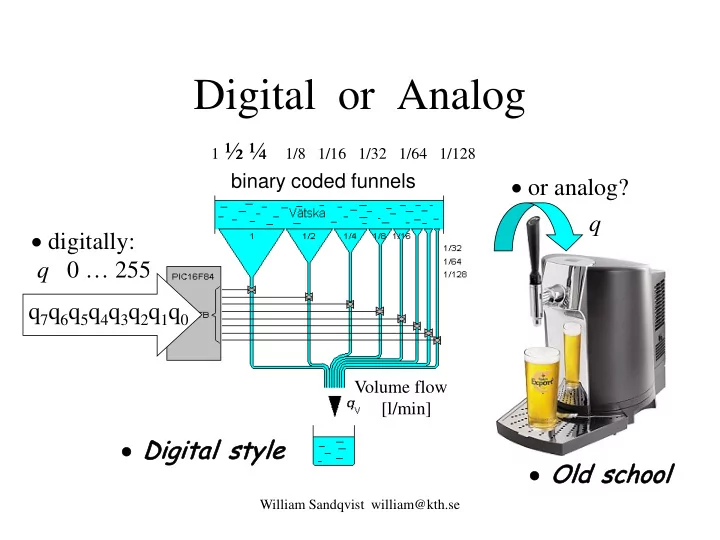

Digital or Analog 1 ½ ¼ 1/8 1/16 1/32 1/64 1/128 • or analog? binary coded funnels q • digitally: q 0 … 255 q 7 q 6 q 5 q 4 q 3 q 2 q 1 q 0 Volume flow [l/min] • Digi gita tal s sty tyle • Old sc d school William Sandqvist william@kth.se
Digital → Analog converter? • Binary coded resistor values b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 U U = = DA converter I 1 R 1 1 1 + + + ... R R R 1 2 n b b b b = ⋅ + + + + 0 1 2 7 5 ... 100000 50000 25000 781 The current I is the sum of the currents from the ”binary coded” 1 ½ ¼ 1/8 1/16 1/32 1/64 1/128 × 100 k Ω resistors. William Sandqvist william@kth.se
Digital → Analog converter? DA converter b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 256 steps 0,5 µ A/step U b b b b b b b b = = ⋅ + + + + + + + 0 1 2 3 4 5 6 7 5 I 100000 50000 25000 12500 6250 3125 1563 781 R 1 1 1 1 1 1 1 1 = ⋅ + + + + + + + = µ 5 128 A I max 100000 50000 25000 12500 6250 3125 1563 781 William Sandqvist william@kth.se
Problems with tolerances Binary coded resistors for 8 bit. Biggest resistor exactly 100000 Ω and smallest resistor exactly 781 Ω (preferably 781,25 )? It is difficult to manufacture such various resistors with tight tolerances. • There is a better solution! R2R - method. William Sandqvist william@kth.se
R-2R-ladder b 4 b 3 b 2 b 1 b 0 b 0 b 1 b 2 b 3 b 4 Just one resistance value needs to be manufactured, R, and then R + R =2 R . One must be able to produce many "equal" resistors - the exact value is no longer important. William Sandqvist william@kth.se
Two-terminal equivalent R I The R2R-ladder is not that easy to understand … Repeated use of two-terminal equivalents and the superposition rule is what is required. William Sandqvist william@kth.se
R-2R b 0 =0 R I =? b 0 ⋅ 2 2 = = = Ω ? 1 k R R + I I 2 2 William Sandqvist william@kth.se
R-2R b 0 =1 R I =? b 0 ⋅ 2 2 = = = Ω ? 1 k R R + I I 2 2 b 0 1 or 0, same internal resistance! William Sandqvist william@kth.se
R-2R b 0 R I =? b 0 = + = Ω 1 1 2 k R I The total resistance of one stage becomes 2 k Ω . William Sandqvist william@kth.se
R-2R b 1 =0 R I =? =2 k Ω b 1 = ? R I ⋅ 2 2 = = Ω 1 k R + I 2 2 William Sandqvist william@kth.se
R-2R b 1 =1 R I =? =2 k Ω b 1 = ? R I ⋅ 2 2 = = Ω 1 k R + I 2 2 b 1 1 or 0, same internal resistance! William Sandqvist william@kth.se
R-2R b 1 R I =? =2 k Ω • Conclusion: b 0 b 1 = + = Ω 1 1 2 k R I Regardless 1’s or 0’s is the total input resistance from the previous stages always 2 k Ω William Sandqvist william@kth.se
Two-terminal equivalent E 0 William Sandqvist william@kth.se
R-2R b 4 =1 E 0 =? =2 k Ω + b 0 b 1 b 2 b 3 b 4 E 0 − William Sandqvist william@kth.se
R-2R b 4 =1 E 0 =? Volage divider: =2 k Ω + b 4 E 2 E 0 = = E E − + 0 2 2 2 William Sandqvist william@kth.se
R-2R b 3 =1 E 0 =? =2 k Ω + b 0 b 1 b 2 b 3 b 4 E 0 − William Sandqvist william@kth.se
R-2R b 3 =1 E 0 =? ⋅ 2 2 = Ω 1 k + 2 2 + 2 k Ω + E 0 − b 3 E 0 2 E = − E + 2 2 2 + E E = E 0 4 2 − William Sandqvist william@kth.se
R-2R conclusion E 0 … + b 0 b 1 b 2 b 3 b 4 E 0 − E E E = ⇒ = ⇒ = ⇒ 1 1 1 ... b b b 4 3 2 2 4 8 • Reasonable guess – is it not? William Sandqvist william@kth.se
R-2R superposition + b 0 b 1 b 2 b 3 b 4 E 0 − • According to the superposition principle, the contributions of b 4 b 3 b 2 … b 0 can be added individually: We have a b b b b b = ⋅ + + + + 4 3 2 1 0 b 4 b 3 b 2 b 1 b 0 DA-converter! E E 0 2 4 8 16 32 William Sandqvist william@kth.se
R-2R simulation b 3 b 2 b 0 b 1 b 3 b 2 b 1 b 0 =1010 Guess value of voltage OUT? William Sandqvist william@kth.se
William Sandqvist william@kth.se
AD-converter? William Sandqvist william@kth.se
Successive approximations Analog ”Comparator” Guess! AD-converter contains a DA- Digitally converter , and an analog voltage comparator. AD conversion according to the method of successive approximations is comparable to weigh an unknown mass with binary weights on a balance. We try step by step to adding binary ”weight” if ” < ” or remove ” weight” if ” > ” . William Sandqvist william@kth.se
Binary weights 8 4 2 1 … 8 8+4 AD conversion takes time. For each bit 8+2 higher resolution a comparison one step further is required. 8+2+1 William Sandqvist william@kth.se
An AD-converter, 14 channels AD converter occupies a large area on the chip - so it is economic to use the same converter to alternately measure up to 14 different sources, channels. The PIC- processor has a 10-bits AD- Channel selection multiplexor. converter William Sandqvist william@kth.se
Supply voltage as reference It is easiest to use the supply voltage as ADC comparison value – reference . The drawback is that it is not particularly accurate. William Sandqvist william@kth.se
Internal or external reference? Why external reference? William Sandqvist william@kth.se
Stabilized reference 4,096 V MCP1541 If you buy a stabilized reference circuit you can perhaps choose the value 4,096 V ( 4096=2 12 ) which gives a 10-bit AD- converter exact 4 mV-steps, without the need to scale the measured result with multiplications and divisions. William Sandqvist william@kth.se
Ratiometric connection Same voltage! sensor If a sensor measurement value depends on it’s supply voltage, you can either have stabilized supply (expensive) – or easier, use so-called ratiometric connection. If the sensor supply voltage and AD converter reference voltage are the same , then changes in this voltage will be the same for both, and the AD converted measured value will remain intact! William Sandqvist william@kth.se
Adapt measuring range An NTC thermistor has a high sensitivity but a non-linear temperature relationship. One linearize with a resistor – and then get the measuring range 0 …3,5 V. If the reference is 3,5 V instead of 5 V then one utilizes the entire ADC range for the measurement. William Sandqvist william@kth.se
Are 10-bit resolution required? b 9 b 8 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 AD converter is 10 bits. What does a sensor cost 10 bits that has 10-bit resolution? 1024 steps 100 $ ? 5 mV/step resolution ≈ 0,1% More common is that you can afford an 8-bit sensor. ( PIC processor itself costs 2 $ ). The picture shows a resistive position sensor that can take advantage of 10-bit resolution. William Sandqvist william@kth.se
8-bit program If one need only 8 bit resolution one can ignore the two least significant bits and handle the result as a byte. b 9 b 8 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 8 bit 256 steps 20 mV/step resolution ≈ 1% William Sandqvist william@kth.se
8-bit program 0 One can care only about the 8 most significant bits! 0 ADFM=0; char value; value = ADRESH; /* 8-bit measurement */ William Sandqvist william@kth.se
Avoid amplifier If one only need 8 bit resolution one can still use the 10-bit resolution to avoid the need to amplify the sensor signal, the two most significant bits becomes constant. One can therefore ignore to read them. 1 0 b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 43 ° A fever thermometer only 8 effective bits, need a small temperature 34 ° 256 effective steps range 34 ° …43 ° with 5 mV/step (right?) resolution ≈ 1% William Sandqvist william@kth.se
8-bit program (10 bit) One can care only 1 about the 8 least significant bits that change! 1 ADFM=0; char value; value = ADRESL; /* 8-bit measurement */ William Sandqvist william@kth.se
16-bit program 10-bits When you really need 1024 steps 1 10 bits in a 16-bit 5 mV/step variable. resolution ≈ 0,1% 1 ADFM=1; unsigned long value; value = ADRESH * 256; value += ADRESL; /* 10-bit measurement */ William Sandqvist william@kth.se
William Sandqvist william@kth.se
What happens if the signal changes during conversion? The result is a value that has occurred during the AD converter can conversion, but at not "undo" a an unspecified time! previously determined bit! William Sandqvist william@kth.se
The problem The time for the sampling is indeterminate! William Sandqvist william@kth.se
Sample & Hold - circuit The solution is that the analog signal is "frozen" during the conversion. At the AD conversion start a switch is taking a "sample" of the signal and stores it in a capacitor. The course PIC processor, the sampling capacitor has capacitance ≈ 10pF. William Sandqvist william@kth.se
Acquisition time t ACQ Every time one has chosen/changed channel the sampling capacitor C HOLD must have time to recharge to the analog voltage. This will take about 5 µ s. A 5 µ s delay can simply be programmed as: nop2(); nop2(); nop(); /* 5 us 4 MHz clock */; William Sandqvist william@kth.se
Recommend
More recommend