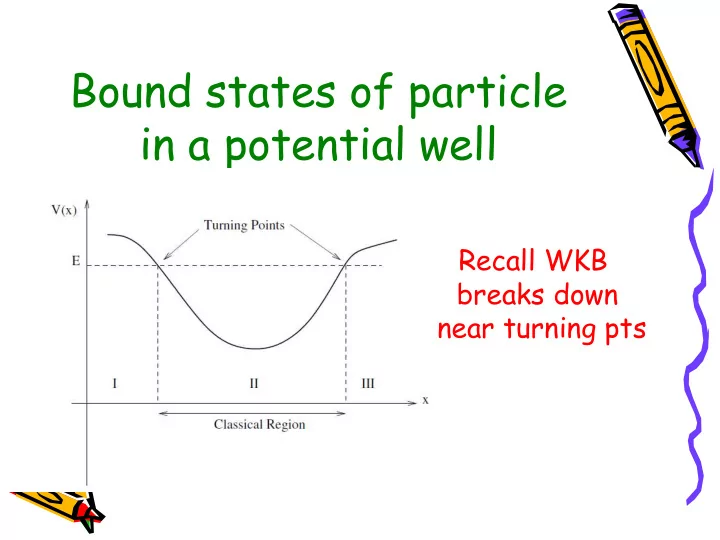
Bound states of particle in a potential well Recall WKB breaks - PowerPoint PPT Presentation

Bound states of particle in a potential well Recall WKB breaks down near turning pts

These must be smoothly connected across turning points For that, we expand the potential near turning points Substitute in Schrodinger equation near turning points

Similarly near x=x 2 Define variable z as follows

Equation to solve Solutions are Airy functions Fourier transform Inverse Fourier transform

solution prove We are interested in asymptotic form of Airy function to fix constants C 1 , C 3 in region I and III solution

Asymptotic form Region I C 1 can be fixed by comparing z>>0 Airy function asymptotic form

Region II • General solution can be written with a phase shift as follows: • Near x=x 1

C 2 = 2 C 1 , a = p/4 Do a similar exercise near x= x 2 Region II, x < x 2 and z <<0 and region III z>>0 Region III

In region II

Asymptotic Airy function comparison with WKB wavefunction near x=x 2 Wavefunction in region II obtained near x=x 1 and x=x 2 must be same. This will fix relation between C 1 , C 3

Compare with the form C 1 = (-1) n C 3 Solution agrees if

connection formula for potential barrier • This will be useful to work out the transmission coefficient T for a barrier. • Please work out connection formula - In region I and III, E> V and in region II we will have E<V. • Oscillatory in region I and III but exponential in region II • For high and broad barrier what is T

Using connection formula, try to derive where Transmission coefft For high and broad barrier θ >>1

Lifetime τ of parent nucleus from α lpha decay • τ is inversely proportional to T • Assignment problems