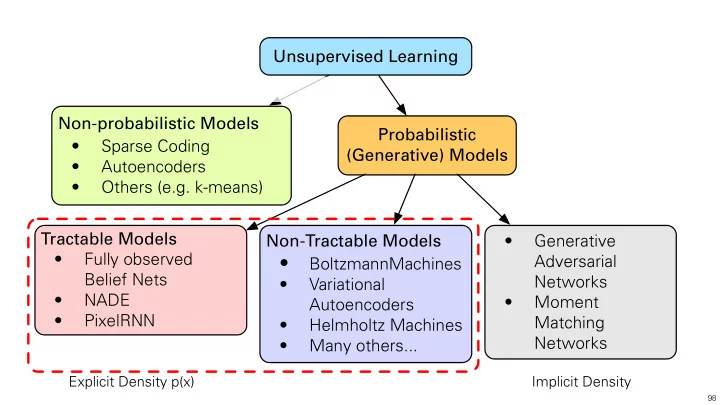

Unsupervised Learning Non-probabilistic Models Probabilistic • Sparse Coding (Generative) Models • Autoencoders • Others (e.g. k-means) Tractable Models Non-Tractable Models • Generative • Fully observed • Adversarial BoltzmannMachines Belief Nets Networks • Variational • NADE • Moment Autoencoders • PixelRNN Matching • Helmholtz Machines Networks • Many others... Explicit Density p(x) Implicit Density 98
Unsupervised Learning • Basic Building Blocks: • Sparse Coding • Autoencoders • Deep Generative Models • Restricted Boltzmann Machines • Deep Boltzmann Machines • Deep Belief Networks • Helmholtz Machines / Variational Autoencoders • Generative Adversarial Networks 99
Deep Generative Model Sanskrit Sanskrit Model P(image) 25,000 characters from 50 alphabets around the world. • 3,000 hidden variables • 784 observed variables (28 x 28 images) • About 2 million parameters Bernoulli Markov Random Field 100
Deep Generative Model Conditional Simulation Why so difficult? 28 28 28 28 p possible images! P(image | partial image) Bernoulli Markov Random Field 101
Fully Observed Models • Explicitly model conditional probabilities: n Y p model ( x ) = p model ( x 1 ) p model ( x i | x 1 , . . . , x i − 1 ) i =2 Each condiAonal can be a 102
Fully Observed Models • Explicitly model conditional probabilities: n Y p model ( x ) = p model ( x 1 ) p model ( x i | x 1 , . . . , x i − 1 ) i =2 Each conditional can be Each condiAonal can be a a complicated neural network 103
Fully Observed Models • Explicitly model conditional probabilities: n Y p model ( x ) = p model ( x 1 ) p model ( x i | x 1 , . . . , x i − 1 ) i =2 Each conditional can be Each condiAonal can be a a complicated neural network • A number of successful models, including ⎯ NADE, RNADE (Larochelle, et.al. 2011) ⎯ Pixel CNN (van den Ord et. al. 2016) ⎯ Pixel RNN (van den Ord et. al. 2016) Pixel CNN Pixel CNN 104
Restricted Boltzman Machines Feature Detectors Graphical Models: hidden variables Powerful framework hidden variables for representing dependency structure between random variables Image visible variables image visible variables RBM is a Markov Random Field with: es • Stochastic binary visible variables les • Stochastic binary hidden variables • Bipartite connections. Markov random fields, Boltzmann machines, log-linear models. 105
Restricted Boltzman Machines Feature Detectors Pairwise Unary hidden variables hidden variables Partition function (intractable) Image visible variables image visible variables RBM is a Markov Random Field with: es • Stochastic binary visible variables les • Stochastic binary hidden variables • Bipartite connections. Markov random fields, Boltzmann machines, log-linear models. 106
Restricted Boltzman Machines Feature Detectors Pairwise Unary hidden variables hidden variables Image visible variables image visible variables RBM is a Markov Random Field with: es • Stochastic binary visible variables les • Stochastic binary hidden variables • Bipartite connections. Markov random fields, Boltzmann machines, log-linear models. 107
Learning Features Learned W: “edges” Observed Data Subset of 1000 features Subset of 25,000 characters Subset of 1000 features Subset of 25,000 characters Sparse New Image: New Image: representations …. = LogisAc FuncAon: Suitable for Logistic Functon: Suitable for modeling binary images modeling binary images 108
Model Learning Hidden units Hidden units Given a set of i.i.d. training , Given a set of i.i.d. training examples model parameters we want to learn rs . Max Image visible units image visible variables 109
Model Learning Hidden units Hidden units Given a set of i.i.d. training , Given a set of i.i.d. training examples model parameters we want to learn rs . Maximize log-likelihood objective: Max Image visible units image visible variables 110
Model Learning Hidden units Hidden units Given a set of i.i.d. training , Given a set of i.i.d. training examples model parameters we want to learn rs . Maximize log-likelihood objective: Max Image visible units image visible variables DerivaAve of the log-likelihood: Derivative of the log-likelihood: 111
Model Learning Hidden units Hidden units Given a set of i.i.d. training , Given a set of i.i.d. training examples model parameters we want to learn rs . Maximize log-likelihood objective: Max Image visible units image visible variables DerivaAve of the log-likelihood: Derivative of the log-likelihood: Difficult to compute: exponenAally many configuraAons 112
Model Learning Hidden units Hidden units Given a set of i.i.d. training , Given a set of i.i.d. training examples model parameters we want to learn rs . Maximize log-likelihood objective: Max Image visible units image visible variables DerivaAve of the log-likelihood: Derivative of the log-likelihood: Difficult to compute: Exponentially many Difficult to compute: exponenAally many configuraAons configurations 113
Model Learning Hidden units Hidden units Derivative of the log-likelihood: Max Image visible units image visible variables Easy to Easy to compute compute exactly exactly Difficult to compute: Difficult to compute: Exponentially many configurations Use MCMC Approximate maximum like kelihood learning 114
Approximate Learning • An approximation to the gradient of the log-likelihood objective: ace the average over all possible input configuraAons by s • Replace the average over all possible input configurations by samples • Run MCMC chain (Gibbs sampling) starting from the observed examples. • Initialize v 0 = v • Sample h 0 from P(h | v 0 ) • For t=1:T ⎯ Sample v t from P(v | h t-1 ) ⎯ Sample h t from P(h | v t ) 115
Approximate ML Learning for RBMs • Run Markov chain (alternating Gibbs Sampling): 116
Approximate ML Learning for RBMs • Run Markov chain (alternating Gibbs Sampling): Data Data 117
Approximate ML Learning for RBMs • Run Markov chain (alternating Gibbs Sampling): Data Data D 118
Approximate ML Learning for RBMs • Run Markov chain (alternating Gibbs Sampling): … Data T=1 Data T=1 D 119
Approximate ML Learning for RBMs • Run Markov chain (alternating Gibbs Sampling): … Data T=1 Data T=1 T= infinity T=infinity D Equilibrium Equilibr Distribution D 120
Contrastive Divergence • A quick way to learn RBM: • Start with a training vector on the visible units. • Update all the hidden units in parallel. • Update the all the visible units in parallel to get a “reconstruction”. • Update the hidden units again. Data Reconstructed Data Data Reconstructed Data • Update model parameters: • Implementation: ~10 lines of Matlab code. (Hinton, Neural Computation 2002) 121
Contrastive Divergence • A quick way to learn RBM: • Start with a training vector on the visible units. • Update all the hidden units in parallel. • Update the all the visible units in parallel to get a “reconstruction”. • Update the hidden units again. Data Reconstructed Data Data Reconstructed Data The distributions of data and reconstructed data should be the same. • Update model parameters: • Implementation: ~10 lines of Matlab code. (Hinton, Neural Computation 2002) 122
RBMs for Real-valued Data Hidden units Hidden units Pairwise Unary Max image visible variables Image visible units Gaussian-Bernoulli RBM: • Stochastic real-valued visible variables • Stochastic binary hidden variables • Bipartite connections. 123
RBMs for Real-valued Data Hidden units Hidden units Pairwise Unary Max image visible variables Image visible units 4 million unlabelled images 4 million unlabeled images unlabeled Learned features (out of 10,000) 124
RBMs for Real-valued Data 4 million unlabelled images 4 million unlabeled images unlabeled Learned features (out of 10,000) = 0.9 * + 0.8 * + 0.6 * … New Image New Image 125
RBMs for Word Counts Unary Pair-wise Pairwise Unary 0 1 D K F D K F 1 X X X X X X W k ij v k v k i b k P θ ( v , h ) = Z ( θ ) exp i h j + i + h j a j 0 @ A i =1 j =1 i =1 j =1 k =1 k =1 0 0 1 ⇣ ⌘ i + P F b k j =1 h j W k exp ij 0 P θ ( v k i = 1 | h ) = ⇣ ⌘ P K b q i + P F j =1 h j W q q =1 exp ij Replicated Softmax Model: undirected topic model: • Stochastic 1-of-K visible variables. • Stochastic binary hidden variables • Bipartite connections. (Salakhutdinov & Hinton, NIPS 2010, Srivastava & Salakhutdinov, NIPS 2012) 126
RBMs for Word Counts Unary Pair-wise Pairwise Unary 0 1 D K F D K F 1 X X X X X X W k ij v k v k i b k P θ ( v , h ) = Z ( θ ) exp i h j + i + h j a j 0 @ A i =1 j =1 i =1 j =1 k =1 k =1 0 0 1 ⇣ ⌘ i + P F b k j =1 h j W k exp ij 0 P θ ( v k i = 1 | h ) = ⇣ ⌘ P K b q i + P F j =1 h j W q q =1 exp ij Replicated Softmax Model: undirected topic model: • Stochastic 1-of-K visible variables. • Stochastic binary hidden variables • Bipartite connections. (Salakhutdinov & Hinton, NIPS 2010, Srivastava & Salakhutdinov, NIPS 2012) 127
Recommend
More recommend