
A new window on primordial non-Gaussianity based on 1201.5375 with M. Zaldarriaga Enrico Pajer Princeton University 2.0 � R � k � 2 � 10 9 1.5 Μ CMB � LSS 1.0 10 � 4 0.01 1 100 10 4 k Mpc
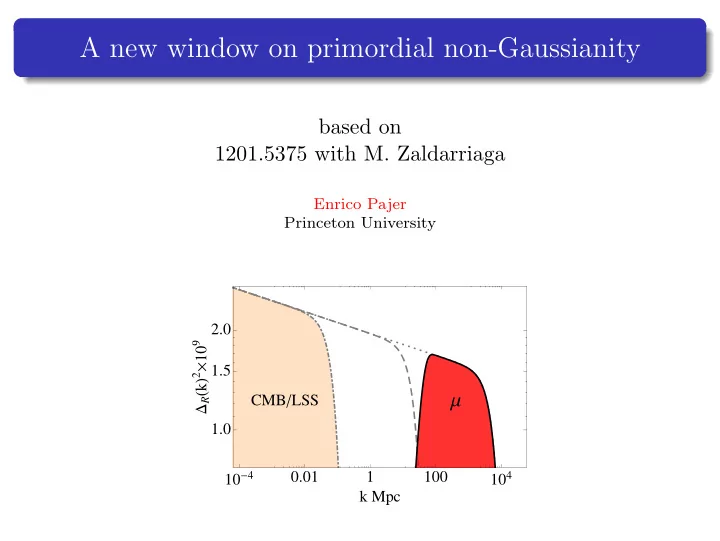
Summary We know little about primordial perturbations outside the range 10 − 4 � k Mpc � 1 µ -type spectral distortion of the CMB is a unique probe of small scales 50 � k Mpc � 10 4 [Sunyaev, Zel’dovich, Silk, Peebles, Hu, Danese, de Zotti, Chluba, . . . ] The monopole � µ (ˆ n ) � probes the small-scale power spectrum µT cross correlation probes the primordial bispectrum in the squeezed limit f loc NL Fisher forecast with current technology ∆ f loc NL � 10 3 Beat cosmic variance with an enormous number of modes Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 2 / 26
Outline 1 Motivations 2 Review of µ -distortion 3 A new window on primordial non-Gaussianity 4 Remarks Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 3 / 26
The golden age of cosmology We are living in the golden age of observational cosmology: COBE goes to Stockholm, WMAP, ACT & SPT measured the CMB with 1% accuracy. now Planck and a horde of ground and ballon based experiments Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 4 / 26
Primordial perturbations 1 H ? radiation matter dark E Log a Primordial superhorizon perturbations seed the structures in our universe They teach us about the earlier stage Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 5 / 26
The non-linear regime of structure formation Small superhorizon primordial perturbations → linear evolution Homogeneous background → no mix of different scales Perturbations re-enter the horizon → grow with time Large perturbations evolve in a complicated non-linear way → erase primordial information Linear regime: Large scale structures k < O (Mpc − 1 ) or look back in time Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 6 / 26
The cosmic microwave background A snapshot of the universe at 370 , 000 years, z ≃ 1100 Small perturbations δρ/ρ ∼ 10 − 5 → linearly related to primordial perturbations For l � 2000 or k > O (0 . 2 Mpc − 1 ) erased by diffusing damping! Can we access smaller scales? Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 7 / 26
The CMB/LSS window 2.00 1.00 0.50 outside CMB � LSS � R � k � 2 � 10 9 0.20 ? horizon Gaussian 0.10 0.05 Scale � inv 0.02 10 � 7 10 � 5 0.001 0.1 10 1000 k Mpc k � 10 − 4 Mpc − 1 are still outside our horizon k � 0 . 2 Mpc − 1 ( l � 2000) have been erased by Silk damping k � O (1) Mpc − 1 are now contaminated by gravitational non-linearities Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 8 / 26
Outline 1 Motivations 2 Review of µ -distortion 3 A new window on primordial non-Gaussianity 4 Remarks Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 9 / 26
The µ -era Before z i ≃ 2 × 10 6 double Compton scattering ( e − + γ → e − + 2 γ ) is very efficient. Perfect thermodynamical equilibrium, Planck spectrum n ( ν ) = ( e ν/k B T − 1) − 1 Between z i and z f ∼ 5 × 10 4 only elastic Compton scattering ( e − + γ → e − + γ ) is efficient. Photon number (almost) conserved. Bose-Einstein spectrum with chemical potential µ 1 n ( ν ) = e ν/k B T + µ − 1 After z f also elastic Compton scattering is not efficient, e.g. y -type distortion. Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 10 / 26
µ -distorted spectrum For µ > 0 the spectrum ν 2 n ( ν ) = e ν/k B T + µ − 1 looks like n � Ν � Ν � kT 0.5 1.0 2.0 5.0 Distinctive ν dependence. Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 11 / 26
Perturbations during the µ -era Perturbations during the µ -era 5 × 10 4 � z � 2 × 10 6 Dissipation of acoustic modes due to diffusion damping [Silk ’72] . Scale invariant power spectrum n s ∼ 1 µ ≃ 2 . 4 × 10 − 8 Adiabatic cooling → Bose-Eistein condensation [Khatri, Chluba Sunyaev ’11,’12] µ BE ≃ − 3 × 10 − 9 Non-standard physics e.g. decays of massive particles, . . . Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 12 / 26
Dissipation of acoustic modes Perturbations of the adiabatic mode R re-enter the horizon, oscillate and dissipate δ γ ∼ R k cos( kt ) e − k 2 /k 2 D Shear viscosity and heat conduction damp the oscillations [Silk, Kaiser, Weinberg] k D ≃ z 3 / 2 4 × 10 − 6 Mpc − 1 Now we can only see � R � k � 2 � 10 9 k < k D ( z L ) ≃ 0 . 2 × Mpc − 1 z L z f 1 z i 1 µ -distortion can see 50 < k Mpc − 1 < 10 4 10 � 4 0.01 1 100 10 4 k Mpc Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 13 / 26
Power dissipated in the µ era Analytical estimate of µ [Hu et al. 94’, Khatri Chluba & Sunyaev ’11] Energy in acoustic waves with relativistic correction i c 2 � s � δ 2 � δE ∼ ρ γ � � 1 + c 2 � s f Bose-Einstein spectrum with E → E + δE and fixed N µ ≃ 1 . 4 δE > 0 Linear integral probe of the z i � R � k � 2 � 10 9 power spectrum z L z f 1 1 Μ � d log k ∆ 2 µ ∝ R ( k ) 10 � 4 0.01 1 100 10 4 k Mpc Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 14 / 26
� µ (ˆ n ) � constraints the small-scale power spectrum The averaged µ -distortion over the whole sky (monopole) [Hu et al. ’94, Khatri Chluba Sunyaev ’11’12] � µ ( x ) � ≃ 9 � � i � e − 2 k 2 /k 2 d log k ∆ 2 R ( k ) f , D 4 Integral measure of the power spectrum at small scales For n s = 1 µ ∼ 2 × 10 − 8 Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 15 / 26
Relating µ to R 2 at small scales Dissipation is smeared over a volume k − 3 s Nature takes the average for us Small cosmic variance! [EP & Zaldarriaga ’12] Final analytical estimate � d 3 k 1 d 3 k 2 9 � k + � k 2 ) e i� R ( � k 1 ) R ( � k + · � x W µ ( x ) ≃ (2 π ) 6 2 k s � i � e − ( k 2 1 + k 2 2 ) /k 2 ×� cos ( k 1 t ) cos ( k 2 t ) � p D f Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 16 / 26
Outline 1 Motivations 2 Review of µ -distortion 3 A new window on primordial non-Gaussianity 4 Remarks Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 17 / 26
Primordial non-Gaussianity For a Gaussian random variable � δ 2 n +1 � = 0 , � δ 2 n � ∝ � δ 2 � n Using rotational and translational invariance �R 3 � ≡ (2 π ) 3 f NL F ( k 1 , k 2 , k 3 ) δ 3 ( k 1 + k 2 + k 3 ) Scale invariance: only k 1 /k 3 and k 2 /k 3 f NL gives the size F ( k 1 , k 2 , k 3 ) (normalized) gives the shape. Out[1320]= Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 18 / 26
Squeezed limit Squeezed limit k 3 ≪ k 1 ∼ k 2 . Short-scale power modulated by long scales � � 1 � � > 3 � 3 , 2 � k S � k S � k S k L ≪ k S �R ( k S ) 2 R ( k L ) � ∼ 1 lim A + B + C k 6 k L k L k L S Microphysical inflationary models: A � = 0 ⇒ instability B � = 0 ⇒ multi-field (more than one clock), e.g. curvaton, quasi-single-field, local template [Maldacena ’02, Creminelli Zaldarriaga ’04] C � = 0 ⇒ single or multi-field, e.g. small speed of sound, equilateral template Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 19 / 26
Local non-Gaussianity Local model peaks in the squeezed limit k 3 ≪ k 1 ∼ k 2 Distinguishes between broad classes of models �R ( k 1 ) R ( k 2 ) R ( k 3 ) � ∼ ∆ 2 ∆ 2 R R + 2perm ′ s k 3 k 3 1 2 Local in position space, e.g. [Komatsu Spergel ’01] R G ( x ) 2 − �R G ( x ) 2 � R ( x ) = R G ( x ) + f loc � � NL Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 20 / 26
µT cross correlation Μ � y � Μ � x � µ ∼ R 2 and T ∼ R µT ∼ R 3 ⇒ µT probe the primordial bispectrum in the squeezed limit f loc NL Straightforward computation 50 ∆ 4 NL b ≃ 3 × 10 − 16 R ( k p ) � µT � ∼ C µT l ( l + 1) f loc l ( l + 1) f loc ≃ NL b l b ∼ ∆ 2 R ( k D ) / ∆ 2 R ( k p ), if scale invariant b ∼ 1. Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 21 / 26
µµ Gaussian self correlation µµ ∼ R 4 receives both a Gaussian and a non-Gaussian contributions. The Gaussian is k s r − 2 6 × 10 − 17 ∆ 4 R ( k D,f ) C µµ L ∼ l, Gauss ∆ 4 k 3 R ( k p ) D,f 1 . 5 × 10 − 28 � µ fluctuations are uncorrelated at distances ∆ x ≫ 1 /k s White noise, l -independent Very small cosmic variance! Suppressed by N − 1 / 2 modes with k 3 D,f ∼ 10 12 N modes ∼ k s r − 2 L Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 22 / 26
Fisher matrix forecast NL from C µT Signal to noise for f loc l � S C µT C µT � 2 � l l = C µµ,N 1 N 2 l +1 C TT l l l A figure of merit PIXIE [Chuss et al. ’11] � √ � � 4 π × 10 − 8 S log l max 10 − 3 b f loc ≃ 80 . NL w − 1 / 2 N µ NL � 10 3 with current technology i.e. ∆ f loc It probes different scales than those of T anisotropy Enrico Pajer (Princeton) New window on primordial NG UPenn March 2012 23 / 26
Recommend
More recommend