


A new window on primordial non-Gaussianity based on 1201.5375 with M. Zaldarriaga Enrico Pajer Princeton University 2.0 � R � k � 2 � 10 9 1.5 Μ CMB � LSS 1.0 10 � 4 0.01 1 100 10 4 k Mpc
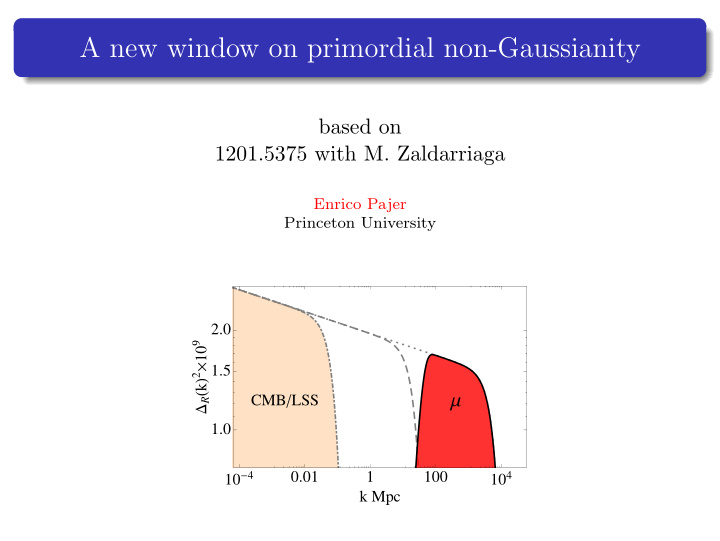
Summary We know little about primordial perturbations outside the range 10 − 4 � k Mpc � 1 µ -type spectral distortion of the CMB is a unique probe of small scales 50 � k Mpc � 10 4 [Sunyaev, Zel’dovich, Silk, Peebles, Hu, Danese, de Zotti, Chluba, . . . ] The monopole � µ (ˆ n ) � probes the small-scale power spectrum µT cross correlation probes the primordial bispectrum in the squeezed limit f loc NL Fisher forecast with current technology ∆ f loc NL � 10 3 Beat cosmic variance with an enormous number of modes Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 2 / 34
Outline 1 Motivations 2 Review of µ -distortion 3 A new window on primordial non-Gaussianity 4 Remarks Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 3 / 34
The golden age of cosmology We are living in the golden age of observational cosmology: COBE goes to Stockholm, WMAP, ACT & SPT measured the CMB with 1% accuracy. now Planck and a horde of ground and ballon based experiments Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 4 / 34
Primordial perturbations 1 H ? radiation matter dark E Log a Primordial superhorizon perturbations seed the structures in our universe They teach us about the earlier stage Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 5 / 34
The non-linear regime of structure formation Small superhorizon primordial perturbations → linear evolution Homogeneous background → no mix of different scales Perturbations re-enter the horizon → grow with time Large perturbations evolve in a complicated non-linear way → erase primordial information Linear regime: Large scale structures k < O (Mpc − 1 ) or look back in time Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 6 / 34
The cosmic microwave background A snapshot of the universe at 370 , 000 years, z ≃ 1100 Small perturbations δρ/ρ ∼ 10 − 5 → linearly related to primordial perturbations For l � 2000 or k > O (0 . 15 Mpc − 1 ) erased by diffusing damping! Can we access smaller scales? Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 7 / 34
The CMB/LSS window 2.00 1.00 0.50 outside CMB � LSS � R � k � 2 � 10 9 0.20 ? horizon Gaussian 0.10 0.05 Scale � inv 0.02 10 � 7 10 � 5 0.001 0.1 10 1000 k Mpc k � 10 − 4 Mpc − 1 are still outside our horizon k � 0 . 15 Mpc − 1 ( l � 2000) have been erased by Silk damping k � O (1) Mpc − 1 are now contaminated by gravitational non-linearities Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 8 / 34
Primordial perturbations: What do we know? Within the CMB/LSS window we know to the 1% precision [Hlozek et al. ’11] Random variable Amplitude 10 − 5 → can measure only few cumulants Almost scale invariant Adiabatic Gaussian Do these properties hold on smaller scales? Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 9 / 34
Outline 1 Motivations 2 Review of µ -distortion 3 A new window on primordial non-Gaussianity 4 Remarks Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 10 / 34
Photon thermodynamics: early times Early universe: hot photon-baryon-electron plasma Before z i ≃ 2 × 10 6 double Compton scattering ( e − + γ → e − + 2 γ ) and Bremsstrahlung are very efficient Perfect thermodynamical equilibrium. Any perturbations to the system is thermalized n � Ν � Photons can be created at low ν and re-scattered to high ν Planck spectrum 1 n ( ν ) = e ν/k B T − 1 5.0 10.0 Ν � kT 0.1 0.2 0.5 1.0 2.0 Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 11 / 34
Photon thermodynamics: µ -era Between z i and z f ∼ 5 × 10 4 double Compton scattering and bremsstrahlung are not efficient enough to create photons Elastic Compton scattering ( e − + γ → e − + γ ) maintains kinetic equilibrium Photon number is effectively frozen (except low ν ) n � Ν � A perturbation distort the spectrum Bose-Einstein spectrum with chemical potential µ 1 n ( ν ) = e ν/k B T + µ − 1 Ν � kT 0.5 1.0 2.0 5.0 Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 12 / 34
Photon thermodynamics: y-era After z f ∼ 5 × 10 4 also elastic Compton scattering is not efficient enough No kinetic equilibrium Photon number is still effectively frozen A perturbation deforms the spectrum → y-type distortion Mixing of black bodies with different T Different ν dependence. Observationally distinguishable [Khatri Chluba Sunyaev ’11] Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 13 / 34
Photon thermodynamics: decoupling After z L ≃ 10 3 photons travel without further interactions Electrons and protons combine into neutral H (and He, . . . ) Several other astrophysical foregrounds create y-distortion (mixing of black bodies) [Sunyaev Zel’dovich ’70] µ -distortion requires re-scattering of photons (kinetic equilibrium) → few contaminations! We have now a linear probe of scales 50 < k Mpc − 1 < 10 4 Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 14 / 34
Perturbations during the µ -era Perturbations during the µ -era [Khatri, Chluba Sunyaev ’11,’12] 5 × 10 4 � z � 2 × 10 6 Dissipation of acoustic modes due to diffusion damping [Silk ’72] . Scale invariant power spectrum n s ∼ 1 µ ≃ 3 × 10 − 8 Adiabatic cooling → Bose-Eistein condensation µ BE ≃ 3 × 10 − 9 Non-standard physics e.g. decays of massive particles, . . . Standard scenario: µ probes the primordial power on small scales Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 15 / 34
Dissipation of acoustic modes Perturbations of the adiabatic mode R re-enter the horizon, oscillate and dissipate δ γ ∼ R k cos( kt ) e − k 2 /k 2 D Shear viscosity and heat conduction damp the oscillations [Silk, Kaiser, Weinberg] k D ≃ z 3 / 2 4 × 10 − 6 Mpc − 1 Now we can only see � R � k � 2 � 10 9 k < k D ( z L ) ≃ 0 . 2 × Mpc − 1 z L z f 1 z i 1 µ -distortion can see 50 < k Mpc − 1 < 10 4 10 � 4 0.01 1 100 10 4 k Mpc Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 16 / 34
Power dissipated in the µ era Analytical estimate of µ [Hu et al. 94’, Khatri Chluba & Sunyaev ’11] Energy in acoustic waves ρc 2 s � δ 2 γ � δE ∼ ρ i � 3 � δ 2 γ � � � f Bose-Einstein spectrum with E → E + δE and fixed N µ ≃ 1 . 4 δE > 0 Linear integral probe of the z i � R � k � 2 � 10 9 power spectrum z L z f 1 1 Μ � d log k ∆ 2 µ ∝ R ( k ) 10 � 4 0.01 1 100 10 4 k Mpc Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 17 / 34
Relating µ to R 2 at small scales Dissipation is smeared over a volume k − 3 s Nature takes the average for us Small cosmic variance! [EP & Zaldarriaga ’12] Final analytical estimate � d 3 k 1 d 3 k 2 � k + � k 2 ) e i� R ( � k 1 ) R ( � k + · � x W µ ( x ) ≃ 6 (2 π ) 6 k s � i � e − ( k 2 1 + k 2 2 ) /k 2 ×� cos ( k 1 t ) cos ( k 2 t ) � p D f Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 18 / 34
� µ (ˆ n ) � constraints the small-scale power spectrum The averaged µ -distortion over the whole sky (monopole) [Hu et al. ’94] � � i � e − 2 k 2 /k 2 d log k ∆ 2 � µ ( x ) � ≃ 3 R ( k ) f , D Integral measure of the power spectrum at small scales For n s = 1 [Khatri Chluba Sunyaev ’12] µ ∼ 2 . 4 × 10 − 8 Needs an absolute measurement of the CMB spectrum Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 19 / 34
Outline 1 Motivations 2 Review of µ -distortion 3 A new window on primordial non-Gaussianity 4 Remarks Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 20 / 34
Primordial non-Gaussianity It is hard to tell by eye For a Gaussian random variable � δ 2 n +1 � = 0 , � δ 2 n � ∝ � δ 2 � n Non-vanishing odd correlation → non-Gaussianity δ ≪ 1 → � δ 3 � is the most sensitive Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 21 / 34
Symmetries, sizes and shapes A priori, �R 3 � depends on k 1 , k 2 , k 3 : 9 real numbers Conservation of momentum: � k 3 = − � k 1 − � k 2 2 and � Rotational invariance: only k 2 1 , k 2 k 1 · k 2 �R 3 � depends on 3 numbers �R 3 � ≡ (2 π ) 3 f NL F ( k 1 , k 2 , k 3 ) δ 3 ( k 1 + k 2 + k 3 ) Scale invariance: only k 1 /k 3 and k 2 /k 3 f NL gives the size F ( k 1 , k 2 , k 3 ) (normalized) gives the shape. Out[1320]= Enrico Pajer (Princeton) New window on primordial NG Austin Feb 2012 22 / 34
Recommend
More recommend