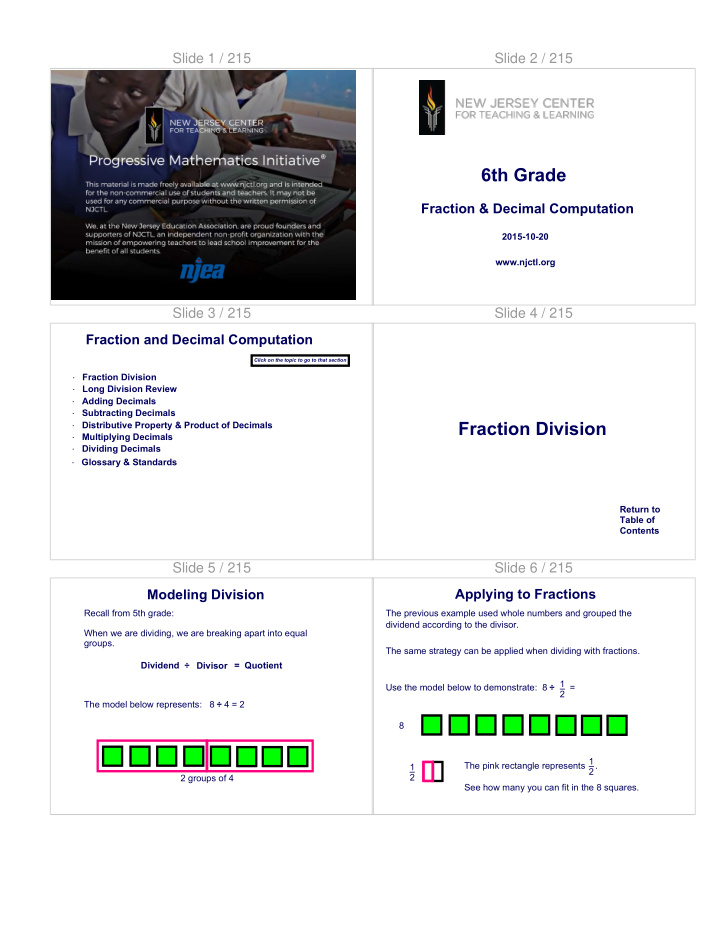



Slide 1 / 215 Slide 2 / 215 6th Grade Fraction & Decimal Computation 2015-10-20 www.njctl.org Slide 3 / 215 Slide 4 / 215 Fraction and Decimal Computation Click on the topic to go to that section Fraction Division · Long Division Review · Adding Decimals · Subtracting Decimals · Fraction Division Distributive Property & Product of Decimals · Multiplying Decimals · Dividing Decimals · Glossary & Standards · Return to Table of Contents Slide 5 / 215 Slide 6 / 215 Modeling Division Applying to Fractions Recall from 5th grade: The previous example used whole numbers and grouped the dividend according to the divisor. When we are dividing, we are breaking apart into equal groups. The same strategy can be applied when dividing with fractions. Dividend ÷ Divisor = Quotient 1 Use the model below to demonstrate: 8 ÷ = 2 The model below represents: 8 ÷ 4 = 2 8 1 The pink rectangle represents . 1 2 2 2 groups of 4 See how many you can fit in the 8 squares.
Slide 7 / 215 Slide 8 / 215 Example 1 Evaluate the following problem using the model below. 1 Use the model below to demonstrate 2 ÷ = 3 1 3 ÷ = 4 2 3 1 3 1 4 Slide 9 / 215 Slide 10 / 215 Visual Model 2 Evaluate the following problem using the model below. A fraction can be divided by a whole number using the following visual model. 1 5 ÷ = 3/5 ÷ 4 2 3 4 1 2 Divide into 4 groups 5 1 2 Slide 11 / 215 Slide 12 / 215 Word Problem The previous expression can be represented by the following word problem: How much will each person receive if 4 friends share a 3/5 pound bag of popcorn? 1 2 3 4 Each friend will receive 3/20 lb. of popcorn.
Slide 13 / 215 Slide 14 / 215 Slide 15 / 215 Slide 16 / 215 Slide 17 / 215 Slide 18 / 215
Slide 19 / 215 Slide 20 / 215 Patterns Vocabulary Review Do you notice a pattern between the division of fractions and Complex Fraction : A fraction with another fraction in the their solution? numerator, denominator or both. Reciprocal : The inverse of a number/fraction. Original 4 Number Reciprocal 2 Slide 21 / 215 Slide 22 / 215 Example If you think about it, we are dividing by a fraction which creates a complex fraction. 1 1 x 3 1 x 3 2 2 2 2 2 1 2 1 x 3 = = = You need to eliminate the fraction in the denominator in order = 2 2 3 2 x 3 2 1 2 to solve the problem. 3 3 2 To do this, multiply the numerator and denominator of the Original Simplify Rewrite Complex Multiply by complex fraction by the reciprocal of the denominator (making Problem Fraction Denominator Without 1 Reciprocal the denominator = 1). There are rules that can be applied to fraction You can then simplify the fraction by rewriting it without the division problems to eliminate steps from this denominator of 1 and solve the new multiplication problem. lengthy procedure. source - http://www.helpwithfractions.com/dividing-fractions.html Slide 23 / 215 Slide 24 / 215 Dividing Fractions Algorithm Dividing Fractions Algorithm Some people use the saying " Keep Change Flip" Algorithm to help them remember the algorithm. Step 1: Leave the first fraction the same. Change Changed Step 2: Multiply the first fraction by the reciprocal of the Keep Flip Flipped Kept second fraction. 3 7 3 8 3 x 8 = 24 = = x 5 8 5 7 5 x 7 35 Step 3: Simplify your answer. 1 1 1 x 2 = 1 x 2 = 2 = 5 2 5 1 5 x 1 5
Slide 25 / 215 Slide 26 / 215 Checking Your Answer To check your answer, use your knowledge of fact families. 3 7 24 ÷ = 5 8 35 3 7 24 = x 5 8 35 3 7 24 of is 5 8 35 Slide 27 / 215 Slide 28 / 215 7 ) 8 ) 2 7 4 8 = 5 x 8 3 2 = 8 5 10 4 10 4 7 True True False False Slide 29 / 215 Slide 30 / 215 10 ) 9 ) 4 8 = 5 10 A 1 39 B 40 40 C 42
Slide 31 / 215 Slide 32 / 215 Simplify 11 ) Sometimes you can cross simplify prior to multiplying. without cross with cross simplifying simplifying 1 5 2 3 Slide 33 / 215 Slide 34 / 215 12 Can this problem be cross simplified? 13 Can this problem be cross simplified? Yes Yes No No Slide 35 / 215 Slide 36 / 215 14 Can this problem be cross simplified? 15 Can this problem be cross simplified? Yes Yes No No
Slide 37 / 215 Slide 38 / 215 16 ) 17 ) Slide 39 / 215 Slide 40 / 215 18 ) 19 ) Slide 41 / 215 Slide 42 / 215 Visual Model Visual Model A mixed number can be divided by a mixed number using the Since our LCD is 6, every 6 lines is considered a whole. following visual model. 1 1/2 is equivalent to 9 sections on the number line. 1 1/2 First find the least common denominator (LCD) which is 6. 9 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 7 8 If every 6 lines represents a whole, then how many lines 2 2/3 should we draw to make sure both mixed numbers fit? 2 2/3 is equivalent to 16 sections on the number line. So 1 1/2 ÷ 2 2/3 = 9/16
Slide 43 / 215 Slide 44 / 215 Visual Model Dividing Mixed Numbers Algorithm What if the problem were written as ? Step 1: Rewrite the Mixed Number(s) as an improper fraction(s). (write whole numbers / 1) 2 2/3 Step 2: Follow the same steps for dividing fractions 5 9 10 11 12 13 14 15 16 17 18 1 2 3 4 6 7 8 1 1/2 1 1/2 1 6 3 6 x 2 = 12 = 4 1 = 6 = 2 1 2 1 3 3 How many times does 1 1/2 divide into 2 2/3? Slide 45 / 215 Slide 46 / 215 Example 20 ) 1 2 2 Evaluate: 1 = 2 3 2 1 5 7 5 x 2 = 10 1 3 = = 3 2 2 3 3 7 21 Slide 47 / 215 Slide 48 / 215 21 ) 22 ) 1 2 5 1 2 5 4 = = 2 5 2
Slide 49 / 215 Slide 50 / 215 Application Problem 23 ) 1 2 3 3 Winnie needs pieces of string for a craft project. How many 1/6 yd = pieces of string can she cut from a piece that is 2/3 yd long? 2 8 2 1 ÷ 3 6 6 12 2 4 4 pieces x = = 3 1 3 1 or 2 6 2 4 1 = 4 pieces x = 3 1 1 Slide 51 / 215 Slide 52 / 215 Application Problem Application Problem Kristen is making a ladder and wants to cut ladder rungs from a 6 ft One student brings 1/2 yd of ribbon. If 3 students receive an board. Each rung needs to be 3/4 ft long. How many ladder rungs equal length of the ribbon, how much ribbons will each student can she cut? receive? 3 1 6 ÷ 4 ÷ 3 2 6 3 1 x 1 1 1 ÷ yards of ribbon 4 = 2 3 6 6 4 24 8 1 x = = = 8 rungs 3 3 1 Slide 53 / 215 Slide 54 / 215 Application Problem 24 Robert bought 3/4 pound of grapes and divided them into 6 equal portions. What A box weighing 9 1/3 lb contains toy robots weighing 1 1/6 lb is the weight of each portion? apiece. How many toy robots are in the box? A 8 pounds 9 1 1 1 ÷ B 4 1/2 pounds 3 6 C 2/5 pounds D 1/8 pound 7 28 ÷ 6 3 4 2 28 6 8 x = = 8 robots 3 7 1 1 1
Slide 55 / 215 Slide 56 / 215 25 A car travels 83 7/10 miles on 2 1/4 26 One tablespoon is equal to 1/16 cup. It is gallons of fuel. Which is the best estimate also equal to 1/2 ounce. A recipe uses 3/4 of the number miles the car travels on cup of flour. How many tablespoons of one gallon of fuel? flour does the recipe use? A 84 miles A 48 tablespoons B 62 miles B 24 tablespoons C 42 miles C 12 tablespoons D 38 miles D 6 tablespoons Slide 57 / 215 Slide 58 / 215 27 A bookstore packs 6 books in a box. The 28 There is gallon of distilled water in the total weight of the books is 14 2/5 pounds. If each book has the same class science supplies. If each pair of weight, what is the weight of one book? students doing an experiment uses A 5/12 pound B 2 2/5 pounds gallon of distilled water, there will be C 8 2/5 pounds D 86 2/5 pounds gallon left in the supplies . How many students are doing the experiments? Slide 59 / 215 Slide 60 / 215 29 Carol makes cups of snack mix. She 30 Part A A group of hikers buy 8 bags of trail mix. puts all the snack mix into plastic bags. She Each bag contains cups of trail mix. The puts cup of the snack mix in each bag. trail mix is shared evenly among 12 hikers. How many plastic bags does Carol need? How many cups of trail mix will each hiker Enter your answer in the box. receive? Show your work or explain your bags answer. From PARCC EOY sample test non-calculator #9 From PARCC PBA sample test calculator #10
Recommend
More recommend