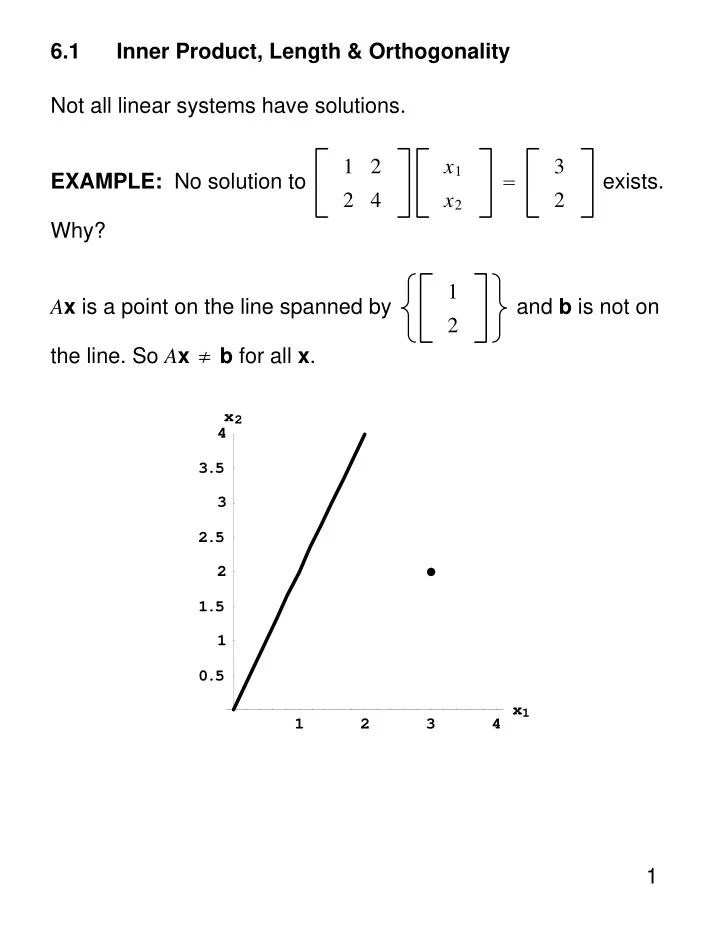
6.1 Inner Product, Length & Orthogonality Not all linear - PDF document

6.1 Inner Product, Length & Orthogonality Not all linear systems have solutions. 1 2 3 x 1 EXAMPLE: No solution to exists. = 2 4 2 x 2 Why? 1 A x is a point on the line spanned by and b is not on 2 the line. So A x ≠ b for all x . x 2 4 3.5 3 2.5 2 1.5 1 0.5 x 1 1 2 3 4 1

Instead find  x so that A  x lies ”closest” to b . x 2 4 3.5 3 2.5 2 1.5 1 0.5 x 1 1 2 3 4 Using information we will learn in this chapter, we will find that 1.4 1. 4  , so that A  x = x = . 0 2. 8 Segment joining A  x and b is perpendicular ( or orthogonal) to the set of solutions to A x = b . Need to develop fundamental ideas of length , orthogonality and orthogonal projections . 2

The Inner Product Inner product or dot product of u 1 v 1 u 2 v 2 u = and v = : ⋮ ⋮ u n v n v 1 v 2 u ⋅ v = u T v = u 1 u 2 ⋯ u n = ⋮ v n u 1 v 1 + u 2 v 2 + ⋯ + u n v n Note that v ⋅ u = v 1 u 1 + v 2 u 2 + ⋯ + v n u n = u 1 v 1 + u 2 v 2 + ⋯ + u n v n = u ⋅ v 3

THEOREM 1 Let u , v and w be vectors in R n , and let c be any scalar. Then a. u ⋅ v = v ⋅ u b.  u + v  ⋅ w = u ⋅ w + v ⋅ w c.  c u  ⋅ v = c  u ⋅ v  = u ⋅  c v  d. u ⋅ u ≥ 0 , and u ⋅ u = 0 if and only if u = 0 . Combining parts b and c, one can show  c 1 u 1 + ⋯ + c p u p  ⋅ w = c 1  u 1 ⋅ w  + ⋯ + c p  u p ⋅ w  4

Length of a Vector v 1 v 2 For v = , the length or norm of v is the nonnegative ⋮ v n scalar ‖ v ‖ defined by 2 + v 2 2 + ⋯ + v n ‖ v ‖ 2 = v ⋅ v . 2 ‖ v ‖ = v ⋅ v = and v 1 a a 2 + b 2 For example, if v = , then ‖ v ‖ = (distance b between 0 and v ) Picture: For any scalar c , ‖ c v ‖ = | c | ‖ v ‖ 5

Distance in R n The distance between u and v in R n : dist  u , v  = ‖ u − v ‖ . This agrees with the usual formulas for R 2 and R 3 . Let u =  u 1 , u 2  and v =  v 1 , v 2  . Then u − v =  u 1 − v 1 , u 2 − v 2  and dist  u , v  = ‖ u − v ‖ = ‖  u 1 − v 1 , u 2 − v 2  ‖  u 1 − v 1  2 +  u 2 − v 2  2 = 6

Orthogonal Vectors  dist  u , v  2 = ‖ u − v ‖ 2 =  u − v  ⋅  u − v  =  u  ⋅  u − v  +  − v  ⋅  u − v  = = u ⋅ u − u ⋅ v + − v ⋅ u + v ⋅ v =‖ u ‖ 2 + ‖ v ‖ 2 − 2 u ⋅ v  dist  u , v  2 = ‖ u ‖ 2 + ‖ v ‖ 2 − 2 u ⋅ v ⇒ Similarly,  dist  u , − v  2 = ‖ u ‖ 2 + ‖ v ‖ 2 + 2 u ⋅ v 7

Since  dist  u , − v  2 =  dist  u , v  2 , u ⋅ v = ___. Two vectors u and v are said to be orthogonal (to each other) if u ⋅ v = 0 . Also note that if u and v are orthogonal, then ‖ u + v ‖ = ‖ u ‖ 2 + ‖ v ‖ 2 . THEOREM 2 THE PYTHAGOREAN THEOREM Two vectors u and v are orthogonal if and only if ‖ u + v ‖ = ‖ u ‖ 2 + ‖ v ‖ 2 . 8

Orthogonal Complements If a vector z is orthogonal to every vector in a subspace W of R n , then z is said to be orthogonal to W . The set of vectors z that are orthogonal to W is called the orthogonal complement of W and is denoted by W ⊥ (read as “W perp”). 9

Row, Null and Columns Spaces THEOREM 3 Let A be an m × n matrix. Then the orthogonal complement of the row space of A is the nullspace of A , and the orthogonal complement of the column space of A is the nullspace of A T : ⊥ = Nul A , ⊥ = Nul A T . Row A Col A Why? (See complete proof in the text) Consider A x = 0 : 0 ⋯ ⋆ ∗ ∗ ∗ 0 ⋯ ⋆ ∗ ∗ ∗ = ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ 0 ⋯ ⋆ ∗ ∗ ∗ r 1 ⋅ x 0 0 r 2 ⋅ x Note that A x = and so x is orthogonal to = ⋮ ⋮ r m ⋅ x 0 the row A since x is orthogonal to r 1 . … , r m . 10

1 0 − 1 EXAMPLE: Let A = . 2 0 2 0 1 Basis for Nul A = , and therefore Nul A is a 1 0 0 1 plane in R 3 . 1 Basis for Row A = and therefore Row A is a line 0 − 1 in R 3 . 1 and therefore Col A is a line in R 2 . Basis for Col A = 2 − 2 and therefore Nul A T is a line in Basis for Nul A T = 1 R 2 . 11

Subspaces Nul A and Row A x 2 4 2 x 1 − 4 − 2 2 4 − 2 − 4 Subspaces Nul A T and Col A 12