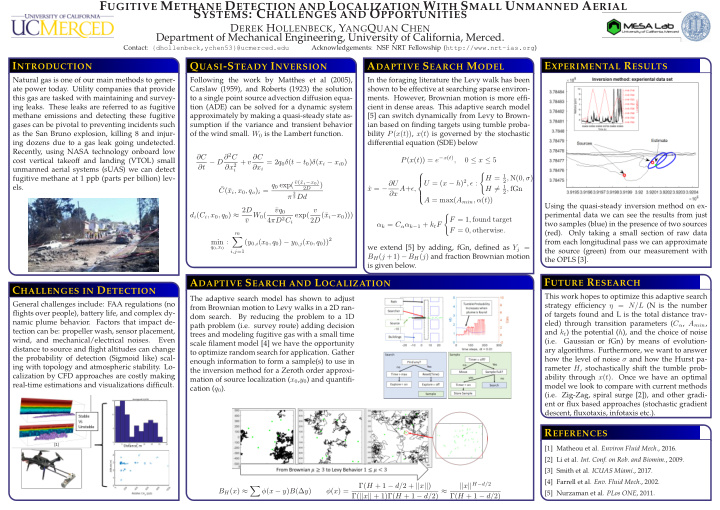



F UGITIVE M ETHANE D ETECTION AND L OCALIZATION W ITH S MALL U NMANNED A ERIAL S YSTEMS : C HALLENGES AND O PPORTUNITIES D EREK H OLLENBECK , Y ANG Q UAN C HEN Department of Mechanical Engineering, University of California, Merced. Contact: {dhollenbeck,ychen53}@ucmerced.edu Acknowledgements: NSF NRT Fellowship ( http://www.nrt-ias.org ) I NTRODUCTION E XPERIMENTAL R ESULTS Q UASI -S TEADY I NVERSION A DAPTIVE S EARCH M ODEL Natural gas is one of our main methods to gener- Following the work by Matthes et al (2005), In the foraging literature the Levy walk has been ate power today. Utility companies that provide Carslaw (1959), and Roberts (1923) the solution shown to be effective at searching sparse environ- this gas are tasked with maintaining and survey- to a single point source advection diffusion equa- ments. However, Brownian motion is more effi- ing leaks. These leaks are referred to as fugitive tion (ADE) can be solved for a dynamic system cient in dense areas. This adaptive search model methane emissions and detecting these fugitive approximately by making a quasi-steady state as- [5] can switch dynamically from Levy to Brown- gases can be pivotal to preventing incidents such sumption if the variance and transient behavior ian based on finding targets using tumble proba- of the wind small. W 0 is the Lambert function. bility P ( x ( t )) , x ( t ) is governed by the stochastic as the San Bruno explosion, killing 8 and injur- ing dozens due to a gas leak going undetected. differential equation (SDE) below Recently, using NASA technology onboard low ∂t − D∂ 2 C ∂C + v ∂C P ( x ( t )) = e − x ( t ) , 0 ≤ x ≤ 5 cost vertical takeoff and landing (VTOL) small = 2 q 0 δ ( t − t 0 ) δ ( x i − x i 0 ) ∂x 2 ∂x i unmanned aerial systems (sUAS) we can detect i � H = 1 2 , N(0 , σ ) fugitive methane at 1 ppb (parts per billion) lev- U = ( x − h ) 2 , ǫ : x i , x 0 , q o ) i = q 0 exp( ¯ v (¯ x i − x 0 ) x = − ∂U ) els. H � = 1 ¯ ˙ ∂x A + ǫ, 2 , fGn 2 D C (¯ 2 3 Dd π A = max( A min , α ( t )) Using the quasi-steady inversion method on ex- d i ( C i , x 0 , q 0 ) ≈ 2 D vq 0 ¯ exp( v v W 0 ( 2 D (¯ x i − x 0 ))) perimental data we can see the results from just � F = 1 , found target 4 πD 2 C i ¯ two samples (blue) in the presence of two sources α k = C α α k − 1 + k t F F = 0 , otherwise . (red). Only taking a small section of raw data m � ( y 0 ,i ( x 0 , q 0 ) − y 0 ,j ( x 0 , q 0 )) 2 q 0 ,x 0 : min from each longitudinal pass we can approximate we extend [5] by adding, fGn, defined as Y j = the source (green) from our measurement with i,j =1 B H ( j + 1) − B H ( j ) and fraction Brownian motion the OPLS [3]. is given below. F UTURE R ESEARCH A DAPTIVE S EARCH AND L OCALIZATION C HALLENGES IN D ETECTION This work hopes to optimize this adaptive search The adaptive search model has shown to adjust General challenges include: FAA regulations (no strategy efficiency η = N/L (N is the number from Brownian motion to Levy walks in a 2D ran- flights over people), battery life, and complex dy- of targets found and L is the total distance trav- dom search. By reducing the problem to a 1D namic plume behavior. Factors that impact de- eled) through transition parameters ( C α , A min , path problem (i.e. survey route) adding decision tection can be: propeller wash, sensor placement, and k t ) the potential ( h ), and the choice of noise trees and modeling fugitive gas with a small time wind, and mechanical/electrical noises. Even (i.e. Gaussian or fGn) by means of evolution- scale filament model [4] we have the opportunity distance to source and flight altitudes can change ary algorithms. Furthermore, we want to answer to optimize random search for application. Gather the probability of detection (Sigmoid like) scal- how the level of noise σ and how the Hurst pa- enough information to form a sample(s) to use in ing with topology and atmospheric stability. Lo- rameter H , stochastically shift the tumble prob- the inversion method for a Zeroth order approxi- calization by CFD approaches are costly making ability through x ( t ) . Once we have an optimal mation of source localization ( x 0 , y 0 ) and quantifi- real-time estimations and visualizations difficult. model we look to compare with current methods cation ( q 0 ). (i.e. Zig-Zag, spiral surge [2]), and other gradi- ent or flux based approaches (stochastic gradient descent, fluxotaxis, infotaxis etc.). R EFERENCES [1] Matheou et al. Environ Fluid Mech. , 2016. [2] Li et al. Int. Conf. on Rob. and Biomim. , 2009. [3] Smith et al. ICUAS Miami. , 2017. [4] Farrell et al. Env. Fluid Mech. , 2002. || x || H − d/ 2 Γ( H + 1 − d/ 2 + || x || ) � B H ( x ) ≈ φ ( x − y ) B (∆ y ) φ ( x ) = Γ( || x || + 1)Γ( H + 1 − d/ 2) ≈ [5] Nurzaman et al. PLos ONE , 2011. Γ( H + 1 − d/ 2)
Very Slow Diffusion Processes and its Regional Analysis ICERM FPDE Workshop 2018, Brown University Presenter: Dr. YangQuan Chen The MESA Lab, University of California, Merced Joint work with Ruiyang Cai (Donghua University, China) and Yuquan Chen (University of Science and Technology of China) June 21, 2018 June 21, 2018 () June 21, 2018 1 / 43
Main Contents 1. Very Slow Tail Background Comparison with other tails Laplace transform of the very slow kernel 2. New Fractional Integral and Derivative Definitions Integral and derivative of some special functions Realization of L − 1 � � log s ( t ) by NILT and Prony s α ( s − 1) 3. Regional Analysis Introduction to the regional analysis Regional observability and controllability 4. Further Research Directions 5. Main References () June 21, 2018 2 / 43
Very Slow Tail Background Background Figure: Tesla Model S/X Mileage VS Remaining Battery Capacity () June 21, 2018 3 / 43
Very Slow Tail Background Background Figure: Tesla Model S/X Battery Age VS Remaining Battery Capacity () June 21, 2018 4 / 43
Very Slow Tail Background Some Links https://docs.google.com/spreadsheets/d/t024 bMoRiDPIDialGnuKPsg/edit#gid=1669966328 https://docs.google.com/spreadsheets/d/t024 bMoRiDPIDialGnuKPsg/edit#gid=154312675 For more details, see [1]. () June 21, 2018 5 / 43
Very Slow Tail Background Background Figure: Human feet as a geological force https://twitter.com/PaulMMCooper/status/1007612133356572672 () June 21, 2018 6 / 43
Very Slow Tail Comparison with other tails Different tails to describe decay rate For the above data, t − α is too fast while (log t ) − α is too slow Very Slow between power-law and ultra-slow? Yes! A new tail for very-slow: log t t α () June 21, 2018 7 / 43
Very Slow Tail Comparison with other tails Image of these kernels: x label-t α =0.25 α =0.5 1.5 0.8 0.6 1 0.4 0.5 0.2 0 0 0 500 1000 0 500 1000 α =0.75 α =1 0.6 0.6 exp(-t)/t α log(t)/t α 0.4 0.4 1/t α 1/(log(t)) α 0.2 0.2 0 0 0 500 1000 0 500 1000 () June 21, 2018 8 / 43
Very Slow Tail Comparison with other tails Image of these kernels: x label-log t α =0.25 α =0.5 1.5 0.8 0.6 1 0.4 0.5 0.2 0 0 2 4 6 8 2 4 6 8 α =0.75 α =1 0.6 0.6 exp(-t)/t α log(t)/t α 0.4 0.4 1/t α 1/(log(t)) α 0.2 0.2 0 0 2 4 6 8 2 4 6 8 () June 21, 2018 9 / 43
Very Slow Tail Comparison with other tails Comparison between log t 1 t α and (log t ) α when α = 0 . 25 x-lable: t 1.5 log(t)/t α 1/(log(t)) α 1 0.5 0 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 × 10 6 x-lable: log t 1.5 log(t)/t α 1/(log(t)) α 1 0.5 0 10 1 10 2 10 3 10 4 10 5 10 6 10 7 () June 21, 2018 10 / 43
Very Slow Tail Laplace transform of the very slow kernel The Laplace transform of the very slow kernel is � log t � ( s ) = s α − 1 Γ(1 − α ) ( ψ (1 − α ) − log s ) , L t α where ψ ( x ) = Γ ′ ( x ) Γ( x ) denotes the digamma function. () June 21, 2018 11 / 43
Very Slow Tail Realization of the kernel in engineering by Prony 10 actual impulse response approximate impulse response 0 -10 -20 -30 -40 -50 0 1 2 3 4 5 6 7 8 9 10 Figure: Prony: α =0.5, order=12, t=10, Ts=0.01 () June 21, 2018 12 / 43
Very Slow Tail Realization of the kernel in engineering by Prony 40 20 margin 0 -20 10 -2 10 -1 10 0 10 1 10 2 frequency 200 100 phase 0 -100 -200 10 -2 10 -1 10 0 10 1 10 2 frequency Figure: Bode diagram: α =0.5, order=12 () June 21, 2018 13 / 43
Very Slow Tail Realization of the kernel in engineering by Prony Pole-Zero Map 1 0.8 0.6 0.4 Imaginary Axis 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -1 -0.5 0 0.5 1 1.5 Real Axis Figure: Pole-Zero: α =0.5, order=12 () June 21, 2018 14 / 43
New Fractional Integral and Derivative Definitions α -th order fractional integral: � t 1 log( t − s ) 0 I α t f ( t ) � ( t − s ) 1 − α f ( s ) ds Γ( α ) 0 α -th order Riemann-Liouville type fractional derivative: � t 1 d log( t − s ) 0 D α t f ( t ) � ( t − s ) α f ( s ) ds Γ(1 − α ) dt 0 α -th order Caputo type fractional derivative: � t 1 log( t − s ) C 0 D α t f ( t ) � ( t − s ) α f ′ ( s ) ds Γ(1 − α ) 0 () June 21, 2018 15 / 43
New Fractional Integral and Derivative Properties D α f ( t ) = d dt I 1 − α f ( t ) t f ( t ) � = 0 I α + β 0 I β t 0 I β t 0 I α t f ( t ) = 0 I α f ( t ) t 0 D β t 0 D β t f ( t ) � = 0 D α + β t 0 D α t f ( t ) = 0 D α f ( t ) t 0 D β 0 D β 0 D α + β C C 0 D α t f ( t ) = C 0 D α C t f ( t ) � = C f ( t ) t t t () June 21, 2018 16 / 43
Recommend
More recommend