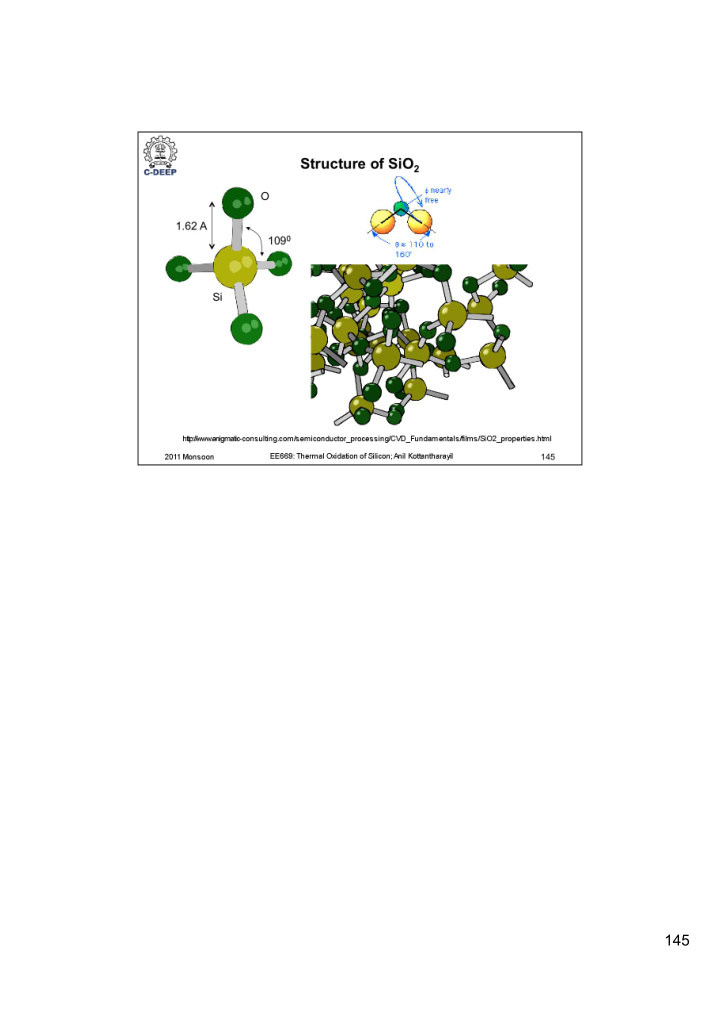



145
Both the diffusion processes and the chemical reaction are thermally activated processes. E 1 and E 2 are the activation energies of the rate constants. The activation energy of the linear growth constants are almost identical for both the cases. This implies that the rate limiting reaction is the same for both. From independent experiments, it has been ascertained that the activation energy for Si- Si bond breaking is ~ 2 eV. So the rate limiting reaction at the interface is the Si-Si bond breaking. The pre-factor C 2 is higher for H 2 O which is related to the fact that the solubility of H 2 O in SiO 2 is larger. The activation energy for the parabolic rate constant is smaller for H 2 O than for O 2 . Again the activation energies correlate well with the activation energies of H 2 O and O 2 diffusion in SiO 2 . The earlier mentioned possibility that the H 2 O absorbed in the SiO 2 weakens the material enhancing diffusion could be the reason. 146
The plots show the oxide growth for wet and dry oxidation based on the Deal-Grove model. So this is theory. In general the growth is faster in wet oxidation process. There are two reasons: the solubility of H 2 O in SiO 2 is 3 orders of magnitude higher than the solubility of O 2 . So both B and B/A would be higher for H 2 O. The activation energy for diffusion of H 2 O is smaller than for O 2 . 147
It is observed that the experimental data deviates from the Deal-Grove model for thickness below ~ 30 nm for dry oxidation. The graphs show the data from the original paper by Deal and Grove. It is seen that the theory predicts the oxidation for thickness > 30nm. However the oxidation rate is seen to be significantly higher for thinner oxides. It should be noted that several applications require oxides of thickness < 30nm. 148
One of the key difficulty in understanding the thin oxide growth regime is the fact that the cleaning procedure has a significant impact on the growth of thin oxides. The figure shows oxide growth data on wafers cleaned by various procedures. It is seen that in the ~ 25 nm thickness nominal thickness of the oxide, the variation depending on the cleaning procedure is ~ 7 nm, a 30% variation. The other aspects to be considered are that the surface of the wafer can be passivated with an extremely thin layer of native SiO2 in wafers cleaned with a finishing step of DI water rinse and for HF last clean, the wafer surface would be covered with Si-H bonds. The native oxide in turn would have absorbed water which can act as the oxidant species during the initial stages of oxidation. This could lead to high growth rate during the initial stage. However in pyrogenic or wet oxidation, the intentionally used oxidant is water. There is hardly any difference in the oxidant in the initial stages and and later part of the oxidation. 149
Several models have been proposed in the literature. We would just glance over two of them. If you are interested to more, you can check the book by Plummer and the references therein. ε is the permittivity of the oxide and C is the concentration of the oxidant ions in the oxide. Assuming that all the oxidant dissolved in the oxide at the process temperature are ionized, C is nothing but the solubility of the oxidant species in the oxide. For O 2 this is ~ 5 x 10 16 cm -3 at 1100C and for H 2 O this is ~ 3 x 10 19 cm -3 . The value of the Debye length calculated in the two cases are 15 nm (dry oxidation) and 1 nm (wet oxidation). However this model is not widely accepted today as the oxidant species, especially in the case of O 2 , is believed to diffuse in molecular form. The model used by many workers is a slightly modified version of the Deal – Grove model. The model is empirical in the sense that it can be fitted well to experimental data, but the physical origin is doubtful. The first term in the growth rate equation is the Deal-Grove model. The second term is added by Massoud and co workers. The value of L is ~ 7nm (7 x 10 -7 cm) . For x O significantly higher than this, the second term in the differential equation would be negligible. E A = 2.35 eV and C O ~ 0.001 cm/sec. 150
H is the Henry constant and P is the pressure. If we use a gas mixture, the C O for the oxidant would be proportional to the partial pressure of the oxidant in the mixture. This implies that both the parabolic and linear rate constants are proportional to pressure. However this is seen to be valid only for wet oxidation. In the case of dry oxidation, B is seen to be proportional to the pressure, whereas the linear rate constant is not proportional to pressure. It is likely that the reaction rate is dependent on the pressure. 151
Oxidation rate is seen to be dependent on the crystal orientation, especially for thin oxides. A consequence of this in a 3D structure can be appreciated by analyzing the case of FinFET. FinFET is a fully depleted enhancement mode MOSFET, wherein the gate is wrapped on 3 sides of a fin like structure. These are typically made on SOI. However they can also be made on bulk silicon wafers. Suppose that the SOI wafer orientation is (001) and the fin is etched so that the sidewalls of the fin is on the (110) plane. If the oxide growth has different rates on the top (001) and sidewall (110), we have a problem in that the gate leakage at the top would be higher whereas the gate control on the side walls would be less. Even though this is a good example, it should be understood that FinFET devices are being used for extremely scaled devices with high-k gate dielectric which are deposited by atomic layer deposition (ALD). ALD guarantees conformal deposition (same thickness on top and on the side walls). However early FinFETs were made with thermally grown SiO 2 . 152
153
154
155
156
157
Recommend
More recommend