UMBC A B M A L T F O U M B C I M Y O R T 1 - PowerPoint PPT Presentation

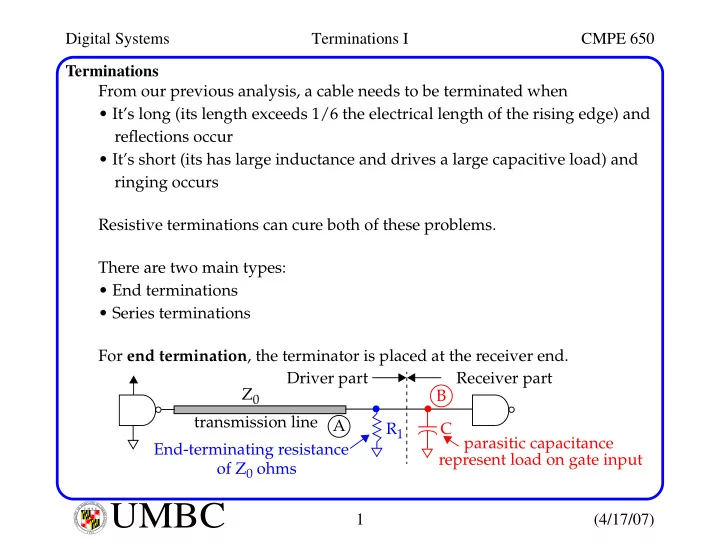
Digital Systems Terminations I CMPE 650 Terminations From our previous analysis, a cable needs to be terminated when • It’s long (its length exceeds 1/6 the electrical length of the rising edge) and reflections occur • It’s short (its has large inductance and drives a large capacitive load) and ringing occurs Resistive terminations can cure both of these problems. There are two main types: • End terminations • Series terminations For end termination , the terminator is placed at the receiver end. Driver part Receiver part Z 0 B transmission line A R 1 C parasitic capacitance End-terminating resistance represent load on gate input of Z 0 ohms L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 1 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 End Terminations Characteristics: • The driving wfm propagates at full intensity all the way down the cable • All reflections are damped by the terminating resistor • The received voltage is equal to the transmitted voltage Rise time : The Thevenin equivalent driving impedance is the transmission line impedance Z 0 , in parallel with the terminating resistor (also Z 0 ). This yields a drive impedance (for short term events) of Z 0 /2. The receiving part consists of a load capacitor (a good model for CMOS, TTL or ECL). Therefore, this RC filter has a time constant: Z 0 Z 0 previously τ - C T 10-90 - C 1.1 Z 0 C = - - - - - = 2.2 - - - - - = we formulated 2 2 L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 2 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 End Terminations The point B rise time is then computed from the "averaging method": 2 2 T B T 10-90 T 1 T 1 is the incoming signal rise time = + This is a good model if the line is long. When it is short (i.e., comparable to the length of its rising edge), the imped- ance as seen at B goes down. In the limit, the driving impedance is just the output impedance of the driver. This gives a faster rise time at point B . See the text for a derivation using our previous model for a transmission line: A ω ( ) H x ω ( ) R 2 ω ( ( ) ) + 1 S ∞ ω ( ) = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ω R 2 ω ( ) H x ( ) R 1 ω ( ) 1 – An end-terminated capacitively coupled rise time is half that of a series termi- nated line (described below) under the same load conditions. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 3 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 End Terminations The termination arrangement just discussed rarely appears in TTL or CMOS circuits because of the large drive current to maintain a high state. The driver must supply V CC /R 1 to the terminating resistor. With Z 0 equal to 65- Ω , a 5-V signal requires 5/65 = 76mA! Alternatively, one can use a split termination : Driver part Receiver part R 1 Z 0 B transmission line A R 2 C parasitic capacitance R 1 ||R 2 is Z 0 ohms represent load on gate input Here, the ratio R 1 / R 2 controls the relative proportion of high vs low current. This type of termination is sometimes used to terminate ECL circuits. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 4 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 End Terminations Setting R 1 = R 2 equalizes the current requirements for use with HCMOS. If R 2 > R 1 , low current exceeds high current, appropriate for TTL and HCT. The selection of R 1 and R 2 can be done graphically under 3 constraints: • The parallel combination must equal Z 0 . • We must not exceed I OHmax (max high-level output current) or I OLmax . Assume sink current (entering the driver) is positive and source current is negative. TTL and CMOS sinks current in low state and sources current in high state while ECL sources current in both states. In order to keep our constraint equations linear, we use admittances : 1 1 1 Y 1 Y 2 Y 1 Y 2 & + = - - - - - - = - - - - - - = - - - - - - Z 0 R 1 R 2 L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 5 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 End Terminations This constraint can be graphed: Y 1 5.5V I OH constraint: R 1 0.7 Y 1 - 4.8 Y 2 > -0.024 5V 0.02 I driver I OL constraint: 5.06 Y 1 - 0.44 Y 2 < 0.024 0.01 R 2 Sum of constants 74HC11000 NAND Y 2 Region satisfying 0.01 0.02 is 5.5V. gate analysis both constraints 100 Ω Difference 65 Ω gives current constraint line through driver All valid combinations of Y 1 and Y 2 lie on the green and blue lines for a given Z 0 . The equations for the two other constraints is derived by noting the current that flows in the driver equals the current flowing in R 2 minus R 1 . L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 6 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 End Terminations These currents depend on V CC , V EE and the driver output voltage. ( ) Y 1 ( ) Y 2 > V CC V OH V OH V EE I OHmax – – – high output state ( ) Y 1 ( ) Y 2 < V CC V OL V OL V EE I OLmax – – – low output state Note the left and right members of I OHmax equation are negative numbers. Also, the value of I OLmax is a positive number for TTL and CMOS but is zero for ECL. The 100- Ω line shown in the graph passes the constraint line limits and yields resistance values for R 1 and R 2 of 200 Ω . On the other hand, the 65- Ω line does not satisfy both current constraints at any point, and therefore cannot drive a 65- Ω load. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 7 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 Other Topologies Used with End Terminations The bifurcated line cannot be terminated properly since signal energy will always refl ects of f the junction at point A , causing ringing. Z 0 5V A Z 0 Z 0 However, the following configuration can be properly terminated: 2Z 0 5V R 1 = 2 Z 0 A Z 0 These lines are 2Z 0 skinner than main feed R 2 = 2 Z 0 Not often used because of the difficulty to fabricate L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 8 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 Other Topologies Used with End Terminations End termination allows receivers to be placed at any point along the line. Each receiver sees a delayed version of the signal. 5V Daisy chain configuration Main path Each adds a capacitive load that degrades rise time Keep the connecting stubs short compared to the length of the rising edge to avoid refl ections at the bifur cation points. Right way Wrong way From From Driver Driver L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 9 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Terminations I CMPE 650 Power Dissipation in End Terminators Load dissipation is inversely proportional to the terminating impedance and obviously depends on the high and low operating voltages. Under the assumption that equal amounts of time are spent in the high and low states, the power dissipated in the load resistors is given by: ) 2 ) 2 ) 2 ) 2 ( ( ( ( V HI V EE V LO V EE V CC V HI V CC V LO – + – – + – P load = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - + - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 R 2 2 R 1 The power dissipated in the driving circuit was discussed previously. Source Terminators This scheme connects the driver to the impedance line through a resistor. The sum of the driver source impedance plus this resistor should equal Z 0 (the characteristic impedance of the transmission line). Under these conditions, the refl ection coef ficient at the src is zero. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 10 (4/17/07) I E S R C E O V U I N N U T Y 1 6 9 6