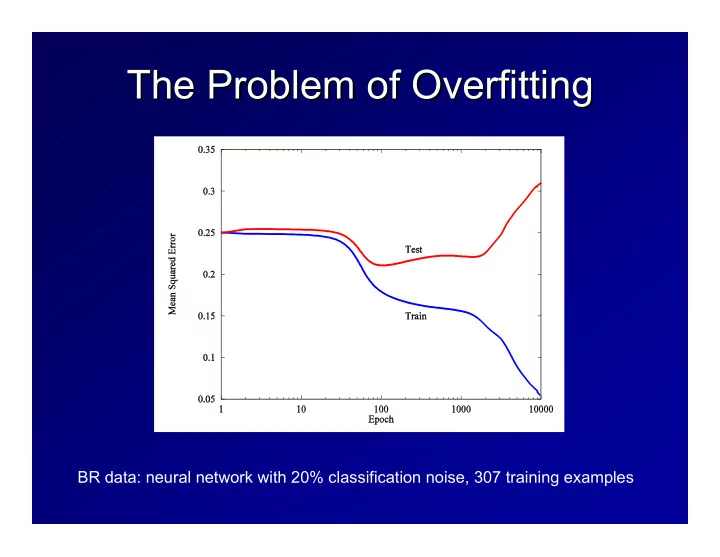

The Problem of Overfitting The Problem of Overfitting BR data: neural network with 20% classification noise, 307 training examples
Overfitting on BR (2) Overfitting on BR (2) Overfitting: h ∈ H overfits training set S if there exists H overfits training set S if there exists h ∈ H that H that Overfitting: h ∈ ’ ∈ h’ has higher training set error but lower test error on new data points. oints. has higher training set error but lower test error on new data p (More specifically, if learning algorithm A explicitly considers and and (More specifically, if learning algorithm A explicitly considers rejects h ’ in favor of in favor of h , we say that A has overfit the data.) rejects h , we say that A has overfit the data.) h’
Overfitting Overfitting H 1 ⊂ H 2 ⊂ H 3 ⊂ L If we use an hypothesis space H i that is too large, If we use an hypothesis space H i that is too large, eventually we can trivially fit the training data. In other eventually we can trivially fit the training data. In other words, the VC dimension will eventually be equal to the words, the VC dimension will eventually be equal to the size of our training sample m . size of our training sample m . This is sometimes called “ “model selection model selection” ”, because we , because we This is sometimes called can think of each H i as an alternative “ “model model” ” of the data of the data can think of each H i as an alternative
Approaches to Preventing Approaches to Preventing Overfitting Overfitting Penalty methods Penalty methods – MAP provides a penalty based on P(H) MAP provides a penalty based on P(H) – – Structural Risk Minimization Structural Risk Minimization – – Generalized Cross Generalized Cross- -validation validation – – Akaike Akaike’ ’s Information Criterion (AIC) s Information Criterion (AIC) – Holdout and Cross- -validation methods validation methods Holdout and Cross – Experimentally determine when overfitting occurs Experimentally determine when overfitting occurs – Ensembles Ensembles – Full Bayesian methods vote many hypotheses Full Bayesian methods vote many hypotheses – ∑ h ∑ P(y| x ,h) P(h|S) h P(y| x ,h) P(h|S) – Many practical ways of generating ensembles Many practical ways of generating ensembles –
Penalty methods Penalty methods Let ε ε train be our training set error and ε ε test be our test Let train be our training set error and test be our test ε test that minimizes ε error. Our real goal is to find the h h that minimizes . error. Our real goal is to find the test . ε test t directly evaluate ε The problem is that we can’ ’t directly evaluate . We The problem is that we can test . We ε train can measure ε , but it is optimistic can measure train , but it is optimistic Penalty methods attempt to find some penalty such that Penalty methods attempt to find some penalty such that ε test ε train ε = ε + penalty test = train + penalty The penalty term is also called a regularizer regularizer or or The penalty term is also called a regularization term. . regularization term During training, we set our objective function J to be During training, we set our objective function J to be ) = ε ε train J( w ( w ) + penalty( w ) J( w ) = train ( w ) + penalty( w ) and find the w w to minimize this function to minimize this function and find the
MAP penalties MAP penalties h map = argmax h P(S|h) P(h) h map = argmax h P(S|h) P(h) As h h becomes more complex, we can assign it a lower becomes more complex, we can assign it a lower As prior probability. A typical approach is to assign equal prior probability. A typical approach is to assign equal probability to each of the nested hypothesis spaces so probability to each of the nested hypothesis spaces so that that α = α P(h ∈ ∈ H H 1 ) = P(h ∈ ∈ H H 2 ) = L L = P(h 1 ) = P(h 2 ) = Because H 2 Because H 2 contains more hypotheses than H contains more hypotheses than H 1 1 , each , each individual h ∈ ∈ H H 2 will have lower prior probability: individual h 2 will have lower prior probability: ∑ i ∑ i α /|H P(h) = ∑ ) = ∑ i α P(h ∈ ∈ H H i /|H i | for each i where h ∈ ∈ H H i P(h) = i P(h i ) = i | for each i where h i If there are infinitely many H i , this will not work, because the probabilities must sum to 1. In this case, a common approach is P(h) = ∑ i 2 -i /|H i | for each i where h ∈ H i This is not usually a big enough penalty to prevent overfitting, however
Structural Risk Minimization Structural Risk Minimization Define regularization penalty using PAC theory Define regularization penalty using PAC theory " # T + 4 d k log 2 em + log 4 ² < = 2 ² k m d k δ " R 2 + k ξ k 2 # log 2 m + log 1 ² < = C γ 2 m δ
Other Penalty Methods Other Penalty Methods Generalized Cross Validation Generalized Cross Validation Akaike’ ’s Information Criterion s Information Criterion Akaike Mallow’ ’s P s P Mallow … …
Simple Holdout Method Simple Holdout Method Subdivide S into S train and S eval Subdivide S into S train and S eval For each H i , find h i ∈ H H i that best fits S train For each H i , find h i that best fits S i ∈ train Measure the error rate of each h i Measure the error rate of each h i on S on S eval eval Choose h i with the best error rate Choose h i with the best error rate Example: let H i be the set of neural network weights after i epochs of training on S train Our goal is to choose i
Simple Holdout Assessment Simple Holdout Assessment Advantages Advantages – Guaranteed to perform within a constant factor of any Guaranteed to perform within a constant factor of any – penalty method (Kearns, et al., 1995) penalty method (Kearns, et al., 1995) – Does not rely on theoretical approximations Does not rely on theoretical approximations – Disadvantages Disadvantages – S S train is smaller than S, so h h is likely to be less is likely to be less – train is smaller than S, so accurate accurate – If S – If S eval eval is too small, the error rate estimates will be is too small, the error rate estimates will be very noisy very noisy Simple Holdout is widely applied to make other Simple Holdout is widely applied to make other decisions such as learning rates, number of decisions such as learning rates, number of hidden units, SVM kernel parameters, relative hidden units, SVM kernel parameters, relative size of penalty, which features to include, feature size of penalty, which features to include, feature encoding methods, etc. encoding methods, etc.
k- -fold Cross fold Cross- -Validation to Validation to k determine H i determine H i Randomly divide S into k equal- -sized subsets sized subsets Randomly divide S into k equal Run learning algorithm k times, each time use Run learning algorithm k times, each time use one subset for S eval and the rest for S train one subset for S eval and the rest for S train Average the results Average the results
K- -fold Cross fold Cross- -Validation to determine H Validation to determine H i K i Partition S into K disjoint subsets S 1 , S 2 , … …, S , S k Partition S into K disjoint subsets S 1 , S 2 , k Repeat simple holdout assessment K times Repeat simple holdout assessment K times – In the In the k -th assessment, S th assessment, S train = S – – S S k and S eval = S k – k - train = S k and S eval = S k k be the best hypothesis from H – Let Let h be the best hypothesis from H i from iteration k. – ik i from iteration k. h i k over the K iterations Let ε ε i – Let be the average S eval of h over the K iterations – i be the average S eval of ik h i * = argmin ε i i ε – Let i Let i * = argmin i – i Train on S using H i and output the resulting Train on S using H * and output the resulting i* hypothesis hypothesis i i 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 1 1 2 2 k 3 3 k 4 4 5 5
Recommend
More recommend