TDDC17 So far: F 4 Today: Uninformed search Constraint - PowerPoint PPT Presentation

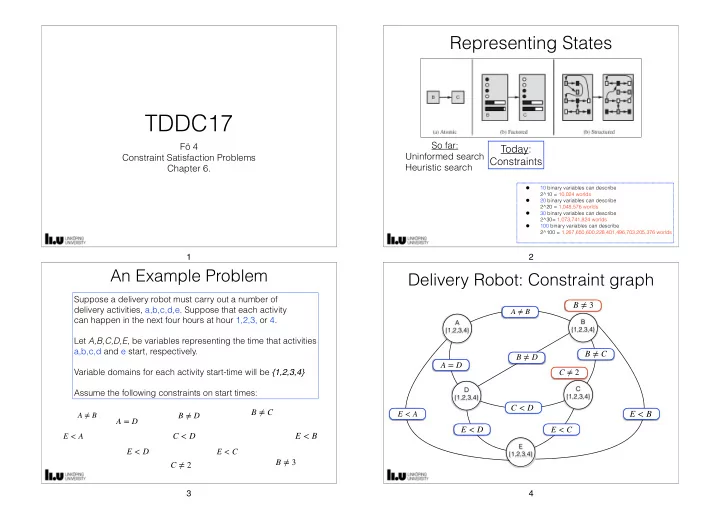
Representing States TDDC17 So far: Fö 4 Today: Uninformed search Constraint Satisfaction Problems Constraints Heuristic search Chapter 6. • 10 binary variables can describe 2^10 = 10,024 worlds • 20 binary variables can describe 2^20 = 1,048,576 worlds • 30 binary variables can describe 2^30= 1,073,741,824 worlds • 100 binary variables can describe 2^100 = 1,267,650,600,228,401,496,703,205,376 worlds 1 2 An Example Problem Delivery Robot: Constraint graph Suppose a delivery robot must carry out a number of B ≠ 3 delivery activities, a,b,c,d,e. Suppose that each activity A ≠ B can happen in the next four hours at hour 1,2,3, or 4. B A {1,2,3,4} {1,2,3,4} Let A,B,C,D,E , be variables representing the time that activities a,b,c,d and e start, respectively. B ≠ C B ≠ D A = D Variable domains for each activity start-time will be {1,2,3,4} C ≠ 2 C D Assume the following constraints on start times: {1,2,3,4} {1,2,3,4} C < D B ≠ C E < A E < B A ≠ B B ≠ D A = D E < D E < C E < B E < A C < D E E < D E < C {1,2,3,4} B ≠ 3 C ≠ 2 3 4

Constraint Satisfaction Problem Constraint Satisfaction Problem 𝒴 { X 1 , …, X n } is a set of variables, The constraints restrict the values variables can 𝒠 { D 1 , …, D n } is a set of domains, , one for each X i simultaneously take. 𝒟 { C 1 , …, C k } 𝒴 is a set of constraints, , on Solution to a CSP C i ∈ 𝒟 ⟨ scope , rel ⟩ Each constraint , consists of a pair , where An assignment of a value from its domain to each scope is a tuple of variables that participate in the constraint and variable, in such a way that all the constraints rel is a relation that defines the values those variables can take on. are satisfied Robot Delivery Example One may want to find 1 solution, all solutions, an optimal solution, or a good solution based on an objective function defined in terms of some or all variables. 𝒴 = { A , B , C , D , E } 𝒠 = {{1,2,3,4}, {1,2,3,4}, {1,2,3,4}, {1,2,3,4}, {1,2,3,4}} Solving a CSP is in general an NP Complete Problem! 𝒟 = { A ≠ B , A = D , B ≠ 3, B ≠ D , B ≠ C , C ≠ 2, C < D , E < A , E < D , E < C , E < B } ⟨ ( E , A ), E < A ⟩ or Constraint Example: ⟨ ( E , A ), {(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)} ⟩ 5 6 Delivery Robot: CSP Formulation Variable, Domain and Constraint Types Types of variables/domains RobD = CSP({'A':{1,2,3,4},'B':{1,2,3,4},'C':{1,2,3,4}, Some Special cases • Discrete variables 'D':{1,2,3,4}, 'E':{1,2,3,4}}, • Linear programming • Finite or infinite [Constraint((‘B',), ne_(3)), • Linear inequalities domains Constraint((‘C',), ne_(2)), forming a convex region. • Boolean variables Constraint((‘A','B'), ne), • Continuous domains: • Finite domain Constraint((‘B','C'), ne), • Solutions in time • (Continuous variables) Constraint((‘C','D'), lt), polynomial to the • Infinite domain Constraint((‘A','D'), eq), number of variables Constraint((‘A','E'), gt), • Integer programming Types of constraints Constraint((‘B','E'), gt), • Linear constraints on • Unary constraints (1) Constraint((‘C','E'), gt), integer variables. • Binary constraints (2) Constraint((‘D','E'), gt), • Higher-Order constraints (>2) Constraint((‘B','D'), ne)]) • Linear constraints Any higher-order/finite domain csp’s • Nonlinear constraints can be translated into binary/finite domain CSPs! (In the book, R/N stick to these) 7 8

Map Coloring Problem Let’s Abstract Constraint Graph Color each of the territories/states Nodes are variables red, green or blue with no neighboring region having the same color Arcs are constraints 9 10 Map Coloring: Australia Our Representation Map Coloring Specification Binary Constraints • Associate a variable with each region. 𝒴 = { WA , NT , SA , Q , NSW , V , T } • Introduce a set of WA ≠ NT • 𝒠 = {{ red , green , blue }, …{ red , green , blue }} values the variables can WA ≠ SA • be bound to. NT ≠ Q 𝒟 𝒴 • is a set of constraints on • Define constraints on NT ≠ SA • the variable/value pairs Q ≠ SA green • red Q ≠ NSW • red V ≠ SA • green V ≠ NSW • blue Goal: red CSP({‘WA':{'red','blue','green'},'NT':{'red','blue','green'}, ‘SA':{'red','blue','green'},'Q':{'red','blue','green'}, red 'NSW':{'red','blue','green'},'V':{'red','blue','green'}, Find a set of legal bindings 'T':{'red','blue','green'}}, [Constraint(('WA','NT'),ne),Constraint(('WA','SA'),ne), satisfying the constraints! Constraint(('NT','SA'),ne),Constraint(('NT','Q'),ne), Constraint((‘SA','Q'),ne),Constraint(('SA','NSW'),ne), Constraint((‘SA’,’V’),ne), Constraint((‘Q’,’NSW'),ne) ]) 11 12

Sudoku Another Example 𝒲 = { A 1,… A 9,…, I 1,…, I 9} 81 variables For empty squares: • Suppose our territories are coverage areas, each with a 𝒠 ( A 1) = {1,2,3,4,5,6,7,8,9} sensor that monitors the area. For pre-filled squares: • Each sensor has N possible radio frequencies 𝒠 ( A 3) = {3}, … 𝒠 ( I 7) = {3} • Sensors overlap if they are in adjacent areas No digit should appear twice • If sensors overlap, they can not use the same frequency in any row, column, or unit 27 alldiff () constraints one for each row, column and 9 cell area: Find a solution where each sensor uses a frequency alldiff ( A 1, A 2, A 3, A 4, A 5, A 6, A 7, A 8, A 9} that does not interfere with sensors in adjacent coverage areas alldiff ( A 3, B 3, C 3, D 3, E 3, F 3, G 3, H 3, I 3} alldiff ( A 4, A 5, A 6, B 4, B 5, B 6, C 4, C 5, C 6} This is an N-color problem on coverage areas! Sudoku games have exactly one solution! 13 14 Solving a CSP: Types of Algorithms Advantages of CSPs Inference Search Constraint Propagation • Representation is closer to the original problem. (reduce the # of legal values for a (choose a new variable assignment ) variable and propagate to other • Representation is the same for all constraint problems. variables) • Algorithms used are domain independent with the same general purpose heuristics for all problems Constraint • Algorithms are simple and often find solutions quite rapidly for large Constraint Constraint problems Propagation Propagation Propagation • CSPs often more efficient than regular state-space search Pre-Processing because it can quickly eliminate large parts of the search space Sometimes solves Interleave the problem • Many problems intractable for regular state-space search can without search! be solved efficiently with a CSP formulation. Search Search 15 16

Backtracking Algorithm (Search with Inference) Simple Backtracking Search Algorithm for CSPs Algorithm is based on recursive depth-first search Domain Independent Heuristics Inference Forward Checking Arc-consistency If a value assignment to a variable leads to Path Consistency failure then it is removed from the current K-Consistency assignment and a new value is tried (backtrack) The algorithm we focus on will interleave inference with search 17 18 Backtracking Algorithm (Search with Inference) Potential Problems with generic backtracking search def backtrack_search_constraints (cspproblem): Python • Variable choice and value assignment is arbitrary Program def backtrack (assignment,cspproblem): • Which variable should be assigned? if assignment.complete(cspproblem): return assignment • SELECT-UNASSIGNED-VARIABLE() var = select_unassigned_variable(cspproblem,assignment) for value in order_domain_values(var,assignment,cspproblem): • Which values should be assigned first? if assignment.consistent_with(var,value, cspproblem): assignment.add(var,value) • ORDER-DOMAIN-VALUES() infer = inferences(cspproblem,var,assignment) if not infer == 'failure': • Conflicts detected too late (empty value domain) assignment.add_inferences(infer) result = backtrack (assignment, cspproblem) • Conflicts not detected until they actually occur. if not result == 'failure': return result • What are the implications of current variable assignments for the other unassigned variables? assignment.remove(var,value) assignment.remove_inferences(infer) • INFERENCE() return 'failure' • Thrashing b_s_f calls: return backtrack(assignment(),cspproblem) • Major reason for failure is conflicting variables, but these conflicts are continually repeated Domain Independent def select_unassigned_variable (cspproblem,assignment): throughout the search return assignment.unassigned_variables(cspproblem)[0] Heuristics • When a path fails, can the search avoid repeating the failure in subsequent paths? def inferences (cspproblem,var,assignment): Need to instantiate! return {} • One solution: Intelligent Backtracking def order_domain_values (var,assignment,cspproblem): return list(cspproblem.domains[var]) 19 20