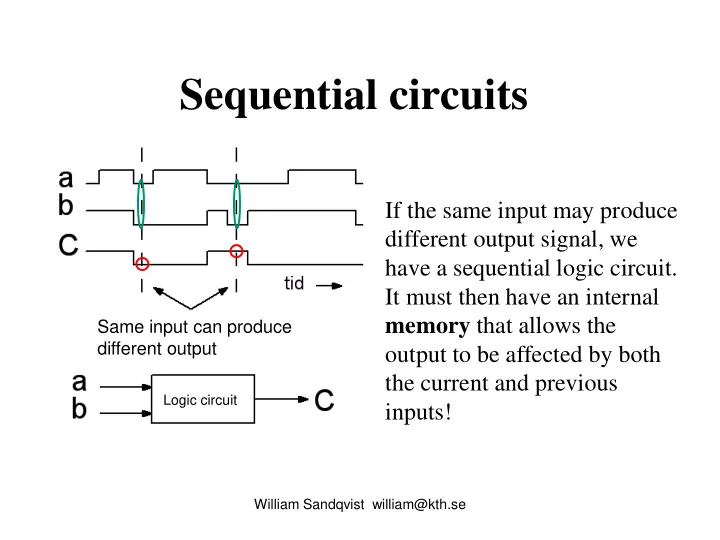

Sequential circuits If the same input may produce different output signal, we have a sequential logic circuit. It must then have an internal memory that allows the Same input can produce different output output to be affected by both the current and previous Logic circuit inputs! William Sandqvist william@kth.se
Moore-machine State NEXT STATE OUTPUT STATE REGISTER DECODER DECODER Input- Output- signals signals Clk For Moore machine the outputs depends on the inputs and the internal state. The internal memory is the state register consisting of D flip-flops. William Sandqvist william@kth.se
State register D-flip-flops State register D flip-flops slows down the race between signals until the value is stable. (Compare with the tollbooth). Input- signals Output- NEXT STATE STATE OUTPUT DECODER signals REGISTER DECODER William Sandqvist william@kth.se
State register D-flip-flops State register D flip-flops slows down the race between signals until the value is stable. (Compare with the tollbooth). ? Input- signals Output- NEXT STATE STATE OUTPUT DECODER signals REGISTER DECODER ? William Sandqvist william@kth.se
State register D-flip-flops State register D flip-flops slows down the race between signals until the value is stable. (Compare with the tollbooth). ! ? Input- signals Output- NEXT STATE STATE OUTPUT DECODER signals REGISTER DECODER ? ! William Sandqvist william@kth.se
Quickie Question … flip-flop Which of the following timing diagram is valid for a edge-triggered D flip-flop? In1 Out Q D In2 Clock In1 In1 In1 In2 In2 In2 Out Out Out Alt: A Alt: B Alt: C William Sandqvist william@kth.se
Quickie Question … flip-flop Which of the following timing diagram is valid for a edge-triggered D flip-flop? In1 Out Q D In2 Clock In1 In1 In1 In2 In2 In2 Out Out Out Alt: A Alt: B Alt: C D is copied to output at the edge, when Clock goes from 0 to 1 William Sandqvist william@kth.se
Quickie Question … Latch Which of the following timing diagram is valid for a D Latch? In1 Out Q D In2 Enable In1 In1 In1 In2 In2 In2 Out Out Out Alt: A Alt: B Alt: C William Sandqvist william@kth.se
Quickie Question … Latch Which of the following timing diagram is valid for a D Latch? In1 Out Q D In2 Enable In1 In1 In1 In2 In2 In2 Out Out Out Alt: A Alt: B Alt: C D is connected to output when Enable is 1, and is locked when Enable is 0 William Sandqvist william@kth.se
Design: ”two consecutive” Sequence Detector. If w has been 1 in two w z w (or more) consecutive clock then z = 1. (Reset) Clk C Specification Sequence circuit has an input w and an output z If input w has been 1 in during the current and previous clock cycle then z will be set to 1 Use a Moore machine with D-flip-flops to realizing the design. William Sandqvist william@kth.se
Statediagram ”two consecutive” Reset State w = 1 ⁄ ⁄ w = 0 A z 0 = B z 0 = w = 0 State transition A zero w = 0 w = 1 B single one C two or moore consecutive ⁄ C z 1 = State name Output value w = 1 William Sandqvist william@kth.se
State table Next state Present Output state z w = 0 w = 1 A A B 0 B A C 0 C A C 1 Three states – two flip-flops needed to hold state numbers! William Sandqvist william@kth.se
”two consecutive” as Moore- machine Y y 1 1 w Combinational Combinational z circuit circuit Y y 2 2 Clock William Sandqvist william@kth.se
Designdecissions • The designer must decide which flip-flops? to be used D-, T-, or JK-flip-flop • The designer must choose the code for each state William Sandqvist william@kth.se
Designbeslut This time: • D-flip-flop • State code A = 00, B = 01, C = 10 • The code word 11 should not occur. We choose don’t care. William Sandqvist william@kth.se
Coded state table Next state Present w = 0 w = 1 Output state z y 2 y Y 2 Y Y 2 Y 1 1 1 A = 00 A 00 00 01 0 B = 01 01 00 10 B 0 C = 10 C 10 00 10 1 11 dd dd d = = Y Y f y y w ( ) z f y y ( ) 2 1 2 1 2 1 William Sandqvist william@kth.se
Next state decoder The Next state decoder consists of two logic networks available as input network to the two flip-flops. In order to minimize logic networks, we enter the truth tables in the form of Karnaugh maps. = = = Y Y f ( y y w ) Y f ( y y w ) Y f ( y y w ) 2 1 2 1 2 2 1 1 2 1 = z f ( y y ) 2 1 William Sandqvist william@kth.se
From coded statetable to Karnaughmap = = = ( ) ( ) ( ) Y Y f y y w Y f y y w Y f y y w 2 1 2 1 2 2 1 1 2 1 y y Y 2 1 1 00 01 11 10 w 1 = wy 0 0 0 d 0 Y 1 y 2 1 1 0 d 0 y y Y 2 1 2 w 00 01 11 10 = + = Y wy wy 0 0 0 d 0 2 1 2 = + w ( y y ) 1 0 1 d 1 1 2 William Sandqvist william@kth.se
Output decoder z = f ( y 2 y ) 1 y 1 y 2 0 1 z = y 2 0 0 0 1 1 d William Sandqvist william@kth.se
Implementation = + = Y wy wy 2 1 2 = + w ( y y ) 1 2 1 = wy Y 1 y 2 z = y 2 William Sandqvist william@kth.se
Timing diagram ”two consecutive” t t t t t t t t t t t 0 1 2 3 4 5 6 7 8 9 10 1 Clock 0 1 w State 0 transitions 1 y occurs only on 1 0 the positive 1 y clock edge! 2 0 1 z 0 William Sandqvist william@kth.se
In other terms Present state Next state + y y Exercises and Hemert-book: + + + + = = = y y f ( y y w ) y f ( y y w ) y f ( y y w ) 2 1 2 1 2 2 1 1 2 1 William Sandqvist william@kth.se
With another lineup + + + + = = = y y f ( y y w ) y f ( y y w ) y f ( y y w ) 2 1 2 1 2 2 1 1 2 1 A B In exercises C we use this method You could directly write down the codet state table as a ”Karnaugh map”. William Sandqvist william@kth.se
William Sandqvist william@kth.se
Mealy-machine State NEXT STATE OUTPUT STATE REGISTER DECODER DECODER Input- Output- signals signals Clk In a Mealy Machine output signals depends on both the current state and the inputs. William Sandqvist william@kth.se
State diagram Mealy ”Two consecutive” • The state diagram for the Mealy-machine only needs two states • Output signal depends booth on states and input. Reset ⁄ Value of input signal w 1 = z 0 = ⁄ ⁄ w 0 = z 0 = w 1 = z 1 = A B ⁄ Value of output signal w 0 = z 0 = State name William Sandqvist william@kth.se
State table Reset ⁄ w 1 = z 0 = ⁄ ⁄ w 0 = z 0 = w 1 = z 1 = A B ⁄ w 0 = z 0 = Next state Output z Present state w = 0 w = 1 w = 0 w = 1 A A B 0 0 B A B 0 1 Two states – only one flip-flop is needed! William Sandqvist william@kth.se
Coded state table = = Y f ( y w ) z f ( y w ) Next state Output Present state w = 0 w = 1 w = 0 w = 1 y Y Y z z A = 0 A 0 0 1 0 0 B = 1 B 1 0 1 0 1 = = Y w z yw Directly from the table: William Sandqvist william@kth.se
Implementation z w D Q y Clock Q Resetn William Sandqvist william@kth.se
Timing diagram • The output may change during the clock period, since it is a function of the input signal • Compared to Moore machine the Mealy machine is moore 'responsive' (bit sequence is detected in t 4 compared to t 5 for the Moore-machine) t t t t t t t t t t t 0 1 2 3 4 5 6 7 8 9 10 1 Clock 0 1 w 0 1 y 0 1 z 0 William Sandqvist william@kth.se
Mealy with output register • The disadvantage of the Mealy machine is that the output can be changed during the entire clock period • You can add a register (flip-flop) at the end so to synchronize the output with the clock edge z D Q Z w Q D Q y Q Clock Resetn William Sandqvist william@kth.se
Timing diagram with output register With an output register there are no longer any differences between the timing diagrams! t t t t t t t t t t t 0 1 2 3 4 5 6 7 8 9 10 1 Clock 0 1 w 0 1 y 0 1 z 0 1 Z 0 William Sandqvist william@kth.se
Moore vs Mealy • Moore- machine output values depend only on the current state • Mealy- machine output values depend on the current state and the values of the input signals • Mealy-machine often uses fewer states • Mealy-machine output signals are not inte synchronized with the clock, why you often has to add an output register William Sandqvist william@kth.se
William Sandqvist william@kth.se
Selection of state encoding Selection of state encoding can play a major role in implementation as it affects the logic for • Next-state-decoder • Output decoder William Sandqvist william@kth.se
”two consecutive” state diagram Reset w = 1 ⁄ ⁄ w = 0 A z 0 = B z 0 = w = 0 w = 1 w = 0 ⁄ C z 1 = w = 1 William Sandqvist william@kth.se
State code = Binary Next state Present w = 0 w = 1 Output state z y y Y Y Y Y 2 1 2 1 2 1 A = 00 A 00 00 01 0 B = 01 01 00 10 B 0 C = 10 C 10 00 10 1 11 11 dd dd d William Sandqvist william@kth.se
Realization (Binary code) 2 D-flip-flops 2 AND-gates 1 OR-gate William Sandqvist william@kth.se
Recommend
More recommend