S " # Context-Free Pushdown Grammars Automata A derivation: - PowerPoint PPT Presentation
Plan for This Today Our Next Class of Languages Context Free Grammars model for specifying programming languages Context-Free Languages why not just use regular expressions? example grammar derivations R n b n { ww } { a }
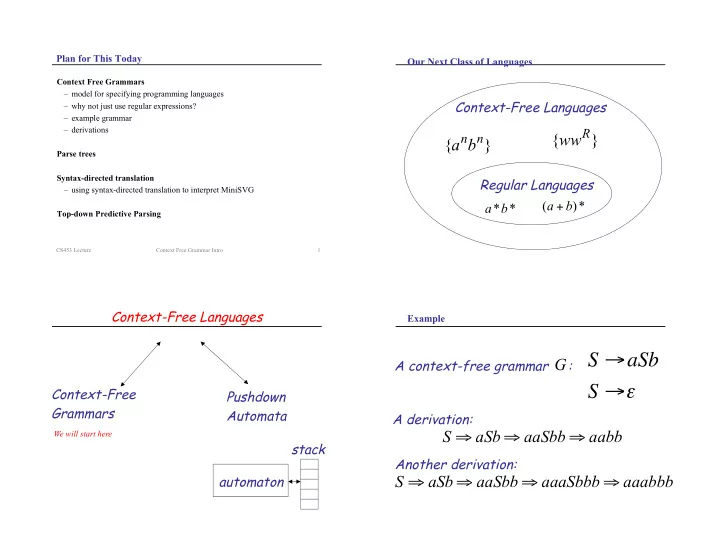
Plan for This Today Our Next Class of Languages Context Free Grammars – model for specifying programming languages Context-Free Languages – why not just use regular expressions? – example grammar – derivations R n b n { ww } { a } Parse trees Syntax-directed translation Regular Languages – using syntax-directed translation to interpret MiniSVG ( a + b ) * a * b * Top-down Predictive Parsing CS453 Lecture Context Free Grammar Intro 1 Context-Free Languages Example A context-free grammar : S " aSb G S " # Context-Free Pushdown Grammars Automata A derivation: S aSb aaSbb aabb We will start here ! ! ! stack Another derivation: automaton S aSb aaSbb aaaSbbb aaabbb ! ! ! !
An Application of This Language Deriving another grammar S aSb " Context-Free Languages S " ! Gave a Can we derive a grammar n b n Grammar for: { a } R for: { ww } n n L ( G ) { a b : n 0 } = ! Regular Languages (((( )))) Describes parentheses: Representing All Properly Nested Example Parentheses A context-free grammar : G S " aSa S aSb " S " bSb S " ! S " # A derivation: n n L ( G ) { a b : n 0 } = ! S aSa abSba abba ! ! ! (((( )))) Another derivation: Describes parentheses: S aSa abSba abaSaba abaaba ! ! ! ! Can we build a grammar to include any valid combination of ()? For example ( () (()) )
The Possible Grammar Context-Free Grammars S " ( S ) A context-free grammar : G Grammar G = ( V , T , S , P ) S " SS Nonterminals Terminals Start S " # symbol A derivation: S " SS " ( S ) S " () S " () Productions of the form: Another derivation: A ! x Nonterminal String of symbols, S " SS " ( S ) S " () S " ()( S ) " ()() Nonterminals and terminals Derivation Order Derivation Order Given a grammar with rules: Given a grammar with rules: 1 . S ! AB 2. A " aaA 1 . S ! AB 2. A " aaA 4. B " Bb 4. B " Bb 3. A " # 3. A " # 5. B " # 5. B " # Always expand the leftmost non-terminal Always expand the rightmost non-terminal Leftmost derivation: 1 2 3 4 5 Rightmost derivation: S AB aaAB aaB aaBb aab ! ! ! ! ! 1 4 5 2 3 S AB ABb Ab aaAb aab ! ! ! ! !
Grammar String Parse Trees S ! AB A " aaA | # B " Bb | # Stm --> id := Exp a := ( b := ( c := 3, 2 ), 1 ) Exp --> num Exp --> ( Stm, Exp ) S ! AB Leftmost derivation: S Stm ==> a := Exp ==> a := ( Stm, Exp ) ==> a := ( b := Exp, Exp ) ==> a := ( b := ( Stm, Exp ), Exp ) ==> a := ( b := ( c := Exp, Exp ), Exp ) ==> a := ( b := ( c := 3, Exp ), Exp ) ==> a := ( b := ( c := 3, 2), Exp ) ==> a := ( b := ( c := 3, 2), 1) A B Rightmost derivation: Stm ==> a := Exp ==> a := ( Stm, Exp ) ==> a := ( Stm, 1) ==> Parse Trees Parse Trees S ! AB S ! AB A " aaA | # B " Bb | # A " aaA | # B " Bb | # S AB aaAB S AB aaAB aaABb ! ! ! ! ! S S A B A B a a A a a A B b
Parse Trees Parse Trees S ! AB S ! AB A " aaA | # B " Bb | # A " aaA | # B " Bb | # S AB aaAB aaABb aaBb S AB aaAB aaABb aaBb aab ! ! ! ! ! ! ! ! ! S S A B A B yield aa "" b a a A B b a a A B b = aab " " " Sentential forms S ! AB A " aaA | # B " Bb | # S AB aaAB sentential ! ! form Partial parse tree S S ! AB A B Partial parse tree S a a A A B
Sometimes, derivation order doesn’t matter Does it matter here? Parse Tree Leftmost: S AB aaAB aaB aaBb aab ! ! ! ! ! Grammar Stm --> id := Exp Rightmost: Exp --> num Exp --> ( Stm, Exp ) S AB ABb Ab aaAb aab ! ! ! ! ! String S Same parse tree a := ( b := ( c := 3, 2 ), 1 ) A B a a A B b " " CS453 Lecture Context Free Grammar Intro 22 How about here? Syntax Directed Translation or Interpretation Use parse tree to … Grammar – Translate one language to another (1) exp --> exp * exp – Create a data structure of the program (2) exp --> exp + exp – Interpret, or evaluate, the program (3) exp --> NUM Works conceptually by… String – Parser discovers the parse tree – Parser executes certain actions while “traversing” the parse tree using a 42 + 7 * 6 depth-first, post-order traversal CS453 Lecture Context Free Grammar Intro 23 CS453 Lecture Context Free Grammar Intro 24
MiniSVG Grammar Example Parse Tree for MiniSVG svg -> SVG_START elem_list SVG_END elem_list -> elem elem_list | epsilon elem -> RECT_START KW_X EQ NUM KW_Y EQ NUM KW_WIDTH EQ NUM KW_HEIGHT EQ NUM KW_FILL EQ COLOR ELEM_END | CIRCLE_START KW_CX EQ NUM KW_CY EQ NUM KW_R EQ NUM KW_FILL EQ COLOR ELEM_END | LINE_START KW_X1 EQ NUM KW_Y1 EQ NUM KW_X2 EQ NUM KW_Y2 EQ NUM KW_STROKE EQ COLOR ELEM_END CS453 Lecture Context Free Grammar Intro 25 CS453 Lecture Context Free Grammar Intro 26 Interpret this program How about here? Parse Tree Grammar Grammar Stm --> id := Exp (1) exp --> exp * exp Exp --> num (2) exp --> exp + exp Exp --> ( Stm, Exp ) (3) exp --> NUM String String a := ( b := ( c := 3, 2 ), 1 ) 42 + 7 * 6 CS453 Lecture Context Free Grammar Intro 27 CS453 Lecture Context Free Grammar Intro 28
Example: Parser Parser derivation input S " SS derivation input grammar string S " aSb aabb ? S " bSa S "# Exhaustive Search S " SS | aSb | bSa | # Phase 1: Find derivation of S " SS S " SS aabb aabb S " aSb S " aSb S " bSa S " bSa S " # S " # All possible derivations of length 1
Phase 2 S " SS | aSb | bSa | # S " SS | aSb | bSa | # Phase 2 S SS SSS S SS SSS ! ! ! ! S SS aSbS aabb aabb S SS aSbS ! ! ! ! Phase 1 S SS bSaS S SS S ! ! ! ! S SS S SS S ! ! ! S aSb aSSb ! ! S aSb ! S aSb aSSb ! ! S aSb aaSbb ! ! S aSb aaSbb ! ! Phase 3 S aSb abSab ! ! S aSb aaSbb aabb ! ! ! S aSb ab ! ! Final result of exhaustive search Time complexity of exhaustive search (top-down parsing) Parser Suppose there are no productions of the form S " SS input A "# S " aSb aabb S " bSa A ! B S " # 2 w | | Number of phases for string : w derivation S aSb aaSbb aabb ! ! !
For grammar with rules k 2 Time for phase 1: k Time for phase 2: k 2 k possible derivations possible derivations k Total time needed for string : w 2 w | | Time for phase : 2 w | | k 2 2 | w | k k ! k + + + 2 w | | possible derivations k phase 1 phase 2|w| phase 2 Extremely bad!!!
For general context-free grammars: Example Predictive Parser (1) start -> mesh EOF (2) mesh -> NUM nodelist NUM elemlist (3a & b) nodelist -> ϵ | node nodelist There exists a parsing algorithm (4) node -> NODE NUM REAL REAL // node_id, x, y (5a & b) elemlist -> ϵ | elem elemlist that parses a string | w | (6a) elem -> TRI NUM NUM NUM NUM // elem_id, 3 node ids (6b) elem -> SQR NUM NUM NUM NUM NUM //elem_id,4 node ids 3 in time | w | void start() { switch(m_lookahead) { case NUM: mesh(); match(Token.Tag.EOF); break; default: throw new ParseException(…); }} void mesh() { switch(this.m_lookahead) { case NUM: num_nodes = ((Num)m_lookahead).value; match(NUM); nodelist(); For LL(1) grammars we can use num_elem = ((Num)m_lookahead).value; match(NUM); elemlist(); break; default: throw new ParseException(…); Predictive parsing and parse in | | w }} void nodelist() { switch(m_lookahead) { case NUM: break; // nodelist -> epsilon case NODE: node(); nodelist(); break; // nodelist -> node nodelist default: throw new ParseException(…); }} CS453 Lecture Context Free Grammar Intro 42 CS453 Lecture Context Free Grammar Intro 43
Recommend
More recommend
Explore More Topics
Stay informed with curated content and fresh updates.























