Reporting bullying A recent SurveyUSA poll conducted in FL asked - PowerPoint PPT Presentation

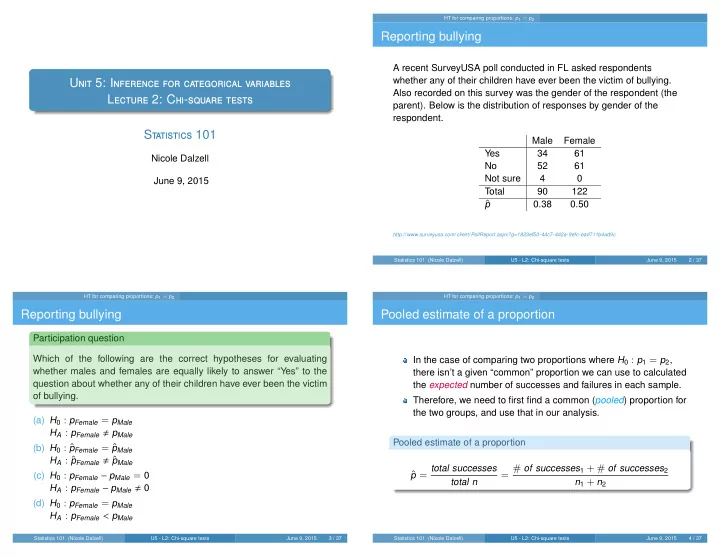
HT for comparing proportions: p 1 = p 2 Reporting bullying A recent SurveyUSA poll conducted in FL asked respondents whether any of their children have ever been the victim of bullying. U  5: I     Also recorded on this survey was the gender of the respondent (the L  2: C  -   parent). Below is the distribution of responses by gender of the respondent. S  101 Male Female Yes 34 61 Nicole Dalzell No 52 61 Not sure 4 0 June 9, 2015 Total 90 122 ˆ p 0.38 0.50 http://www.surveyusa.com/client/PollReport.aspx?g=1823ef50-44c7-4d2a-9efc-ead711b4ad9c Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 2 / 37 HT for comparing proportions: p 1 = p 2 HT for comparing proportions: p 1 = p 2 Reporting bullying Pooled estimate of a proportion Participation question Which of the following are the correct hypotheses for evaluating In the case of comparing two proportions where H 0 : p 1 = p 2 , whether males and females are equally likely to answer “Yes” to the there isn’t a given “common” proportion we can use to calculated question about whether any of their children have ever been the victim the expected number of successes and failures in each sample. of bullying. Therefore, we need to first find a common ( pooled ) proportion for the two groups, and use that in our analysis. (a) H 0 : p Female = p Male H A : p Female � p Male Pooled estimate of a proportion (b) H 0 : ˆ p Female = ˆ p Male H A : ˆ p Female � ˆ p Male p = total successes = # of successes 1 + # of successes 2 ˆ (c) H 0 : p Female − p Male = 0 total n n 1 + n 2 H A : p Female − p Male � 0 (d) H 0 : p Female = p Male H A : p Female < p Male Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 3 / 37 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 4 / 37

HT for comparing proportions: p 1 = p 2 HT for comparing proportions: p 1 = p 2 Application exercise: Pooled proportion Application exercise: HT for comparing proportions Calculate the estimated pooled proportion of males and females who Conduct a hypothesis test, at 5% significance level, to determine if said that one of their children has been a victim of bullying. Which males and females are equally likely to answer “Yes” to the question sample proportion ( ˆ p Female or ˆ p Male ) the pooled estimate is closer to? about whether any of their children have ever been the victim of bully- Why? ing. Male Female Male Female Yes 34 61 Yes 34 61 No 52 61 No 52 61 Not sure 4 0 Not sure 4 0 Total 90 122 Total 90 122 p ˆ 0.38 0.50 ˆ p 0.38 0.50 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 5 / 37 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 6 / 37 HT for comparing proportions: p 1 = p 2 Recap Recap - inference for one proportion Population parameter: p , point estimate: ˆ p Conditions: independence - random sample and 10% condition at least 10 successes and failures - if not → randomization � p ( 1 − p ) Standard error: SE = n for CI: use ˆ p for HT: use p 0 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 7 / 37 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 8 / 37

Recap Recap Recap - comparing two proportions Reference - standard error calculations one sample two samples Population parameter: ( p 1 − p 2 ) , point estimate: (ˆ p 1 − ˆ p 2 ) Conditions: � s 2 s 2 s mean SE = SE = n 1 + 1 2 √ n independence within groups n 2 - random sample and 10% condition met for both groups independence between groups at least 10 successes and failures in each group � � p ( 1 − p ) p 1 ( 1 − p 1 ) + p 2 ( 1 − p 2 ) SE = SE = proportion - if not → randomization n n 1 n 2 � p 1 ( 1 − p 1 ) + p 2 ( 1 − p 2 ) p 2 ) = SE (ˆ p 1 − ˆ n 1 n 2 for CI: use ˆ p 1 and ˆ p 2 When working with means, it’s very rare that σ is known, so we for HT: usually use s . p pool = # suc 1 +# suc 2 when H 0 : p 1 = p 2 : use ˆ n 1 + n 2 when H 0 : p 1 − p 2 = (some value other than 0) : use ˆ p 1 and ˆ p 2 When working with proportions, - this is pretty rare if doing a hypothesis test, p comes from the null hypothesis if constructing a confidence interval, use ˆ p instead Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 9 / 37 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 10 / 37 Chi square test of GOF Chi square test of GOF Jury selection – random or not? Categorical Data Jury selection In a county where jury selection is supposed to be random, a civil rights group sues the county, claiming racial disparities in jury selection. Ethnicities of the people in the county who are eligible for jury We have been working with proportions and differences in duty is as follows (based on census results): proportions. Ethnicity White Black Nat. Amer. Asian & PI Other % in pop. 80.29% 12.06% 0.79% 2.92% 3.94% What do we do if our categorical variable has more than two levels? The previous year, 2500 people were selected for jury duty; their Let’s see an example. ethnicities were as follows: Ethnicity White Black Nat. Amer Asian & PI Other jurors selected 1920 347 19 84 130 The court retains you as an independent expert to assess the statistical evidence that there was discrimination. You propose to formulate the issue as an hypothesis test. Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 11 / 37 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 12 / 37

Chi square test of GOF Jury selection – random or not? Chi square test of GOF Jury selection – random or not? Setting the hypotheses Evaluating the hypotheses As we are used to doing, we take a look at what the universe looks like under the null hypothesis. In this universe in which “the observed counts of jurors from various race/ethnicities follow the same ethnicity distribution in the population”, what do we expect our observed counts to be? What should the hypotheses be? To evaluate these hypotheses, we quantify how different the Remember: H 0 always says “there’s nothing going on”. observed counts are from the expected counts. In other words, how different is our observed counts from what we should be seeing if the null hypothesis were true? Large deviations from what would be expected based on sampling variation (chance) alone provide strong evidence for the alternative hypothesis. This is called a goodness of fit test since we’re evaluating how well the observed data fit the expected distribution. Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 13 / 37 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 14 / 37 Chi square test of GOF Jury selection – random or not? Chi square test of GOF The chi-square test statistic Anatomy of a test statistic Application exercise: Expected counts in one-way tables The general form of a test statistic is Calculate expected number of jurors from each ethnicity if in fact the jury selection is random. point estimate − null value n = 2500 SE of point estimate This construction is based on Ethnicity White Black Nat. Amer. Asian & PI Other identifying the difference between a point estimate and an 1 % in pop. 80.29% 12.06% 0.79% 2.92% 3.94% expected value if the null hypothesis was true, and Observed Counts 1920 347 19 84 130 standardizing that difference using the standard error of the point 2 estimate. These two ideas will help in the construction of an appropriate test statistic for count data. Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 15 / 37 Statistics 101 (Nicole Dalzell) U5 - L2: Chi-square tests June 9, 2015 16 / 37