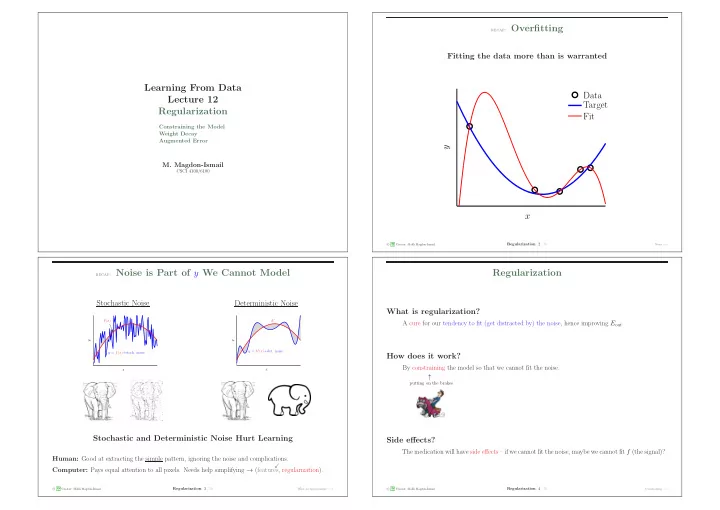

recap: Overfitting Fitting the data more than is warranted Learning From Data Data Lecture 12 Target Regularization Fit Constraining the Model Weight Decay Augmented Error y M. Magdon-Ismail CSCI 4100/6100 x � A M Regularization : 2 /30 c L Creator: Malik Magdon-Ismail Noise − → recap: Noise is Part of y We Cannot Model Regularization Stochastic Noise Deterministic Noise What is regularization? f ( x ) h ∗ A cure for our tendency to fit (get distracted by) the noise, hence improving E out . y y y = h ∗ ( x )+det. noise y = f ( x )+stoch. noise How does it work? By constraining the model so that we cannot fit the noise. x x ↑ putting on the brakes Stochastic and Deterministic Noise Hurt Learning Side effects? The medication will have side effects – if we cannot fit the noise, maybe we cannot fit f (the signal)? Human: Good at extracting the simple pattern, ignoring the noise and complications. � Computer: Pays equal attention to all pixels. Needs help simplifying → (features , regularization). � A c M Regularization : 3 /30 � A c M Regularization : 4 /30 L Creator: Malik Magdon-Ismail What is regularization? − → L Creator: Malik Magdon-Ismail Constraining − →
Constraining the Model: Does it Help? Constraining the Model: Does it Help? y y y x x x constrain weights to be smaller . . . and the winner is: . . . and the winner is: � A M Regularization : 5 /30 � A M Regularization : 6 /30 c L Creator: Malik Magdon-Ismail Small weights − → c L Creator: Malik Magdon-Ismail bias − → Bias Goes Up A Little Variance Drop is Dramatic! ¯ g ( x ) ¯ g ( x ) g ( x ) ¯ g ( x ) ¯ y y y y sin( x ) sin( x ) sin( x ) sin( x ) x x x x no regularization regularization no regularization regularization bias = 0 . 21 bias = 0 . 23 bias = 0 . 21 bias = 0 . 23 ← side effect ← side effect var = 1 . 69 var = 0 . 33 ← treatment (Constant model had bias =0.5 and var =0.25.) (Constant model had bias =0.5 and var =0.25.) � A c M Regularization : 7 /30 � A c M Regularization : 8 /30 L Creator: Malik Magdon-Ismail var − → L Creator: Malik Magdon-Ismail Regularication in a nutshell − →
Regularization in a Nutshell Polynomials of Order Q - A Useful Testbed H q : polynomials of order Q . VC analysis: Standard Polynomial Legendre Polynomial E out ( g ) ≤ E in ( g ) + Ω( H ) we’re using linear regression տ ւ 1 1 If you use a simpler H and get a good fit, x L 1 ( x ) h ( x ) = w t z ( x ) then your E out is better. h ( x ) = w t z ( x ) x 2 z = L 2 ( x ) z = . = w 0 + w 1 x + · · · + w q x q . . = w 0 + w 1 L 1 ( x ) + · · · + w q L q ( x ) . . . տ x q L q ( x ) allows us to treat the weights ‘independently’ Regularization takes this a step further: If you use a ‘simpler’ h and get a L 1 L 2 L 3 L 4 L 5 good fit, then is your E out better? 2 (3 x 2 − 1) 2 (5 x 3 − 3 x ) 8 (35 x 4 − 30 x 2 + 3) 8 (63 x 5 · · · ) 1 1 1 1 x � A M Regularization : 9 /30 � A M Regularization : 10 /30 c L Creator: Malik Magdon-Ismail Polynomials − → c L Creator: Malik Magdon-Ismail recap: linear regression − → Constraining The Model: H 10 vs. H 2 recap: Linear Regression − → ( x 1 , y 1 ) , . . . , ( x N , y N ) ( z 1 , y 1 ) , . . . , ( z N , y N ) � � H 10 = h ( x ) = w 0 + w 1 Φ 1 ( x ) + w 2 Φ 2 ( x ) + w 3 Φ 3 ( x ) + · · · + w 10 Φ 10 ( x ) � �� � � �� � X y Z y N min : E in ( w ) = 1 � ( w t z n − y n ) 2 N n =1 � h ( x ) = w 0 + w 1 Φ 1 ( x ) + w 2 Φ 2 ( x ) + w 3 Φ 3 ( x ) + · · · + w 10 Φ 10 ( x ) � = 1 N (Z w − y ) t (Z w − y ) H 2 = such that: w 3 = w 4 = · · · = w 10 = 0 ր a ‘hard’ order constraint that sets some weights to zero w lin = (Z t Z) − 1 Z t y ր linear regression fit H 2 ⊂ H 10 � A c M Regularization : 11 /30 � A c M Regularization : 12 /30 L Creator: Malik Magdon-Ismail Already saw constraints − → L Creator: Malik Magdon-Ismail Soft constraint − →
Soft Order Constrained Model H C Soft Order Constraint � � H 10 = h ( x ) = w 0 + w 1 Φ 1 ( x ) + w 2 Φ 2 ( x ) + w 3 Φ 3 ( x ) + · · · + w 10 Φ 10 ( x ) Don’t set weights explicitly to zero (e.g. w 3 = 0). Give a budget and let the learning choose. � h ( x ) = w 0 + w 1 Φ 1 ( x ) + w 2 Φ 2 ( x ) + w 3 Φ 3 ( x ) + · · · + w 10 Φ 10 ( x ) � H 2 = such that: w 3 = w 4 = · · · = w 10 = 0 H 10 C → ∞ h ( x ) = w 0 + w 1 Φ 1 ( x ) + w 2 Φ 2 ( x ) + w 3 Φ 3 ( x ) + · · · + w 10 Φ 10 ( x ) q � w 2 q ≤ C H C = soft order constraint allows 10 ‘intermediate’ models տ � w 2 q =0 such that: q ≤ C budget for q =0 weights ր a ‘soft’ budget constraint on the sum of weights H 2 VC-perspective: H C is smaller than H 10 = ⇒ better generalization. � A M Regularization : 13 /30 � A M Regularization : 14 /30 c L Creator: Malik Magdon-Ismail H C − → c L Creator: Malik Magdon-Ismail Fitting data − → Fitting the Data Solving For w reg E in ( w ) = 1 min : N (Z w − y ) t (Z w − y ) The optimal weights w t w ≤ C subject to: w reg ∈ H C E in = const. ր regularized w lin should minimize the in-sample error, but be within the budget. Observations: normal 1. Optimal w tries to get as ‘close’ to w lin as possible. w Optimal w will use full budget and be on the surface w t w = C . 2. Surface w t w = C , at optimal w , should be perpindicular to ∇ E in . Otherwise can move along the surface and decrease E in . 3. Normal to surface w t w = C is the vector w . ∇ E in w reg is a solution to 4. Surface is ⊥ ∇ E in ; surface is ⊥ normal. ∇ E in is parallel to normal (but in opposite direction). w t w = C E in ( w ) = 1 min : N (Z w − y ) t (Z w − y ) w t w ≤ C subject to: ∇ E in ( w reg ) = − 2 λ C w reg ր λ C , the lagrange multiplier, is positive. The 2 is for mathematical convenience. � A c M Regularization : 15 /30 � A c M Regularization : 16 /30 L Creator: Malik Magdon-Ismail Getting w reg − → L Creator: Malik Magdon-Ismail Unconstrained minimization − →
Solving For w reg The Augmented Error Pick a C and minimize E in ( w ) is minimized, subject to: w t w ≤ C E in ( w ) subject to: w t w ≤ C � ⇔ ∇ E in ( w reg ) + 2 λ C w reg = 0 � ⇔ ∇ ( E in ( w ) + λ C w t w ) w = w reg = 0 � Pick a λ C and minimize E aug ( w ) = E in ( w ) + λ C w t w unconditionally տ ⇔ E in ( w ) + λ C w t w is minimized, unconditionally A penalty for the ‘complexity’ of h , measured by the size of the weights. We can pick any budget C . Translation: we are free to pick any multiplier λ C There is a correspondence: C ↑ λ C ↓ What’s the right C ? ↔ What’s the right λ C ? � A M Regularization : 17 /30 � A M Regularization : 18 /30 c L Creator: Malik Magdon-Ismail Augmented error − → c L Creator: Malik Magdon-Ismail Linear regression − → Linear Regression With Soft Order Constraint The Solution for w reg ∇ E aug ( w ) = 2Z t (Z w − y ) + 2 λ w E aug ( w ) = 1 N (Z w − y ) t (Z w − y ) + λ C w t w = 2(Z t Z + λ I) w − 2Z t y տ Convenient to set λ C = λ N Set ∇ E aug ( w ) = 0 E aug ( w ) = (Z w − y ) t (Z w − y ) + λ w t w տ N called ‘weight decay’ as the penalty encourages smaller weights w reg = (Z t Z + λ I) − 1 Z t y ↑ λ determines the amount of regularization Recall the unconstrained solution ( λ = 0): Unconditionally minimize E aug ( w ). w lin = (Z t Z) − 1 Z t y � A c M Regularization : 19 /30 � A c M Regularization : 20 /30 L Creator: Malik Magdon-Ismail Linear regression solution − → L Creator: Malik Magdon-Ismail Dramatic effect − →
A Little Regularization . . . . . . Goes A Long Way E in ( w ) + λ E in ( w ) + λ Minimizing N w t w with different λ ’s Minimizing N w t w with different λ ’s λ = 0 λ = 0 . 0001 λ = 0 λ = 0 . 0001 Data Data Target Target Fit Fit y y y x x x Overfitting Wow! Overfitting Wow! � A M Regularization : 21 /30 � A M Regularization : 22 /30 c L Creator: Malik Magdon-Ismail Just a little works − → c L Creator: Malik Magdon-Ismail Easy to overdose − → Don’t Overdose Overfitting and Underfitting E in ( w ) + λ N w t w Minimizing with different λ ’s 0.84 overfitting underfitting λ = 0 λ = 0 . 0001 λ = 0 . 01 λ = 1 Expected E out 0.8 Data Target Fit 0.76 y y y y 0 0.5 1 1.5 2 Regularization Parameter, λ x x x x → → Overfitting Underfitting � A c M Regularization : 23 /30 � A c M Regularization : 24 /30 L Creator: Malik Magdon-Ismail Overfitting and underfitting − → L Creator: Malik Magdon-Ismail Noise and regularization − →
Recommend
More recommend