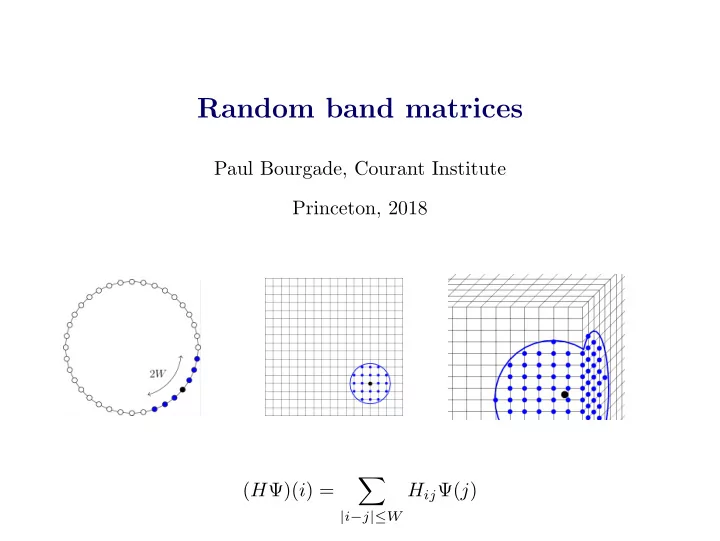
Random band matrices Paul Bourgade, Courant Institute Princeton, - PowerPoint PPT Presentation

Random band matrices Paul Bourgade, Courant Institute Princeton, 2018 � ( H Ψ)( i ) = H ij Ψ( j ) | i − j |≤ W

Integrable models : diagonal matrices ( W = 0) or the Gaussian Orthogonal Ensemble ( W = N/ 2, Gaussian entries), which satisfies : (i) Semicircle law as N → ∞ (Wigner) : � ρ ( E ) = 1 (4 − E 2 ) + . 2 π (ii) Eigenvalues locally converge (Gaudin, Mehta, Dyson) : � δ Nρ ( E )( λ k − E ) → Sine 1 . i (iii) Eigenvectors are uniform on the sphere, essentially supported on all sites (delocalization). The L´ evy-Borel law holds : for any � q � 2 = 1, √ N � u k , q � − N →∞ N (0 , 1) . →

For d = 1 , 2 , 3, vertices are elements of Λ = � 1 , N � d and H = ( H ij ) i,j ∈ Λ are centered, real, independent up to the symmetry H ij = H ji . Band width W : H ij = 0 if | i − j | > W. Localization (eigenvector support length ℓ ≪ N ) ? Conjecture : transition at some critical band width W c ( N ). Localization for W ≪ W c , delocalization for W ≫ W c , where  N 1 / 2 for d = 1 ( ℓ ∼ min( W 2 , N )) ,  for d = 2 ( ℓ ∼ min( e W 2 , N )) , (log N ) 1 / 2 W c =  O(1) for d = 3 . Simultaneous transition of eigenvalues statistics, from Poisson to GOE.

Context

Context Mean field models Band matrices Probabilistic QUE A spacially confined quantum mechanical system can only take certain discrete values of energy. Uranium-238 : These values are eigenvalues of a certain self-adjoint operator. The local spectral sta- Wigner’s universality idea. tistics of highly correlated quantum systems are given by the random matrix statistics of the same symmetry type. Random matrix statistics are ”universal” probabi- lity laws. Wigner’s vision is not proved for any realistic Hamiltonian. At least one model beyond mean-field ?

Context Mean field models Band matrices Probabilistic QUE Problem 1 : GOE and delocalization with no randomness. Bohigas-Giannoni-Schmit conjecture : if the billard is chaotic, GOE-type repulsion of eigenvalues. Helmholtz equation : − ∆ ψ n = λ n ψ n . area( D ) Weyl law : |{ i : λ i ≤ λ }| ∼ λ. 4 π λ →∞ Spacings statistics : � χ ( n ) = 1 δ area( D ) ( λ i +1 − λ i ) . 4 π n i ≤ n (Numerics : A. Backer) Delocalization on average (quantum ergodicity) is proved. GOE is not.

Context Mean field models Band matrices Probabilistic QUE Problem 2 : GOE and delocalization with non-trivial geometry. Anderson’s model for metal-insulator transition : H = − ∆ + λV ω on Z d ∩ [ − L, L ] d , random i.i.d. potential. Depending on λ and d , two distinct regimes : (i) Localization for large λ , any d , by multiscale analysis ( Frohlich-Spencer ), fractional moment ( Aizenman-Molchanov ). Poisson statistics ( Minami ). (ii) Delocalization and GOE (e.g., small λ for d = 3) ? For Anderson, localization was the new phenomenon. Mathematically speaking, delocalization is harder : for all dimensions, nothing is proved. Minami showed that Exponential decay of the resolvent implies Poisson statistics . Mechanism for GOE statistics in the delocalized phase ?

Context Mean field models Band matrices Probabilistic QUE Delocalization, GOE, for at least one model beyond mean-field ? Content : 1. Mean-field models. 2. Results for band matrices. 3. Elements of proof for the delocalized regime, d = 1 , W ≫ N 3 / 4 . Heuristics for transition exponents.

Mean field models

Context Mean field models Band matrices Probabilistic QUE Wigner matrices : eigenvalues universality. N × N symmetric, ij ) = 1 E ( H ij ) = 0 , E ( H 2 N , higher moments are finite but arbitrary . Theorem (2014) For any E ∈ ( − 2 , 2), � i δ Nρ ( E )( λ k − E ) → Sine 1 . Johansson (2000) : Hermitian case with large Gaussian component, HCIZ formula Erd˝ os-P´ ech´ e-Ramirez-Schlein-Yau (2009), Hermitian case, reverse heat flow Tao-Vu (2009) : Hermitian case, moment matching Erd˝ os-Schlein-Yau (2009) : general case with averaging over E , relative entropy method B.-Erd˝ os-Yau-Yin (2014) : general case, fixed energy, coupling method Erd˝ os-Schlein-Yau dynamic idea, use Dyson Brownian Motion : d H t = d B t − 1 √ 2 H t d t, H 0 Wigner . N

Context Mean field models Band matrices Probabilistic QUE Step 1 : relaxation. For t ≫ N − 1+ ε , local equilibrium is reached. Relies on coupled dynamics. Let x (0) be the spectrum of H 0 , y (0) of GOE. � � N d B i ( t ) + 1 2 1 d x i / d y i = d t. N x i /y i − x j /y j j � = i Then δ ℓ ( t ) = x ℓ ( t ) − y ℓ ( t ) satisfies the parabolic equation � δ k ( t ) − δ ℓ ( t ) ∂ t δ ℓ ( t ) = N ( x k ( t ) − x ℓ ( t ))( y k ( t ) − y ℓ ( t )) . k � = ℓ H¨ older regularity = universality. This coupling argument is local, it gives relaxation for any initial condition (Landon-Sosoe-Yau, Erd˝ os-Schnelli) . Step 2 : density. For t ≪ N − 1 2 − ε , the local eigenvalues distribution has almost not changed. Relies on the matrix structure (Itˆ o’s formula). This step fails for non mean field models.

Context Mean field models Band matrices Probabilistic QUE Wigner matrices : eigenvectors universality. Let u 1 , . . . , u N be the eigenvectors associated to λ 1 ≤ · · · ≤ λ N . By the density step, universality of bulk eigenvectors in the perturbative √ √ NH ij ) 3 ) = 0 , E (( NH ij ) 4 ) = 3 )( Knowles-Yin, Tao-Vu, 2011 ). setting E (( Theorem (B-Yau, 2013) √ For any deterministic k , q ∈ R N , N � q , u k � converges to a Gaussian. Relaxation step for eigenvectors ? Joint eigenvalues/eigenvectors dynamics (Bru, 1989) � d λ k = d B kk + 1 1 √ d t N λ k − λ ℓ N ℓ � = k � � 1 d B kℓ u ℓ − 1 d t d u k = √ ( λ k − λ ℓ ) 2 u k λ k − λ ℓ 2 N N ℓ � = k ℓ � = k

Context Mean field models Band matrices Probabilistic QUE Random walk in a dynamic random environment. Configuration η of n points on � 1 , N � . Usual notations : • η k , number of points at k • η ij configuration obtained by moving a point from i to j . √ Define z k ( t ) = N � q , u k ( t ) � and � N � � N � � � z 2 η k N 2 η k f ( η ) = f t, λ ( η ) = E | λ 0 →∞ / E . k k k =1 k =1 Lemma � f ( η ij ) − f ( η ) ∂ t f ( η ) = 2 η i (1+2 η j ) N ( λ i ( t ) − λ j ( t )) 2 . i � = j older regularity for t ≫ N − 1+ ε means moments are Gaussian. H¨

Context Mean field models Band matrices Probabilistic QUE Numerics : L. Benigni

Context Mean field models Band matrices Probabilistic QUE The dynamic approach applies beyond Wigner matrices. Examples : (i) Matrices with general mean, variance profile, summable decay of correlations (Ajanki-Erd˝ os-Kr¨ uger-Schr¨ oder, Che) (ii) Sparse random graphs of Erd˝ os-Renyi-type (Erd˝ os-Knowles-Yau-Yin, Lee-Schnelli, Huang-Landon-Yau) and d -regular models (Bauerschmidt-Huang-Knowles-Yau, B-Huang-Yau) (iii) Convolution, free probability model D 1 + U ∗ D 2 U , U uniform on O( N ) (Bao-Erd˝ os-Schnelli, Che-Landon) . The above matrix models are all mean-field.

Random band matrices

Context Mean field models Band matrices Probabilistic QUE We say that an eigenvector ψ is subexponentially localized at scale ℓ if there exists ε > 0, I ⊂ � 1 , N � , | I | ≤ ℓ , such that � α �∈ I | ψ ( α ) | 2 < e − N ε . Conjecture : W c = N 1 / 2 for d = 1 for bulk eigenvectors 1. Based on numerics (Casati-Molinari-Izrailev, 1990) 2. Theoretical evidence from supersymmetric method (Fyodorov-Mirlin, 1991) Corresponding localization length : ℓ ≈ W 2 . Analogy with the Anderson model H = − ∆ + λV ω : λ ≈ W − 1 . Consistent with localization length λ − 2 for d = 1, e λ − 2 for d = 2.

Context Mean field models Band matrices Probabilistic QUE Results on microscopic scale. 1. Edge behavior 2. Gaussian models with specific variance profile 3. Localization for general models 4. Delocalization for general models 1. Edge behavior. The transition at W ≈ N 5 / 6 was made rigorous by a subtle method of moments. Theorem (Sodin, 2010) 5 6 , then N 2 / 3 ( λ N − 2) converges to the Tracy-Widom If W ≫ N 5 6 , this does not hold. distribution. If W ≪ N

Context Mean field models Band matrices Probabilistic QUE 2. Gaussian models with specific variance profile, supersymmetry. Covariance structure E ( H ij H ℓk ) = 1 i = k,j = ℓ J ij where J ij = ( − W 2 ∆ + 1) − 1 ij . Essentially a 1 d band matrix of width W . Define F 2 ( E 1 , E 2 ) = E (det( E 1 − H ) det( E 2 − H )) . Theorem (Shcherbina-Shcherbina, 2014-2017) � � � if N ε < W < N 1 x x 2 − ε 1 ( D 2 ) − 1 F 2 E + Nρ ( E ) , E − → 2 + ε < W < N sin(2 πx ) 1 Nρ ( E ) if N 2 πx Proof idea : representation for the left hand side ( N = 2 n + 1) � n � det( X j − i∆ E e − W 2 − n Tr( X j + iΛ E � n − n +1 Tr( X j − X j − 1 ) 2 − 1 � n Nρ ( E ) 2 Λ x +i 2 )d X j , 2 2 2 − n where ∆ E = diag( E, E ), ∆ x = diag( x, − x ). Then steepest descent. Other results, 3 d density of states (Disertori-Pinson-Spencer) , 1 d pair correlation for W of order N (Shcherbina) .