
PHYSICAL ELECTRONICS(ECE3540) CHAPTER 6 – CARRIER GENERATION AND RECOMBINATION 1 Tennessee Technological University Wednesday, October 09, 2013
Chapter 6 – Carrier Generation and Recombination Chapter 4 : we considered the semiconductor in equilibrium and determined electron and hole concentrations in the conduction and valence bands, respectively. The net flow of the electrons and holes in a semiconductor will generate currents . The process by which these charged particles move is called transport . Chapter 5 : we considered the two basic transport mechanisms in a semiconductor crystal: drift the movement of charge due to electric fields, and diffusion the flow of charge due to density gradients. 2 Tennessee Technological University Wednesday, October 09, 2013
Chapter 6 – Carrier Generation and Recombination Chapter 6 : we will discuss the behavior of non-equilibrium electron and hole concentrations as functions of time and space. We will develop the ambi-polar transport equation which describes the behavior of the excess electrons and holes. We can define two new parameters that apply to the non-equilibrium semiconductor: the quasi- Fermi energy for electrons and the quasi-Fermi energy for holes. 3 Tennessee Technological University Wednesday, October 09, 2013
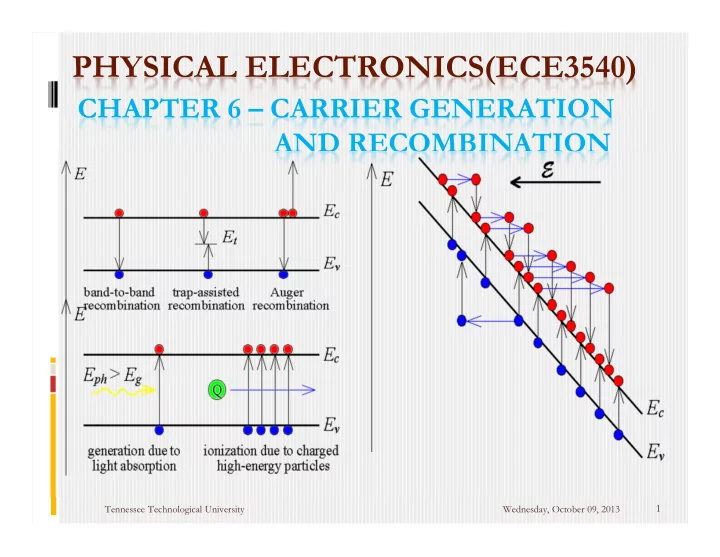
Carrier Generation and Recombination Generation: is the process whereby electrons and holes are created. Recombination: is the process whereby electrons and holes are annihilated. Any deviation from thermal equilibrium will tend to change the electron and hole concentrations in a semiconductor. Examples: A sudden increase in temperature will increase the rate at which electrons and holes are thermally generated so that their concentrations will change with time until new equilibrium values are reached. An external excitation, such as light (a flux of photons), can also generate electrons and holes, creating a non-equilibrium condition. 4 Tennessee Technological University Wednesday, October 09, 2013
The Semiconductor in Equilibrium Since the net carrier concentrations are independent of time in thermal equilibrium, the rate at which electrons and holes are generated and the rate at which they recombine must be equal. Let G n0 and G p0 be the thermal-generation rate of electrons and holes in #/cm 3 -s. For a direct band-to-band generation, the electrons and holes are created in pairs, therefore: G n0 = G p0 . 5 Tennessee Technological University Wednesday, October 09, 2013
The Semiconductor in Equilibrium - - Electron-Hole Electron-Hole Recombination Generation + X + Fig. 6.1: Electron-hole generation and recombination Let R n0 and R p0 be the recombination rates of electrons and holes, respectively, for a semiconductor in thermal equilibrium, again given in units of #/cm 3 -s. In direct band-to-band recombination, electrons and holes recombine in pairs, so that R n0 = R p0 . In thermal equilibrium, the concentrations of electrons and holes are independent of time; therefore, the generation and recombination rates are equal, so we have G n0 = G p0 = R n0 = R p0 6 Tennessee Technological University Wednesday, October 09, 2013
Excess Carrier Generation and Recombination Electrons in the valence band may be excited into the conduction band when, for example, high-energy photons are incident on a semiconductor. When this happens, not only is an electron created in the conduction band, but a hole is created in the valence band; thus an electron-hole pair is generated. The additional electrons and holes created are called excess electrons and excess holes. 7 Tennessee Technological University Wednesday, October 09, 2013
Excess Carrier Generation and Recombination The excess electrons and holes are generated by an external force at a particular rate. Let g n ’ be the generation rate of excess electrons and g p ’ be the generation rate of excess holes in units of #/cm 3 s For the direct band-to-band generation, the excess electrons and holes are also created in pairs, so we must have g n ’ = g p ’. When excess electrons and holes are created, the concentration of electrons in the conduction band and of holes in the valence band increase above their thermal equilibrium value. We may write n = n 0 + n and p = p 0 + p. n 0 and p 0 are the thermal-equilibrium concentrations, and n and p are the excess electron and hole concentrations. 8 Tennessee Technological University Wednesday, October 09, 2013
Excess Carrier Generation and Recombination Symbol Definition n o , p o Thermal equilibrium electron and hole concentration (independent of time and position) n, p Total electron and hole concentrations (may be functions of time and/or position) n = n – n 0 Excess electron concentration (may be function of time and/or position) p = p – p 0 Excess hole concentration (may be function of time and/or position) g n ’ , g p ’ Excess electron and hole generation rates. R n ’ , R p ’ Excess electron and hole recombination rates. n0 , p0 Excess minority carrier electron and hole lifetimes. Table. 6.1: Notations used in Carrier Generation and Recombination 9 Tennessee Technological University Wednesday, October 09, 2013
Excess Carrier Generation and Recombination A steady-state generation of excess electrons and holes will not cause a continual buildup of the carrier concentrations. As in the case of thermal equilibrium, an electron in the conduction band may "fall down" into the valence band, leading to the process of excess electron-hole recombination. The recombination rate for excess electrons is denoted by R n ’, and for excess holes by R p ’. Both parameters have units of #/cm3-s. The excess electrons and holes recombine in pairs, so the recombination rates must be equal. We can then write R n ’ = R p ’. In the direct band-to-band recombination that we are considering, the recombination occurs spontaneously: thus, the probability of an electron and hole recombining is constant with time. The rate at which electrons recombine must be proportional to the electron concentration and must also be proportional to the hole concentration. If there are no electrons or holes, there can be no recombination. 10 Tennessee Technological University Wednesday, October 09, 2013
Excess Carrier Generation and Recombination The net rate of change in the electron concentration can be written as: ( ) dn t 2 [ ( ) ( )] n n t p t r i (eq. 6.1) dt ( ) ( ) ( ) ( ) where n t n n t p t p p t 0 0 2 (eq. 6.1) is thermal-equilibrium generation rate. r n i Since excess electrons and holes are created and recombine in pairs, n(t) = p(t). (Excess electron and hole concentrations are equal and termed excess carriers.) The thermal-equilibrium parameters, n 0 and p 0 , independent of time, become: (eq. 6.2) ( ( )) d n t 2 [ ( ( ))( ( ))] ( )[( ) ( )] n n n t p p t n t n p n t 0 0 0 0 r i r dt 11 Tennessee Technological University Wednesday, October 09, 2013
Excess Carrier Generation and Recombination (Eq. 6.2) can easily be solved if we impose the condition of Low Level Injection. In an extrinsic n-type material, we generally have n o >> p o and, in an extrinsic p-type material, we generally have p o >>n o . Low-level injection means that the excess carrier concentration is much less than the thermal equilibrium majority carrier concentration. Conversely, high-level injection occurs when the excess carrier concentration becomes comparable to or greater than the thermal equilibrium majority carrier concentrations. If we consider a p-type material (p o >> n o ) under low-level injection ( n(t) <<p o ), then (eq. (6.2)) is: ( ( )) d n t (eq. (6.2) ( ) p n t 0 r dt 12 Tennessee Technological University Wednesday, October 09, 2013
Excess Carrier Generation and Recombination The solution to the equation is an exponential decay from the initial excess concentration, or (eq. 6.3) / ( ) ( 0 ) p t ( 0 ) t n t n e 0 n e 0 r n where n0 = ( r p 0 ) -1 and is a constant for the low-level injection. The above equation describes the decay of excess minority carrier electrons so that n0 is often referred to as the excess minority carrier lifetime. 13 Tennessee Technological University Wednesday, October 09, 2013
Recommend
More recommend