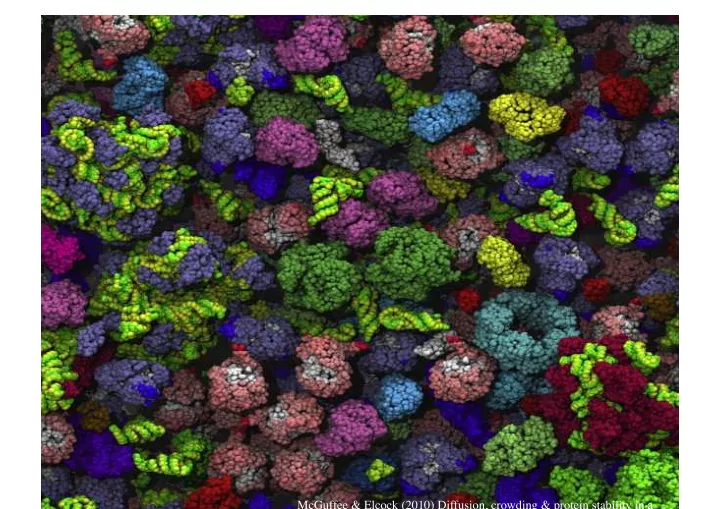
McGuffee & Elcock (2010) Diffusion, crowding & protein - PowerPoint PPT Presentation

McGuffee & Elcock (2010) Diffusion, crowding & protein stability in a

Macromolecular Crowding

Molecules and Complexes: E. coli Census • Nproteins ~ 3x10^6 • Nribosomes ~ 20,000 • Nlipids ~ 2x10^7 Spacing for a molecule of given concentration c: d = c − 1 3

Protein Spacing in E. coli • Estimate • Average protein-protein distance ~ 10 nm • 1 mM protein in vitro distance ~ 100 nm 1 um Radius of protein ~ 2nm

Linked Polymer Network Architecture Intenstinal microvilli Axon bundle Ligament collagen bundle Cellulose network of a plant cell Actin web in a miving cell Basement membrane Collagen fibrils Gram positive bacterial wall (atomic resolution)

• Effect on binding and interaction • Difference between cells and dilute solutions

Ten Commandments of Enzymology, Amended 1. Thou shalt rely on enzymology to resolve and reconstitute biologic events 2. Trust the universality of biochemistry and the power of microbiology (Escherichia sapiens) 3. Not believe something just because you can Arthur Kornberg Nobel Prize for Chemistry (1959) explain it Discovery of DNA polymerase (now known as DNA polymerase I) 4. Not waste clean thinking on dirty enzymes 5. Not waste clean enzymes on dirty substrates 6. Use genetics and genomics 7. Be aware that cells are molecularly crowded Be aware that cells are molecularly crowded 8. Depend on viruses to open windows 9. Remain mindful of the power of radioactive tracers 10. Employ enzymes as unique reagents Kornberg (2003) Tr. Biochem. Sci.

Fish Keratocyte Leading Edge Fish skin keratocyte Front edge: Ordered, Branched Membrane stripped platinum coated E.M. Middle zone: Randomly overlaid filaments

Cellular Effects of Crowding • Equilibrium binding • Diffusive processes

ATPase Rate 7.5% 5% 2.5% 0% PEG concentration T4 DNA polymerase clamp-loader proteins

Experimental Measures of Diffusivity Method 2 sizes BODIPY-FI FCS Method 3 Verkman (2002) TiBS Time Method 1 resolved Fluorescence Anisotropy

Cellular Diffusion Verkman (2002) TiBS Coefficients

Single Molecule GFP-Lck Imaging Membrane Proteins Lck Tyrosine kinase Jurkat T-cells TIRF microscopy Anti-T cell receptor Abs stimulate clustering Long distance Trapped Douglass & Vale (2005)

Membrane Microdomains CD2 Lck Merge T-cell Signalling domains in CD2-enriched signalling domains Signalling activated by antibody-patch on coverslip

Lipid Rafts GPI-anchored proteins Raft-associated lipids Mayor Lab, NCBS Bangalore

Lck GFP Effective Diffusion <d^2> = < [d(t)-d(t+ δ t)]^2 >, For different values of δ t. Raft targeted Lck-10 GFP Plotting d^2 vs δ t gives us a profile that can be fitted by <d^2>=2*D*t^ α α = 1 for normal diffusion Bacher, Reichenzeller, Athale et al. (2004) Klopfstein et al. (2002) Cell

TIRF: At the Surface Evanescent wave illumination with limited range Nikon Instruments

Lattice Model of Crowding Ω v = reaction volume L=ligand no. C=Crowding molec. no.

Ligand-Receptor Binding 1 p bound = ) e β Δ ε L ( 1 + Ω− L − C L b − ε L sol Δ ε L = ε L L << Ω When C increases, p bound increases

Crowding Changes L-R binding Probability

Dissociation Rate 7.5% 5% 2.5% 0% PEG concentration n ( ) [ ] K d L K d = 1 p bound = v e β Δ e n ( ) [ ] K d 1 + L v=volume of single lattice site Δε = binding energy Binding constant PEG dependent)

PEG as Crowdant T4 atpase data, PEG size (12 kDa) << Protein size (164 kDa) Ω large boxes r small boxes in each large box

Crowdant Smaller than Ligand

Binding 1 p bound = 1 + Ω L (1 − φ C ) r e B Δ ε L φ C = C r Ω Where, volume fraction of the crowding molecules in solution Assuming L << Ω And (N+r)!/N! ~ N r

Dissociation Constant K d = 1 v e β Δ e ( ) K d φ C r ( ) = 1 − φ C ( ) K d φ C = 0 Volume fraction dependent dissociation constant K d

Factors Affecting Crowding

Osmotic Pressure and Crowding Osmotic pressure due to excess Hemoglobin p = − k B T v ln(1 − [ H ] v ) p = pressure v=volume of single box in lattice [H]=concentration of Hb molecules=H/ Ω v

Crowding and Osmotic Pressure Free parameter is v V=5.8 nm Hard sphere gas model Experiment Lattice gas

Hard Sphere Gas Model Boltzmann 1899 p = k B T [ H ](1 + x + 0.625 x 2 + 0.287 x 3 + 0.11 x 4 ) Where x = 4V[H] V=volume of hard sphere

Next • Crowded polymers and ordering • Cytoskeleton • Motors • Cells in tissues • FRAP data • Paper presentations

2011-03-23

Macromolecular Crowding • 10-100% of fluid volume of cytoplasm lies within 1 molecular diameter of the surface of fibrous and membraneous structures • Pores • Reactant X and pore size comparable

Sieving Effect Verkman (2002) TiBS

Volume Exclusion Excluded volume Available volume Minton (2001) J. Biol. Chem.

Relative Sizes Minton (2001) J. Biol. Chem.

Volume Available ( ) ( ) = v tot v a , i γ i ≡ a i c i Effective and actual concentrations v tot =total volume v a,i =volume available to species i

Haemoglobin Concentration Normal RBC Concentration ~ 300gm/L

2011-03-29

Forces due to Volume Exclusion Large particle near surface Two large particles in solution Depletion forces Volume available to smaller molecules increases Two rod-like molecules in solution

Origin of Depletion Forces R= radius of large disk r = radius of small disk Surface 2D geometry Find area available to small disks, as a function of distance z between large disk and surface

Excluded Volume Interactions Area available to small disks R= radius of large disk z=distance between large disk and surface r = radius of small disk Surface 2D geometry Entropy increases

Free Energy Change No conventional forces- van der Walls, electrostatics, etc. Free energy change by change in entropy is:     G ex = − Nk B T ln V box − V ex  + Nk B T ln V box     v   v  V box = volume of box, V ex =excluded volume, v=volume of unit cell, N=no. of SMALL MOLECULE particles

Free Energy If V ex << V box , approximate ln(1+x) ≈ ln(x) G ex = Nk B T V ex V box If 2 large particles overlap excluded volumes, V ex increases entropy of small particle Nk B T ~ ideal gas (osmotic) pressure of small particles in box V bpx

Depeletion Force

Volume and Force V ex = 2 ⋅ 4 π 3 − V overlap ( ) R + r Total excluded volume 3 V sphericalcone = 2 π 2 ⋅ R + r − D 2 ( ) ( ) Volume of spherical cone R + r 3 V cone = π 2 − D 2 [ ] 2 ( ) ( ) 3 D 2 R + r Volume cone V overlap = 2 π 2 2 R + 2 r + D 2 Overlap ( ) ( ) R + r + D 2 3   2 − D 2 F depletion = − ∂ G ex ( ) ∂ D = − p π R + r   Depletion Force 4   p = nk B T , n=N/V box , and distance 2R<D<2(R+r)

Depletion Force Measurement 2 beads, DNA conc. R=625 nm, Move in DNA conc. line Depletion agent- DNA conc. Phage λ G ex ( D ) = pV overlap DNA r=500 nm p ( D ) ∝ e − β G ex ( D )

Entropic Ordering Rods: Filamentous viruses Spheres

Volume Exclusion Mutual exclusion v=volume occupied N=number of macromolecules Ω ! Z ex ( N ) = ( ) ! N ! Ω− N Ω =total number of boxes N=no. of macromolecules Z nex ( N ) = Ω N In absence of excluded volume N !

Free Energy for Excluded Volume Free energy G = − k B T ln Z Δ G ex = G ex − G nex = − k B T ln Z ex Z nex Using stirling’s approximation, and assuming Ω ≈ e − N Ω >> N, and ( ) 1 − N Ω N   Z ex ≈ 1 − N   Z nex   Ω  ≈ k B T N 2   Δ G ex = − Nk B T ln 1 − N    Ω Ω

Polymers, Crowding and RW Model • Random walk model ignores self-avoidance Na 2 • Size of macro-molecule like DNA ~ N=number of segments, a=persistence length Competing effects: • Entropy makes chain compact • Self-avoidance swells the chain

Random Walk Polymer G ( R ) = − TS RW ( R ) + G ex ( R ) Free energy R=radius of polymer S RW (R)=random walk entropy of chain of length R Entropy from probability distribution P(R;N) 3 R 2 S RW ( R ) = k B T ln P ( R ; N ) + const = − k B 2 Na 2 + const

Excluded volume • Assume polymer to be gas with hard cylinders of length a and diameter d • Mutual orientation angle θ decides excluded volume v = 2 da 2 sin θ

• For d<<a • Averaging sin( θ ) over all orientations gives π a 2 d estimate for excluded volume 2 G ex = k B TN φ • Free energy • Volume fraction of N hard cylinders 1 2 π a 2 d 2 π R 3 = N 3 a 2 d φ ( R ) = N 1 8 R 3

Free Energy Difference Δ G ex ≈ k B T N 2 • Since Ω = k B TN φ G ex ( R ) = k B TN 2 3 a 2 d 8 R 3 • Flory’s estimate of free energy of polymer G flory ( R ) = k B T 3 R 2 2 Na 2 + k B TN 2 3 a 2 d 8 R 3 1/ 5 • Size of chain   R flory = 3 8 a 4 d N 3/ 5    

RW vs. SAW • Power scaling RW (N 1/2 ), SAW (N 3/5 ) • Short polymers RW still valid 1 G ex = k B T 3 d S RW = 3 a N 2 2 k B T 8 For DNA d~2nm, a=100nm For N<<16(d/a)=40,000, G self avoid < RW entropy L=Na=40,000x100 nm (kuhn length) ~ 16 µ m

Protein Folding & Crowding Chaperones